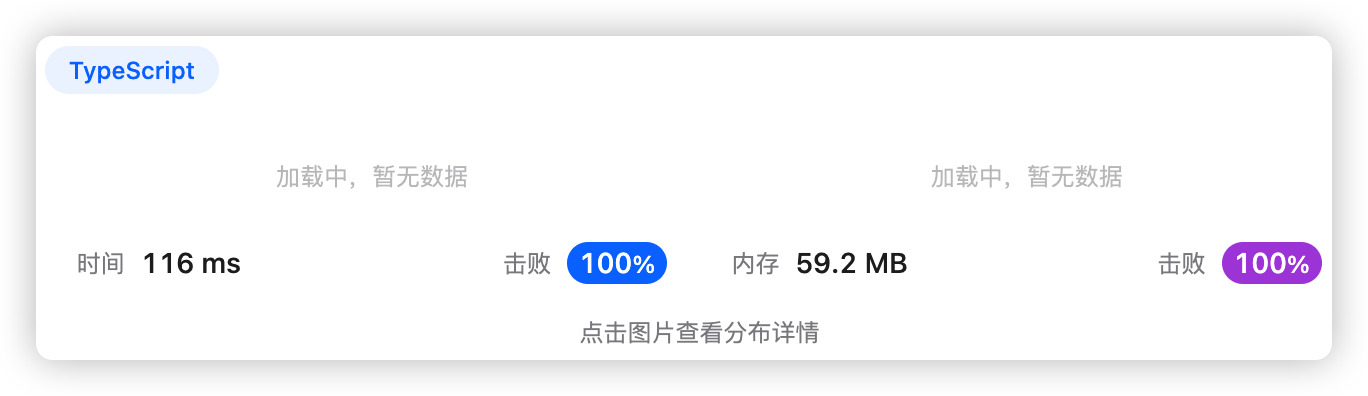
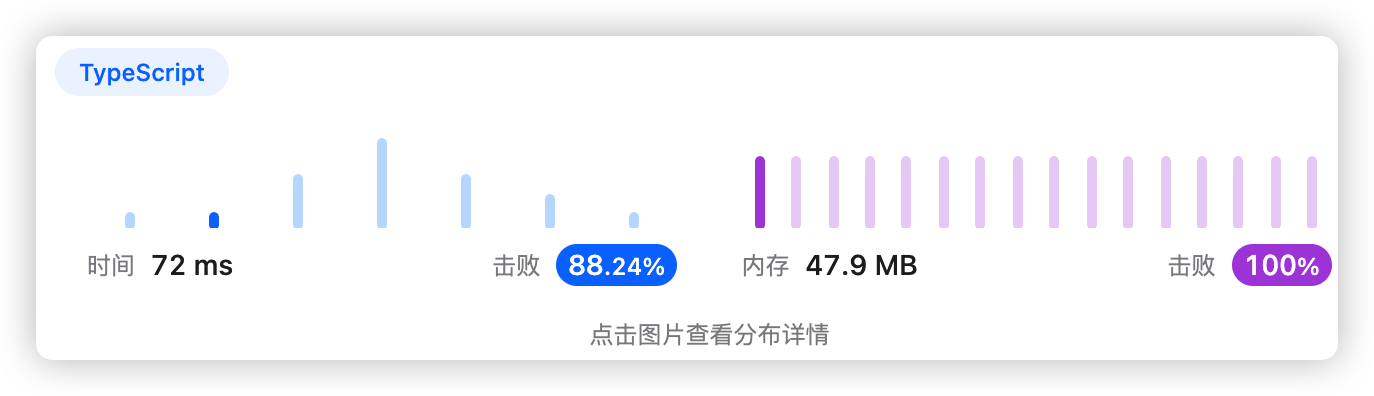
1、题干
给定一个二叉搜索树 root (BST),请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
提醒一下, 二叉搜索树 满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1:
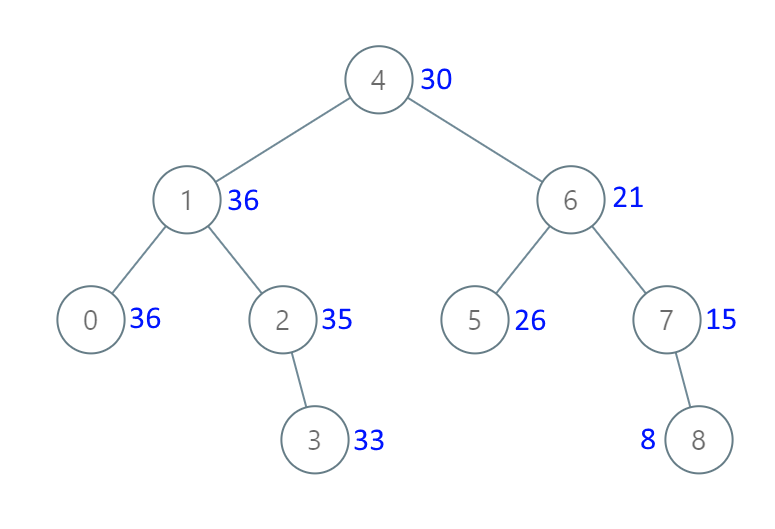
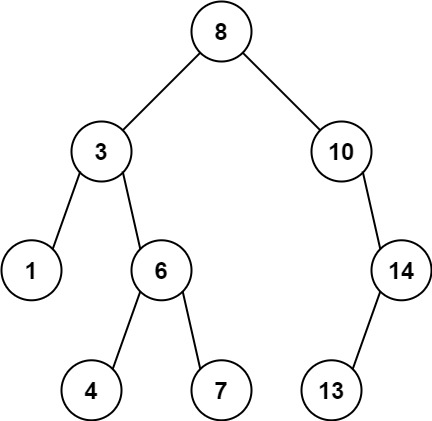
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
提示:
- 树中的节点数在
[1, 100]范围内。 0 <= Node.val <= 100- 树中的所有值均 不重复 。
注意:该题目与 538: https://leetcode-cn.com/problems/convert-bst-to-greater-tree/ 相同
2、思路
根据题意使用DFS模拟,需要注意:
- 对左子节点求和,需要将父节点求和结果、右子树节点之和、自身数值3者累加
- 对右子节点求和,需要将右边祖先节点求和结果、右子树节点之和、自身数值3者累加
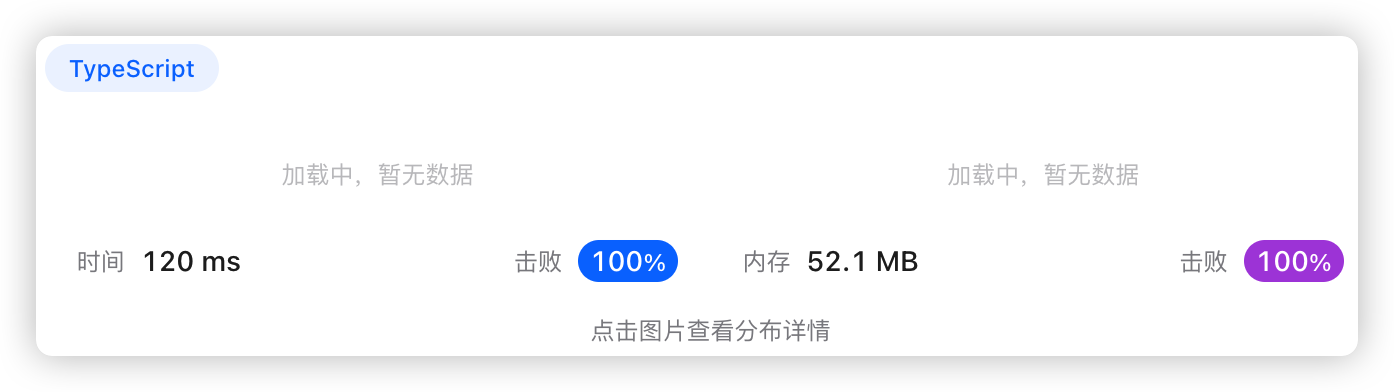
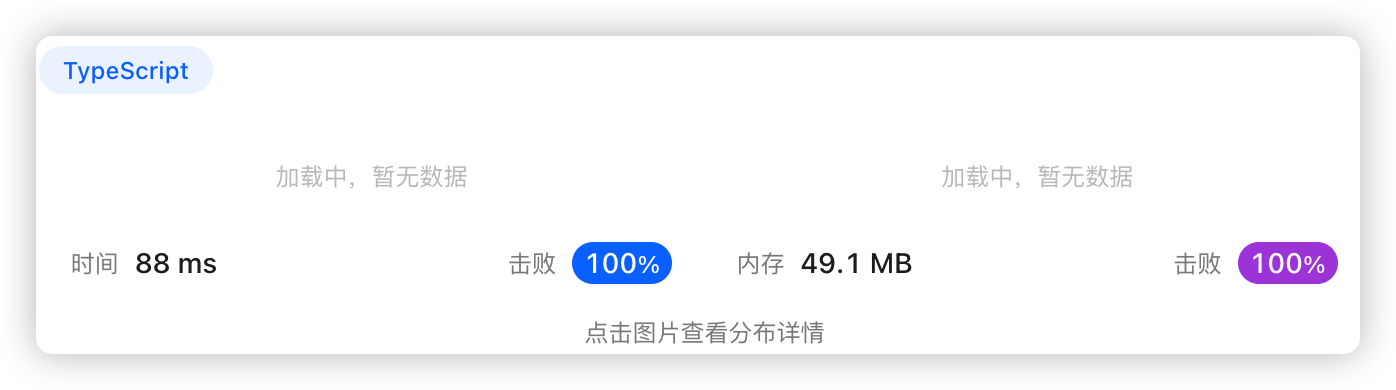
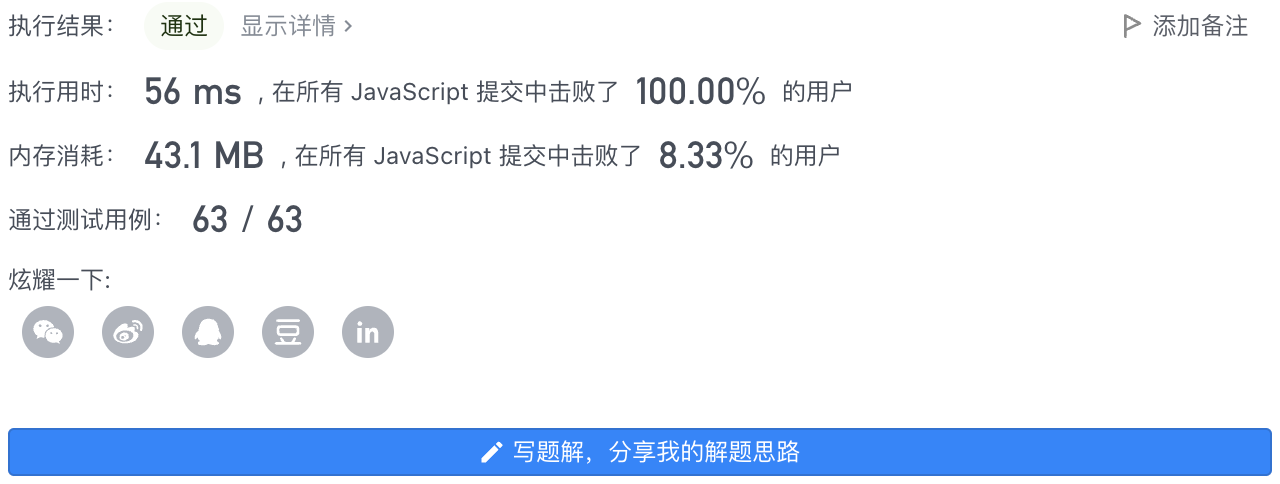
3、代码
function bstToGst(root: TreeNode | null): TreeNode | null {
return dfs(root), root;
}
function dfs(root?: TreeNode, pSum = 0): number {
if (!root) return 0;
const val = root.val;
const rSum = dfs(root.right, pSum);
root.val = val + pSum + rSum;
const lSum = dfs(root.left, root.val);
return val + rSum + lSum;
}