1、题干
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
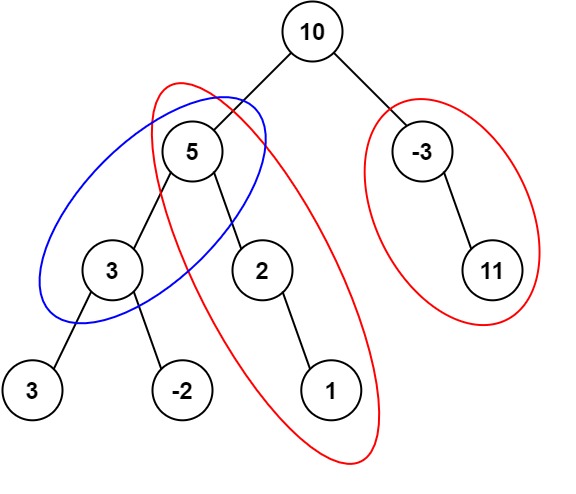
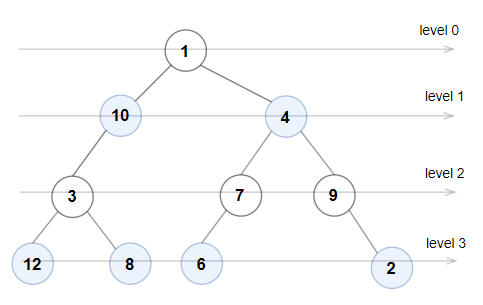
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
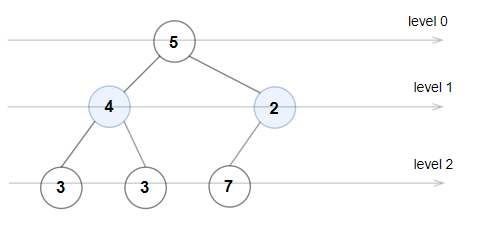
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:3
提示:
- 二叉树的节点个数的范围是
[0,1000] -109 <= Node.val <= 109-1000 <= targetSum <= 1000
注意:本题与主站 437 题相同:https://leetcode-cn.com/problems/path-sum-iii/
2、解法1
使用DFS递归遍历树的所有节点,递归函数接收上层传递下来的路径上所有前缀和,遍历所有前缀和并计算是否存在和等于targetSum的路径(计算公式node.val + sums[sums.length - 1] - (sums[i] || 0) === targetSum),存在则最终结果+1,时间复杂度为。
上述时间复杂度是估算值,因为每个节点需要访问一次,因此至少有的复杂度,另外每个节点内部需要再遍历前缀和数组,而数组长度最大为树的最大高度,因此综合估算时间复杂度为。
3、代码
var pathSum = function (root, targetSum) {
if (!root) return 0;
let res = root.val === targetSum ? 1 : 0;
function dfs(node, sums) {
if (!node) return;
for (let i = -1; i < sums.length; i++) {
if (node.val + sums[sums.length - 1] - (sums[i] || 0) === targetSum) res++;
}
dfs(node.left, [...sums, (sums[sums.length - 1] || 0) + node.val]);
dfs(node.right, [...sums, (sums[sums.length - 1] || 0) + node.val]);
}
return dfs(root, []), res;
};
4、执行结果
执行用时: 148 ms 内存消耗: 57.8 MB
5、解法2
该解法是解法1的优化版本,利用了哈希表存储前缀和,另外使用了回溯的思想重置前缀和状态,优化后的时间复杂度为。
- 同样使用DFS递归遍历树的所有节点,但使用
Map存储前缀和及其数量,递归时在Map中查找是否已存在等于sum - targetSum的路径前缀和,存在则最终结果累加其数量 - 将当前路径总和对应的数量累加1
- 然后进入下层递归,同样执行上述逻辑
- 下层递归结束时,将当前路径总和对应的数量累减1
6、代码
var pathSum = function (root, targetSum) {
if (!root) return 0;
let res = 0, map = new Map();
map.set(0, 1);
function dfs(node, sum) {
if (!node) return;
sum = sum + node.val;
res += map.get(sum - targetSum) || 0;
map.set(sum, (map.get(sum) || 0) + 1);
dfs(node.left, sum);
dfs(node.right, sum);
map.set(sum, map.get(sum) - 1);
}
return dfs(root, 0), res;
};
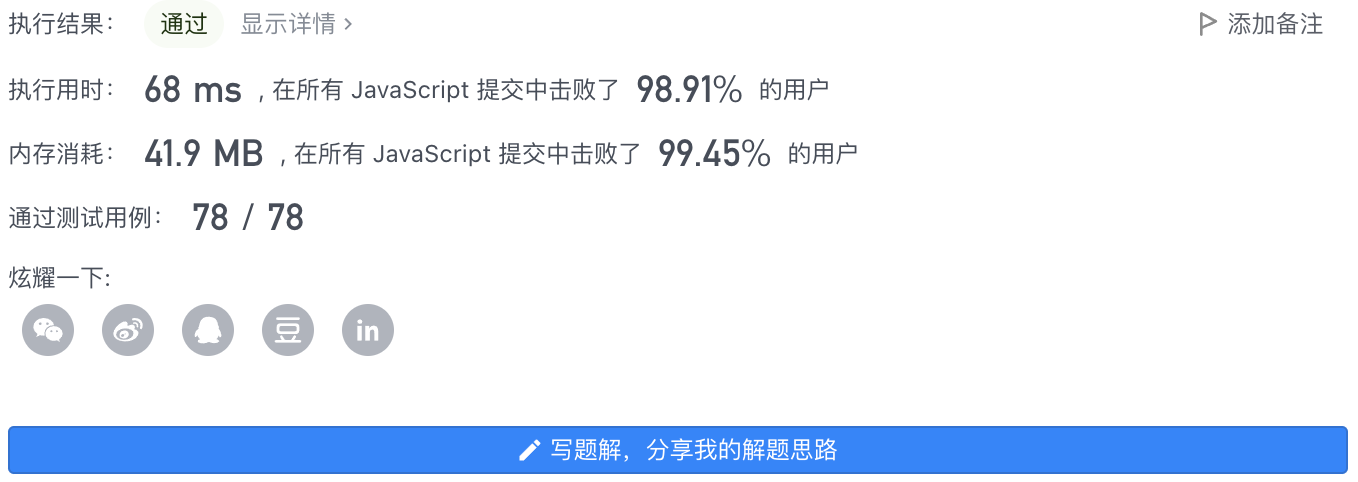
7、执行结果