1、题干
给你一棵二叉搜索树,请 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
示例 1:
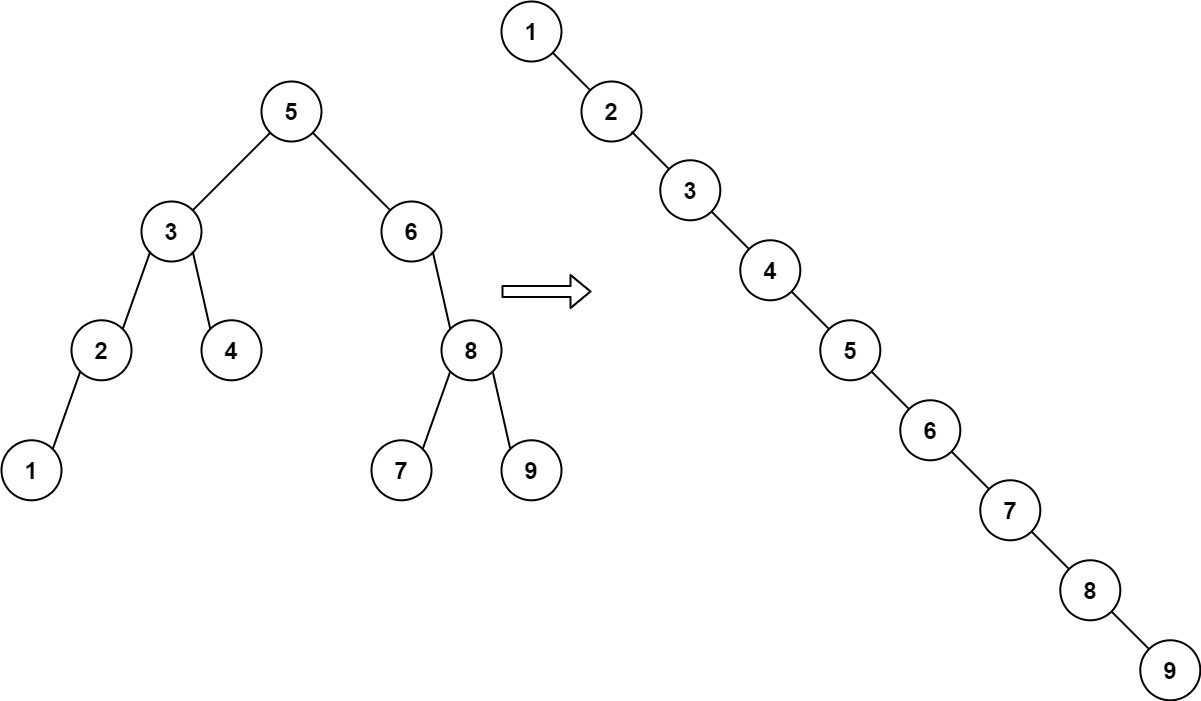
输入:root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
示例 2:
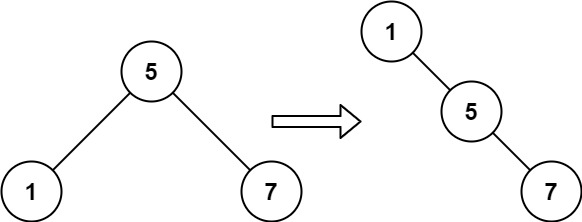
输入:root = [5,1,7]
输出:[1,null,5,null,7]
提示:
- 树中节点数的取值范围是
[1, 100] 0 <= Node.val <= 1000
注意:本题与主站 897 题相同: https://leetcode-cn.com/problems/increasing-order-search-tree/
2、解法1-DFS+改变指针
深度遍历所有节点,在递归左子节点后构造新的二叉树,newRoot用于记录新树的根节点,若newRoot为空则赋值为当前节点,lastNode用于记录新树的最后一个节点,若lastNode有值则将其右子节点置为当前节点,然后将lastNode置为当前节点,当前节点的左子节点置为空,最后返回newRoot
3、代码
var increasingBST = function (root) {
let newRoot = null, lastNode = null;
function dfs(node) {
if (!node) return;
dfs(node.left);
if (!newRoot) newRoot = node;
if (lastNode) lastNode.right = node;
lastNode = node;
node.left = null;
dfs(node.right);
}
dfs(root);
return newRoot;
};
4、执行结果

5、解法2-DFS+数组
深度遍历将节点按中序存入数组中,结束后对节点数组进行遍历,将当前节点的左子节点置空右子节点置为下一个数组元素,最后返回数组首个元素。
6、代码
var increasingBST = function (root) {
const arr = [];
function dfs(node) {
if (!node) return;
dfs(node.left);
arr.push(node);
dfs(node.right);
}
dfs(root);
for (let i = 0; i < arr.length; i++) {
arr[i].left = null;
arr[i].right = arr[i + 1] || null;
}
return arr[0];
};
7、执行结果
执行用时: 68 ms 内存消耗: 39.2 MB