3 篇博文 含有标签「数论」

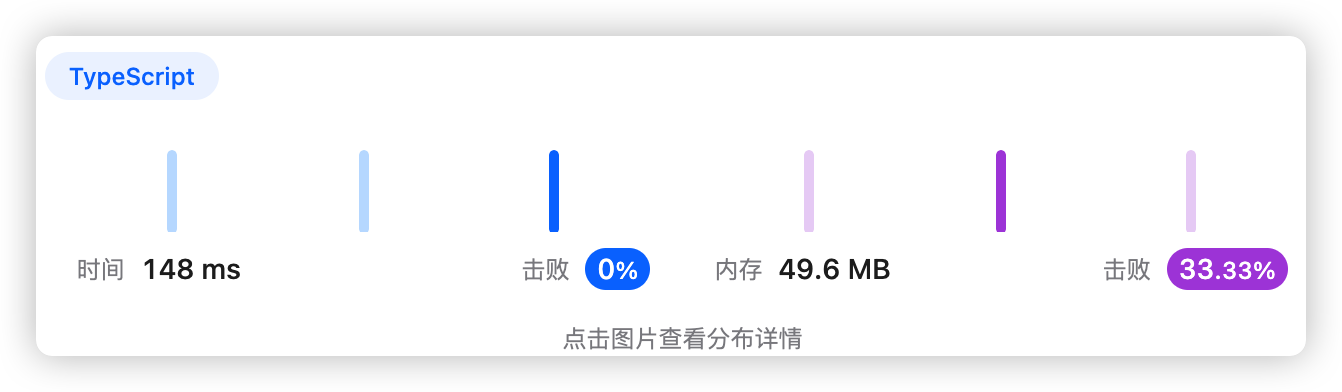
1、题干​

给你一个正整数数组 nums，你需要从中任选一些子集，然后将子集中每一个数乘以一个 任意整数，并求出他们的和。

假如该和结果为 1，那么原数组就是一个「好数组」，则返回 True；否则请返回 False。

示例 1：

输入：nums = [12,5,7,23]
输出：true
解释：挑选数字 5 和 7。
5*3 + 7*(-2) = 1

示例 2：

输入：nums = [29,6,10]
输出：true
解释：挑选数字 29, 6 和 10。
29*1 + 6*(-3) + 10*(-1) = 1

示例 3：

输入：nums = [3,6]
输出：false

提示：

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^9

2、思路​

这不是我能写出来的题，看了提示才AC

根据提示，要求所有数字的最大公约数是否等于1。想到的思路是：先升序排序 nums 数组，如果存在相邻数字的最大公约数 gi 等于1，或者 gi 与 gcd(nums[0],nums[1]) 的最大公约数等于1，那么 nums 是一个好数组。虽然过了，但无法证明算法正确性

3、代码​

function isGoodArray(nums: number[]): boolean {
    nums.sort((a, b) => a - b);
    const gcd = (a: number, b: number) => a ? gcd(b % a, a) : b;

    const g1 = gcd(nums[0], nums[1] || 0);

    for (let i = 1; i < nums.length; i++) {
        const gi = gcd(nums[i], nums[i + 1]);
        if (gi === 1 || gcd(g1, gi) === 1) return true;
    }

    return g1 === 1;
};

官解根据裴蜀定理推论和证明，严谨很多，代码也不难。整体思路也是求所有数字的最大公约数是否等于1

function isGoodArray(nums: number[]): boolean {
    let d = nums[0];
    const gcd = (a: number, b: number) => a ? gcd(b % a, a) : b;

    for (let i = 0; i < nums.length && d !== 1; i++) {
        d = gcd(d, nums[i]);
    }

    return d === 1;
};

4、复杂度​

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(logn)$

5、执行结果​

1、题干​

给你一个由正整数组成的数组 nums 。

数字序列的 最大公约数 定义为序列中所有整数的共有约数中的最大整数。

• 例如，序列 [4,6,16] 的最大公约数是 2 。

数组的一个 子序列 本质是一个序列，可以通过删除数组中的某些元素（或者不删除）得到。

• 例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。

计算并返回 nums 的所有 非空 子序列中 不同 最大公约数的 数目 。

示例 1：

输入：nums = [6,10,3]
输出：5
解释：上图显示了所有的非空子序列与各自的最大公约数。
不同的最大公约数为 6 、10 、3 、2 和 1 。

示例 2：

输入：nums = [5,15,40,5,6]
输出：7

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 2 * 105

题目太难，看了题解才写出来。

2、思路​

所有最大公约数都处于 $[1,max(nums)]$ 范围内，因此可以枚举该范围内的所有数字 i，判断该数字是否属于 nums 子序列的最大公约数。

具体判断时对 i 倍乘，若倍乘的数同时属于 nums 则求其最大公约数 g，g === i 则结果累加1。

3、代码​

function countDifferentSubsequenceGCDs(nums: number[]): number {
    let max = 0;
    for (const n of nums) max = n > max ? n : max;

    const set = new Array(max + 1);
    for (const n of nums) set[n] = 1;

    const gcd = (x: number, y: number) => y ? gcd(y, x % y) : x;

    let ans = 0;
    for (let i = 1; i <= max; i++) {
        if (set[i]) {
            ans++;
            continue;
        }

        let g = 0;
        for (let j = 2 * i; j <= max && g !== i; j += i) {
            if (set[j]) g = gcd(j, g);
        }

        if (g === i) ans++;
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n*logn)$
• 空间复杂度：$O(n)$

5、执行结果​

1、题干​

给你一个整数 n ，请你返回所有 0 到 1 之间（不包括 0 和 1）满足分母小于等于  n 的 最简 分数 。分数可以以 任意 顺序返回。

示例 1：

输入：n = 2
输出：["1/2"]
解释："1/2" 是唯一一个分母小于等于 2 的最简分数。

示例 2：

输入：n = 3
输出：["1/2","1/3","2/3"]

示例 3：

输入：n = 4
输出：["1/2","1/3","1/4","2/3","3/4"]
解释："2/4" 不是最简分数，因为它可以化简为 "1/2" 。

示例 4：

输入：n = 1
输出：[]

提示：

• 1 <= n <= 100

2、解法1-哈希表​

用哈希映射存储小数和分数字符串，其中小数作为键分数字符串作为值，最后返回哈希映射中的所有值

3、代码​

var simplifiedFractions = function (n) {
    const map = new Map();
    for (let i = 1; i < n; i++) {
        for (let j = i + 1; j <= n; j++) {
            if (!map.has(i / j)) map.set(i / j, `${i}/${j}`);
        }
    }

    return [...map.values()];
};

4、复杂度​

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

5、执行结果​

• 执行用时: 108 ms
• 内存消耗: 46.3 MB

6、解法2-求公约数​

参考求素数的方法，从 $2$ 开始遍历到 $\sqrt{n}$，看分子分母是否存在公约数

7、代码​

var simplifiedFractions = function (n) {
    function skip(min, max) {
        for (let i = 2; i * i <= max; i++) {
            if (max % i === 0 && (min % i === 0 || min % (max / i) === 0)) return true;
        }
        return false;
    }

    const res = [];
    for (let i = 1; i < n; i++) {
        for (let j = i + 1; j <= n; j++) {
            if (!skip(i, j)) res.push(i + '/' + j);
        }
    }

    return res;
};

8、复杂度​

• 时间复杂度：$O(n^2*\sqrt{n})$
• 空间复杂度：$O(n)$

9、执行结果​

• 执行用时: 88 ms
• 内存消耗: 47.2 MB

10、解法3-分母因数倍乘+哈希集合​

参考求素数的方法，从 $2$ 开始遍历到 $\sqrt{n}$，求出所有小于分母的因数及其倍乘结果并存储到哈希集合 cdSet 中，若分子存在于 cdSet 中则说明分子分母存在公约数

11、代码​

var simplifiedFractions = function (n) {
    const res = [];
    for (let i = 2; i <= n; i++) {
        const cdSet = new Set();
        for (let c = 2; c * c <= i; c++) {
            if (i % c) continue;
            for (let m = 1; m * c < i; m++) {
                cdSet.add(m * c);
                if (m * i / c < i) cdSet.add(m * i / c);
            }
        }

        for (let j = 1; j < i; j++) {
            if (!cdSet.has(j)) res.push(j + '/' + i);
        }
    }

    return res;
};

12、复杂度​

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

13、执行结果​

• 执行用时: 84 ms
• 内存消耗: 46.9 MB