131 篇博文 含有标签「数组」

1、题干​

力扣公司的员工都使用员工卡来开办公室的门。每当一个员工使用一次他的员工卡，安保系统会记录下员工的名字和使用时间。如果一个员工在一小时时间内使用员工卡的次数大于等于三次，这个系统会自动发布一个 警告 。

给你字符串数组 keyName 和 keyTime ，其中 [keyName[i], keyTime[i]] 对应一个人的名字和他在 某一天 内使用员工卡的时间。

使用时间的格式是 24小时制 ，形如 "HH:MM" ，比方说 "23:51" 和 "09:49" 。

请你返回去重后的收到系统警告的员工名字，将它们按 字典序升序 排序后返回。

请注意 "10:00" - "11:00" 视为一个小时时间范围内，而 "22:51" - "23:52" 不被视为一小时时间范围内。

示例 1：

输入：keyName = ["daniel","daniel","daniel","luis","luis","luis","luis"], keyTime = ["10:00","10:40","11:00","09:00","11:00","13:00","15:00"]
输出：["daniel"]
解释："daniel" 在一小时内使用了 3 次员工卡（"10:00"，"10:40"，"11:00"）。

示例 2：

输入：keyName = ["alice","alice","alice","bob","bob","bob","bob"], keyTime = ["12:01","12:00","18:00","21:00","21:20","21:30","23:00"]
输出：["bob"]
解释："bob" 在一小时内使用了 3 次员工卡（"21:00"，"21:20"，"21:30"）。

提示：

• 1 <= keyName.length, keyTime.length <= 105
• keyName.length == keyTime.length
• keyTime 格式为 "HH:MM" 。
• 保证 [keyName[i], keyTime[i]] 形成的二元对 互不相同 。
• 1 <= keyName[i].length <= 10
• keyName[i] 只包含小写英文字母。

2、思路1​

哈希表存储员工姓名（键）和开门时间数组（值），时间转为分钟数并排序，最后检查每个员工的开门时间是否违规

3、代码​

function alertNames(names: string[], times: string[]): string[] {
    const map = new Map<string, number[]>();
    for (let i = 0; i < names.length; i++) {
        if (!map.has(names[i])) map.set(names[i], []);
        map.get(names[i]).push(60 * (+times[i].slice(0, 2)) + +(times[i].slice(3)));
    }

    const ans = [];
    for (const [name, minutes] of map) {
        if (minutes.length < 3) continue;

        minutes.sort((a, b) => a - b);
        for (let i = 0; i < minutes.length - 2 && ans.at(-1) !== name; i++) {
            if (minutes[i + 2] - minutes[i] <= 60) ans.push(name);
        }
    }

    return ans.sort();
};

4、复杂度​

• 时间复杂度：$O(n*logn)$
• 空间复杂度：$O(n)$

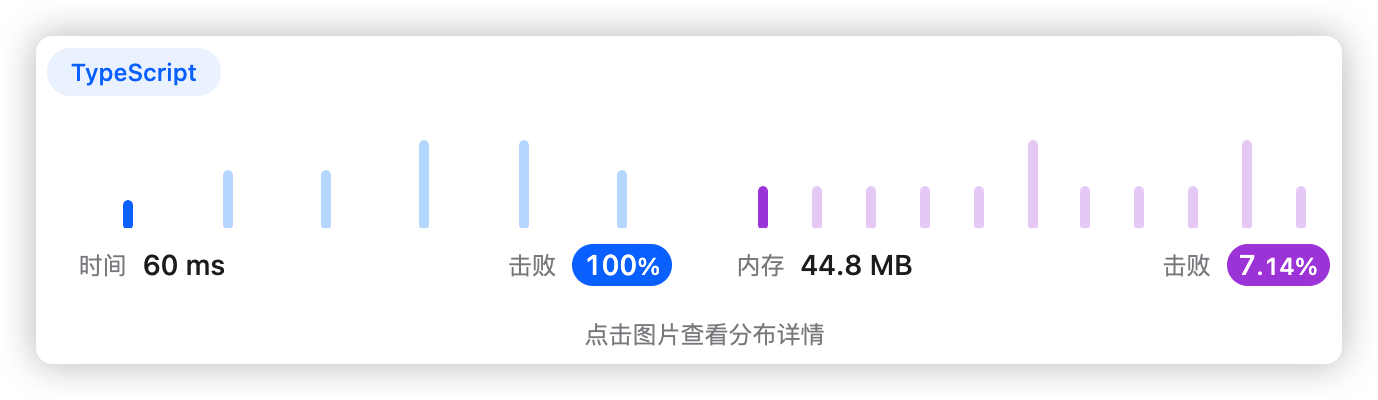
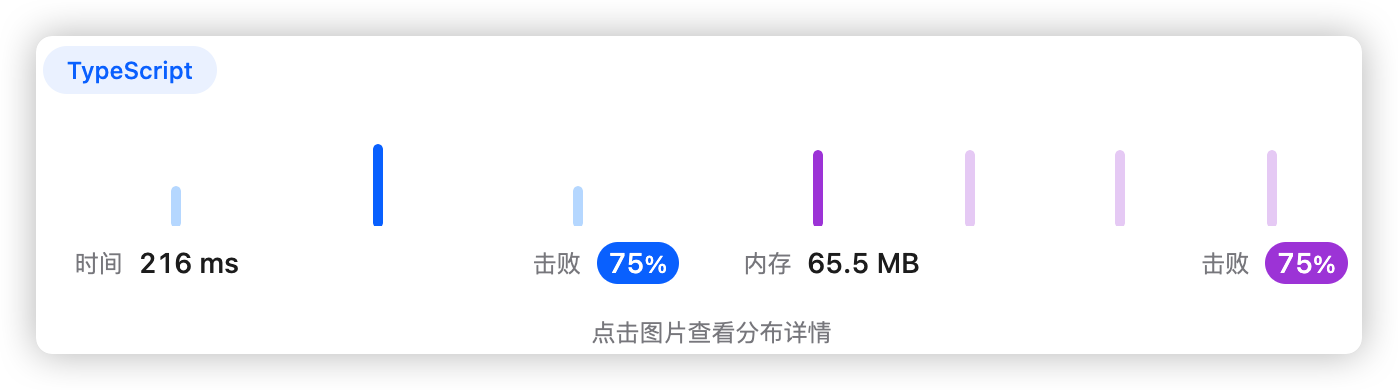
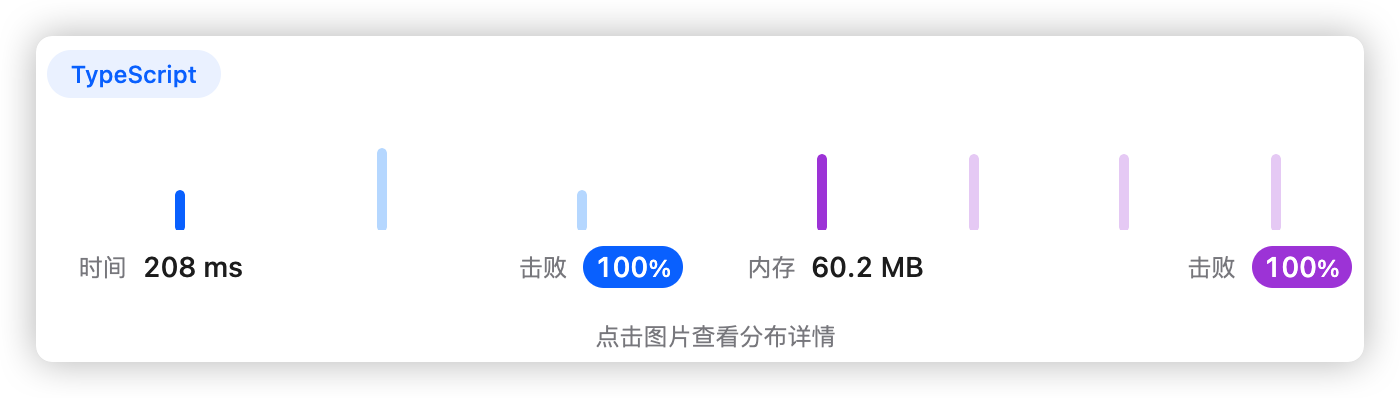
5、执行结果​

6、思路2​

二维数组存储员工姓名和开门时间，时间转为分钟数，对二维数组按姓名和分钟数升序排序，最后检查每个员工的开门时间是否违规

7、代码​

function alertNames(names: string[], times: string[]): string[] {
    const matrix: [string, number][] = names.map((n, i) => [n, 60 * (+times[i].slice(0, 2)) + +(times[i].slice(3))]);
    matrix.sort((a, b) => {
        if (a[0] === b[0]) return a[1] - b[1];
        return a[0] > b[0] ? 1 : -1;
    });

    const ans = [];

    for (let i = 0; i < matrix.length - 2; i++) {
        if (matrix[i + 2][0] !== matrix[i][0] || matrix[i][0] === ans.at(-1)) continue;
        if (matrix[i + 2][1] - matrix[i][1] <= 60) ans.push(matrix[i][0]);
    }

    return ans;
};

8、复杂度​

• 时间复杂度：$O(n*logn)$
• 空间复杂度：$O(n)$

9、执行结果​

1、题干​

你还记得那条风靡全球的贪吃蛇吗？

我们在一个 n*n 的网格上构建了新的迷宫地图，蛇的长度为 2，也就是说它会占去两个单元格。蛇会从左上角（(0, 0) 和 (0, 1)）开始移动。我们用 0 表示空单元格，用 1 表示障碍物。蛇需要移动到迷宫的右下角（(n-1, n-2) 和 (n-1, n-1)）。

每次移动，蛇可以这样走：

• 如果没有障碍，则向右移动一个单元格。并仍然保持身体的水平／竖直状态。
• 如果没有障碍，则向下移动一个单元格。并仍然保持身体的水平／竖直状态。
• 如果它处于水平状态并且其下面的两个单元都是空的，就顺时针旋转 90 度。蛇从（(r, c)、(r, c+1)）移动到 （(r, c)、(r+1, c)）。
  
• 如果它处于竖直状态并且其右面的两个单元都是空的，就逆时针旋转 90 度。蛇从（(r, c)、(r+1, c)）移动到（(r, c)、(r, c+1)）。
  

返回蛇抵达目的地所需的最少移动次数。

如果无法到达目的地，请返回 -1。

示例 1：

输入：grid = [[0,0,0,0,0,1],
               [1,1,0,0,1,0],
               [0,0,0,0,1,1],
               [0,0,1,0,1,0],
               [0,1,1,0,0,0],
               [0,1,1,0,0,0]]
输出：11
解释：
一种可能的解决方案是 [右, 右, 顺时针旋转, 右, 下, 下, 下, 下, 逆时针旋转, 右, 下]。

示例 2：

输入：grid = [[0,0,1,1,1,1],
               [0,0,0,0,1,1],
               [1,1,0,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,0]]
输出：9

提示：

• 2 <= n <= 100
• 0 <= grid[i][j] <= 1
• 蛇保证从空单元格开始出发。

2、思路​

使用 BFS 模拟，模拟过程使用二维矩阵存储访问状态，访问状态使用二进制表示：0未访问，1水平访问，2垂直访问，3水平访问+垂直访问

3、代码​

function minimumMoves(grid: number[][]): number {
    const n = grid.length;
    const dirs = [[0, 0], [0, 1], [1, 0], [1, 1]];
    const visited = grid.map(g => g.map(() => 0));

    function validate([r1, c1, r2, c2]: number[]) {
        const s = r1 === r2 ? 1 : 2;
        return grid[r1]?.at(c1) === 0 && grid[r2]?.at(c2) === 0 && (visited[r1][c1] | s) !== visited[r1][c1];
    }

    for (let step = 0, queue = [[0, 0, 0, 1]]; queue.length; step++) {
        const nextQueue = [];
        for (const [r1, c1, r2, c2] of queue) {
            if (r1 === n - 1 && r2 === n - 1 && c1 === n - 2 && c2 === n - 1) return step;

            const s = r1 === r2 ? 1 : 2;
            if ((visited[r1][c1] | s) === visited[r1][c1]) continue;

            visited[r1][c1] = visited[r1][c1] | s;

            // 水平：向右直走、向下平移
            // 垂直：向下直走、向右平移
            const p1 = [r1, c1 + 1, r2, c2 + 1], p2 = [r1 + 1, c1, r2 + 1, c2];
            if (validate(p1)) nextQueue.push(p1);
            if (validate(p2)) nextQueue.push(p2);

            // 旋转：必须满足4宫格为0
            if (!dirs.every(([dr, dc]) => grid[r1 + dr]?.at(c1 + dc) === 0)) continue;

            // 水平：顺时针旋转
            const p3 = [r1, c1, r2 + 1, c2 - 1];
            if (r1 === r2 && validate(p3)) nextQueue.push(p3);

            // 垂直：逆时针旋转
            const p4 = [r1, c1, r2 - 1, c2 + 1];
            if (c1 === c2 && validate(p4)) nextQueue.push(p4);
        }

        queue = nextQueue;
    }

    return -1;
};

4、复杂度​

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n^2)$

5、执行结果​

1、题干​

给你一个长度为 n 的整数数组 coins ，它代表你拥有的 n 个硬币。第 i 个硬币的值为 coins[i] 。如果你从这些硬币中选出一部分硬币，它们的和为 x ，那么称，你可以 构造 出 x 。

请返回从 0 开始（包括 0 ），你最多能 构造 出多少个连续整数。

你可能有多个相同值的硬币。

示例 1：

输入：coins = [1,3]
输出：2
解释：你可以得到以下这些值：
- 0：什么都不取 []
- 1：取 [1]
从 0 开始，你可以构造出 2 个连续整数。

示例 2：

输入：coins = [1,1,1,4]
输出：8
解释：你可以得到以下这些值：
- 0：什么都不取 []
- 1：取 [1]
- 2：取 [1,1]
- 3：取 [1,1,1]
- 4：取 [4]
- 5：取 [4,1]
- 6：取 [4,1,1]
- 7：取 [4,1,1,1]
从 0 开始，你可以构造出 8 个连续整数。

示例 3：

输入：nums = [1,4,10,3,1]
输出：20

提示：

• coins.length == n
• 1 <= n <= 4 * 104
• 1 <= coins[i] <= 4 * 104

2、思路​

按递增顺序逐个使用硬币 c 与当前的 x 构造出下一个 x 的范围 $[min(c,x) , x+c]$；若 c > x+1 则表示从该硬币开始无法构造连续整数；最后结果返回 x+1

注意：这个算法中硬币不能重复使用

3、代码​

function getMaximumConsecutive(coins: number[]): number {
    coins.sort((a, b) => a - b);

    let x = 0;
    for (const c of coins) {
        if (c <= x + 1) x = x + c;
    }

    return x + 1;
};

4、复杂度​

• 时间复杂度：$O(n*logn)$
• 空间复杂度：$O(logn)$

5、执行结果​

1、题干​

如果一个正方形矩阵满足下述 全部 条件，则称之为一个 X 矩阵 ：

1. 矩阵对角线上的所有元素都 不是 0
2. 矩阵中所有其他元素都是 0

给你一个大小为 n x n 的二维整数数组 grid ，表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ，返回 true ；否则，返回 false 。

示例 1：

输入：grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出：true
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 是一个 X 矩阵。

示例 2：

输入：grid = [[5,7,0],[0,3,1],[0,5,0]]
输出：false
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 不是一个 X 矩阵。

提示：

• n == grid.length == grid[i].length
• 3 <= n <= 100
• 0 <= grid[i][j] <= 105

2、思路​

遍历矩阵，对于矩阵中任意元素存在两个布尔状态 是否对角线 与 是否非0，二者不一致时返回 false，全部一致返回 true

3、代码​

function checkXMatrix(grid: number[][]): boolean {
    for (let i = 0; i < grid.length; i++) {
        for (let j = 0; j < grid[0].length; j++) {
            if ((i === j || i + j === grid.length - 1) !== !!grid[i][j]) return false;
        }
    }

    return true;
};

4、复杂度​

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

5、执行结果​

1、题干​

给你一个整数数组 nums 。你需要选择 恰好 一个下标（下标从 0 开始）并删除对应的元素。请注意剩下元素的下标可能会因为删除操作而发生改变。

比方说，如果 nums = [6,1,7,4,1] ，那么：

• 选择删除下标 1 ，剩下的数组为 nums = [6,7,4,1] 。
• 选择删除下标 2 ，剩下的数组为 nums = [6,1,4,1] 。
• 选择删除下标 4 ，剩下的数组为 nums = [6,1,7,4] 。

如果一个数组满足奇数下标元素的和与偶数下标元素的和相等，该数组就是一个 平衡数组 。

请你返回删除操作后，剩下的数组 nums 是 平衡数组 的 方案数 。

示例 1：

输入：nums = [2,1,6,4]
输出：1
解释：
删除下标 0 ：[1,6,4] -> 偶数元素下标为：1 + 4 = 5 。奇数元素下标为：6 。不平衡。
删除下标 1 ：[2,6,4] -> 偶数元素下标为：2 + 4 = 6 。奇数元素下标为：6 。平衡。
删除下标 2 ：[2,1,4] -> 偶数元素下标为：2 + 4 = 6 。奇数元素下标为：1 。不平衡。
删除下标 3 ：[2,1,6] -> 偶数元素下标为：2 + 6 = 8 。奇数元素下标为：1 。不平衡。
只有一种让剩余数组成为平衡数组的方案。

示例 2：

输入：nums = [1,1,1]
输出：3
解释：你可以删除任意元素，剩余数组都是平衡数组。

示例 3：

输入：nums = [1,2,3]
输出：0
解释：不管删除哪个元素，剩下数组都不是平衡数组。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 104

2、思路​

前缀和模拟

3、代码​

function waysToMakeFair(nums: number[]): number {
    let oddSum = 0, evenSum = 0;
    const sums = new Array(nums.length).fill(0);
    for (let i = 0; i < nums.length; i++) {
        sums[i] = i % 2 ? oddSum += nums[i] : evenSum += nums[i];
    }

    let ans = 0;
    const oddTail = !!((nums.length - 1) % 2);

    for (let i = 0; i < nums.length; i++) {
        const os1 = (i % 2 ? sums[i] : sums[i - 1]) || 0;
        const es1 = (i % 2 ? sums[i - 1] : sums[i]) || 0;

        const os2 = (sums.at(oddTail ? -2 : -1) || 0) - es1;
        const es2 = (sums.at(oddTail ? -1 : -2) || 0) - os1;

        if (i % 2 === 1 && os1 + os2 - nums[i] === es1 + es2) ans++;
        else if (i % 2 === 0 && os1 + os2 === es1 + es2 - nums[i]) ans++;
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

5、执行结果​

1、题干​

给你用户在 LeetCode 的操作日志，和一个整数 k 。日志用一个二维整数数组 logs 表示，其中每个 logs[i] = [IDi, timei] 表示 ID 为 IDi 的用户在 timei 分钟时执行了某个操作。

多个用户 可以同时执行操作，单个用户可以在同一分钟内执行 多个操作 。

指定用户的 用户活跃分钟数（user active minutes，UAM） 定义为用户对 LeetCode 执行操作的 唯一分钟数 。 即使一分钟内执行多个操作，也只能按一分钟计数。

请你统计用户活跃分钟数的分布情况，统计结果是一个长度为 k 且 下标从 1 开始计数 的数组 answer ，对于每个 j（1 <= j <= k），answer[j] 表示 用户活跃分钟数 等于 j 的用户数。

返回上面描述的答案数组 answer 。

示例 1：

输入：logs = [[0,5],[1,2],[0,2],[0,5],[1,3]], k = 5
输出：[0,2,0,0,0]
解释：
ID=0 的用户执行操作的分钟分别是：5 、2 和 5 。因此，该用户的用户活跃分钟数为 2（分钟 5 只计数一次）
ID=1 的用户执行操作的分钟分别是：2 和 3 。因此，该用户的用户活跃分钟数为 2
2 个用户的用户活跃分钟数都是 2 ，answer[2] 为 2 ，其余 answer[j] 的值都是 0

示例 2：

输入：logs = [[1,1],[2,2],[2,3]], k = 4
输出：[1,1,0,0]
解释：
ID=1 的用户仅在分钟 1 执行单个操作。因此，该用户的用户活跃分钟数为 1
ID=2 的用户执行操作的分钟分别是：2 和 3 。因此，该用户的用户活跃分钟数为 2
1 个用户的用户活跃分钟数是 1 ，1 个用户的用户活跃分钟数是 2 
因此，answer[1] = 1 ，answer[2] = 1 ，其余的值都是 0

提示：

• 1 <= logs.length <= 104
• 0 <= IDi <= 109
• 1 <= timei <= 105
• k 的取值范围是 [用户的最大用户活跃分钟数, 105]

2、思路1​

使用哈希表模拟

3、代码​

function findingUsersActiveMinutes(logs: number[][], k: number): number[] {
    const map = new Map<number, Set<number>>();
    for (const [id, m] of logs) {
        map.set(id, (map.get(id) ?? new Set()).add(m));
    }

    const ans = new Array(k).fill(0);
    for (const [id, set] of map) {
        if (set.size <= k) ans[set.size - 1] += 1;
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

5、执行结果​

6、思路2​

使用排序模拟，可以排序+set，也可以排序+过滤

7、代码​

排序+set

function findingUsersActiveMinutes(logs: number[][], k: number): number[] {
    logs.sort((a, b) => a[0] - b[0]);

    const ans = new Array(k).fill(0);
    for (let i = 0, set = new Set(); i < logs.length; i++) {
        set.add(logs[i][1]);
        
        if (logs[i][0] !== logs[i + 1]?.at(0)) {
            if (set.size <= k) ans[set.size - 1] += 1;
            set = new Set();
        }
    }

    return ans;
};

排序+过滤

function findingUsersActiveMinutes(logs: number[][], k: number): number[] {
    logs.sort((a, b) => a[0] === b[0] ? a[1] - b[1] : a[0] - b[0]);
    logs = logs.filter((l, i) => l[0] !== logs[i + 1]?.at(0) || l[1] !== logs[i + 1]?.at(1));

    const ans = new Array(k).fill(0);
    for (let i = 0, c = 0; i < logs.length; i++) {
        c++;
        if (logs[i][0] !== logs[i + 1]?.at(0)) {
            if (c <= k) ans[c - 1] += 1;
            c = 0;
        }
    }

    return ans;
};

8、复杂度​

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(n)$

9、执行结果​

1、题干​

给你一个数组 nums ，数组中只包含非负整数。定义 rev(x) 的值为将整数 x 各个数字位反转得到的结果。比方说 rev(123) = 321 ， rev(120) = 21 。我们称满足下面条件的下标对 (i, j) 是 好的 ：

• 0 <= i < j < nums.length
• nums[i] + rev(nums[j]) == nums[j] + rev(nums[i])

请你返回好下标对的数目。由于结果可能会很大，请将结果对 109 + 7 取余 后返回。

示例 1：

输入：nums = [42,11,1,97]
输出：2
解释：两个坐标对为：
 - (0,3)：42 + rev(97) = 42 + 79 = 121, 97 + rev(42) = 97 + 24 = 121 。
 - (1,2)：11 + rev(1) = 11 + 1 = 12, 1 + rev(11) = 1 + 11 = 12 。

示例 2：

输入：nums = [13,10,35,24,76]
输出：4

提示：

• 1 <= nums.length <= 105
• 0 <= nums[i] <= 109

2、思路​

题中的条件转换为 nums[i] - rev(nums[i]) == nums[j] - rev(nums[j])，转换后简单很多，遍历所有数字计算 nums[i] - rev(nums[i]) 并使用哈希表计数

3、代码​

function countNicePairs(nums: number[]): number {
    const M = 1e9 + 7, map = new Map();

    let ans = 0;
    for (const n of nums) {
        let cn = n, rn = 0;
        while (cn) {
            rn = 10 * rn + (cn % 10);
            cn = (cn / 10) >> 0;
        }

        const c = map.get(n - rn) || 0;
        ans = (ans + c) % M;
        map.set(n - rn, c + 1);
    }

    return ans;
};

可以使用字符串反转数字，代码更简短，但消耗的时间和内存偏多（时间：204 ms，内存：63.5 MB）。

function countNicePairs(nums: number[]): number {
    const M = 1e9 + 7, map = new Map();

    for (const n of nums) {
        const rn = +[...`${n}`].reverse().join('');
        map.set(n - rn, (map.get(n - rn) || 0) + 1);
    }

    return [...map.values()].reduce((a, c) => (a + (c * c - c) / 2) % M, 0);
};

4、复杂度​

• 时间复杂度：$O(n*logm)$，其中 $n$ 为数组长度，$m$ 为数字值
• 空间复杂度：$O(n)$

5、执行结果​

1、题干​

一个句子是由一些单词与它们之间的单个空格组成，且句子的开头和结尾没有多余空格。比方说，"Hello World" ，"HELLO" ，"hello world hello world" 都是句子。每个单词都 只 包含大写和小写英文字母。

如果两个句子 sentence1 和 sentence2 ，可以通过往其中一个句子插入一个任意的句子（可以是空句子）而得到另一个句子，那么我们称这两个句子是 相似的 。比方说，sentence1 = "Hello my name is Jane" 且 sentence2 = "Hello Jane" ，我们可以往 sentence2 中 "Hello" 和 "Jane" 之间插入 "my name is" 得到 sentence1 。

给你两个句子 sentence1 和 sentence2 ，如果 sentence1 和 sentence2 是相似的，请你返回 true ，否则返回 false 。

示例 1：

输入：sentence1 = "My name is Haley", sentence2 = "My Haley"
输出：true
解释：可以往 sentence2 中 "My" 和 "Haley" 之间插入 "name is" ，得到 sentence1 。

示例 2：

输入：sentence1 = "of", sentence2 = "A lot of words"
输出：false
解释：没法往这两个句子中的一个句子只插入一个句子就得到另一个句子。

示例 3：

输入：sentence1 = "Eating right now", sentence2 = "Eating"
输出：true
解释：可以往 sentence2 的结尾插入 "right now" 得到 sentence1 。

示例 4：

输入：sentence1 = "Luky", sentence2 = "Lucccky"
输出：false

提示：

• 1 <= sentence1.length, sentence2.length <= 100
• sentence1 和 sentence2 都只包含大小写英文字母和空格。
• sentence1 和 sentence2 中的单词都只由单个空格隔开。

2、思路1​

双指针模拟，对比首尾单词是否匹配直至指针相遇

3、代码​

function areSentencesSimilar(s1: string, s2: string): boolean {
    const words1 = s1.split(' '), words2 = s2.split(' ');
    const ml = Math.min(words1.length, words2.length);

    let i = 0, j = 0;
    while (i < ml && j < ml) {
        if (words1[i] === words2[i]) i++;
        else if (i < ml - j && words1.at(-j - 1) === words2.at(-j - 1)) j++;
        else break;
    }

    return i + j === ml;
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

5、执行结果​

6、思路2​

双端队列模拟，移除首尾相同单词直至某个队列为空。

• 没有自带的双端队列，这里使用数组代替，出队时间复杂度会更高
• 队列的实现比双指针更简单，不用考虑那么多边界问题，下次不折腾了

7、代码​

function areSentencesSimilar(s1: string, s2: string): boolean {
    const words1 = s1.split(' '), words2 = s2.split(' ');

    while (words1.length && words2.length) {
        if (words1.at(-1) === words2.at(-1)) words1.pop(), words2.pop();
        else if (words1[0] === words2[0]) words1.shift(), words2.shift();
        else break;
    }

    return !words1.length || !words2.length;
};

8、复杂度​

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

9、执行结果​

1、题干​

给你一个由正整数组成的数组 nums 。

数字序列的 最大公约数 定义为序列中所有整数的共有约数中的最大整数。

• 例如，序列 [4,6,16] 的最大公约数是 2 。

数组的一个 子序列 本质是一个序列，可以通过删除数组中的某些元素（或者不删除）得到。

• 例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。

计算并返回 nums 的所有 非空 子序列中 不同 最大公约数的 数目 。

示例 1：

输入：nums = [6,10,3]
输出：5
解释：上图显示了所有的非空子序列与各自的最大公约数。
不同的最大公约数为 6 、10 、3 、2 和 1 。

示例 2：

输入：nums = [5,15,40,5,6]
输出：7

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 2 * 105

题目太难，看了题解才写出来。

2、思路​

所有最大公约数都处于 $[1,max(nums)]$ 范围内，因此可以枚举该范围内的所有数字 i，判断该数字是否属于 nums 子序列的最大公约数。

具体判断时对 i 倍乘，若倍乘的数同时属于 nums 则求其最大公约数 g，g === i 则结果累加1。

3、代码​

function countDifferentSubsequenceGCDs(nums: number[]): number {
    let max = 0;
    for (const n of nums) max = n > max ? n : max;

    const set = new Array(max + 1);
    for (const n of nums) set[n] = 1;

    const gcd = (x: number, y: number) => y ? gcd(y, x % y) : x;

    let ans = 0;
    for (let i = 1; i <= max; i++) {
        if (set[i]) {
            ans++;
            continue;
        }

        let g = 0;
        for (let j = 2 * i; j <= max && g !== i; j += i) {
            if (set[j]) g = gcd(j, g);
        }

        if (g === i) ans++;
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n*logn)$
• 空间复杂度：$O(n)$

5、执行结果​

1、题干​

给你一个下标从 0 开始的整数数组 nums ，其长度是 2 的幂。

对 nums 执行下述算法：

1. 设 n 等于 nums 的长度，如果 n == 1 ，终止 算法过程。否则，创建 一个新的整数数组 newNums ，新数组长度为 n / 2 ，下标从 0 开始。
2. 对于满足 0 <= i < n / 2 的每个 偶数 下标 i ，将 newNums[i] 赋值 为 min(nums[2 * i], nums[2 * i + 1]) 。
3. 对于满足 0 <= i < n / 2 的每个 奇数 下标 i ，将 newNums[i] 赋值 为 max(nums[2 * i], nums[2 * i + 1]) 。
4. 用 newNums 替换 nums 。
5. 从步骤 1 开始 重复 整个过程。

执行算法后，返回 nums 中剩下的那个数字。

示例 1：

输入：nums = [1,3,5,2,4,8,2,2]
输出：1
解释：重复执行算法会得到下述数组。
第一轮：nums = [1,5,4,2]
第二轮：nums = [1,4]
第三轮：nums = [1]
1 是最后剩下的那个数字，返回 1 。

示例 2：

输入：nums = [3]
输出：3
解释：3 就是最后剩下的数字，返回 3 。

提示：

• 1 <= nums.length <= 1024
• 1 <= nums[i] <= 109
• nums.length 是 2 的幂

2、思路​

递归模拟，思路和实现比其他方式相对简单点

3、代码​

function minMaxGame(nums: number[]): number {
    if (nums.length === 1) return nums[0];

    nums = nums.slice(0, nums.length / 2).map((v, i) => {
        return (i % 2 ? Math.max : Math.min)(nums[2 * i], nums[2 * i + 1]);
    });

    return minMaxGame(nums);
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

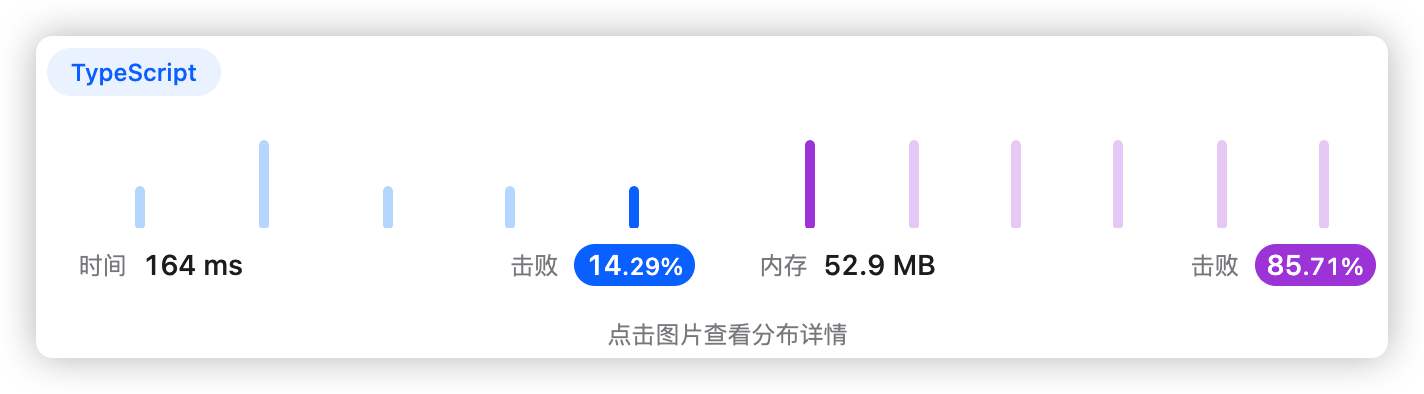
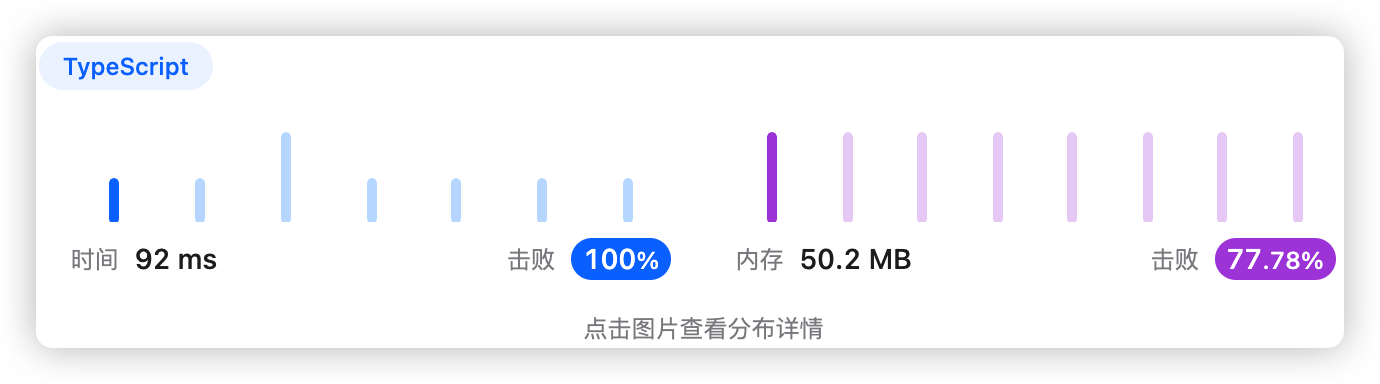
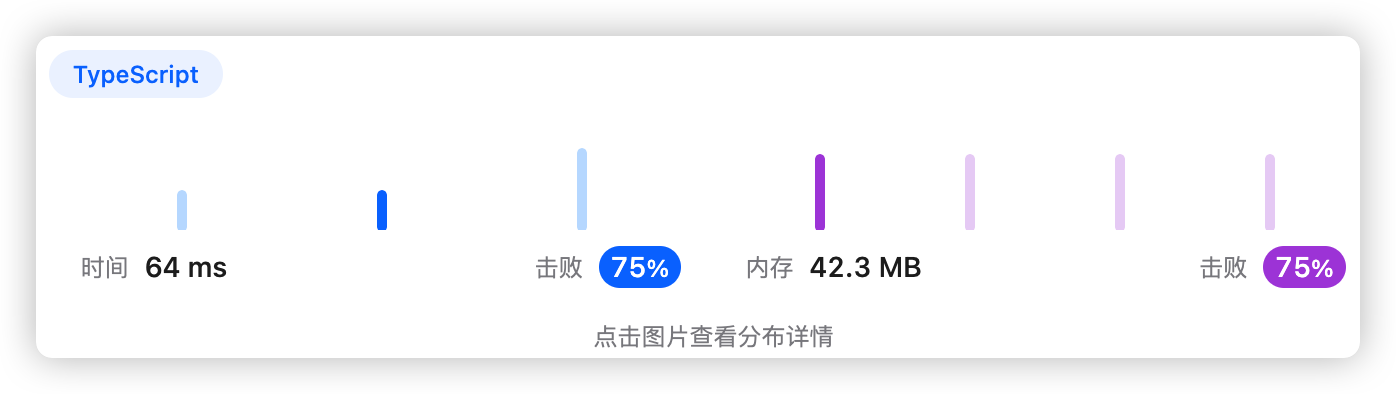
5、执行结果​