对于一个 正整数 ,如果它和除了它自身以外的所有 正因子 之和相等,我们称它为 「完美数」 。
给定一个 整数 n, 如果是完美数,返回 true;否则返回 false。
示例 1:
输入: num = 28输出: true解释: 28 = 1 + 2 + 4 + 7 + 14示例 2:
输入: num = 7输出: false
提示:
在区间 [ 1,n u m \sqrt{num} n u m n u m num n u m i,是因子则累加i + num / i(i=1时只加1),最后判断因子之和是否等于 n u m num n u m
var checkPerfectNumber = function ( num ) { let sum = 1 ; for ( let i = 2 ; i * i <= num ; i ++ ) { if ( num % i === 0 ) sum += i + num / i ; } return num === 1 ? false : sum === num ; } ; 题目比较简单,找一个正整数的所有正整数因子只需要遍历到 n \sqrt{n} n 的结论也一直记着。如果用数学归纳法,举几个例子很容易推出这个结论。
官解 这么说:如果 n {n} n n \sqrt{n} n d d d n \sqrt{n} n n d \dfrac{n}{d} d n n {n} n
但是有两个关键问题始终让人很困惑:1、为什么遍历终点是 n \sqrt{n} n ,2、因子有没有大于 n \sqrt{n} n 。实际上可以用高中数学做个推导,来解答这些困惑。过程有点繁琐,如果对过程不感兴趣可以直接看最后的结论。
假设要找正整数 n n n x x x y y y 注意:以下推导只考虑正整数范围内的情况 )
必然有x y = n xy=n x y = n y = n x y=\dfrac{n}{x} y = x n
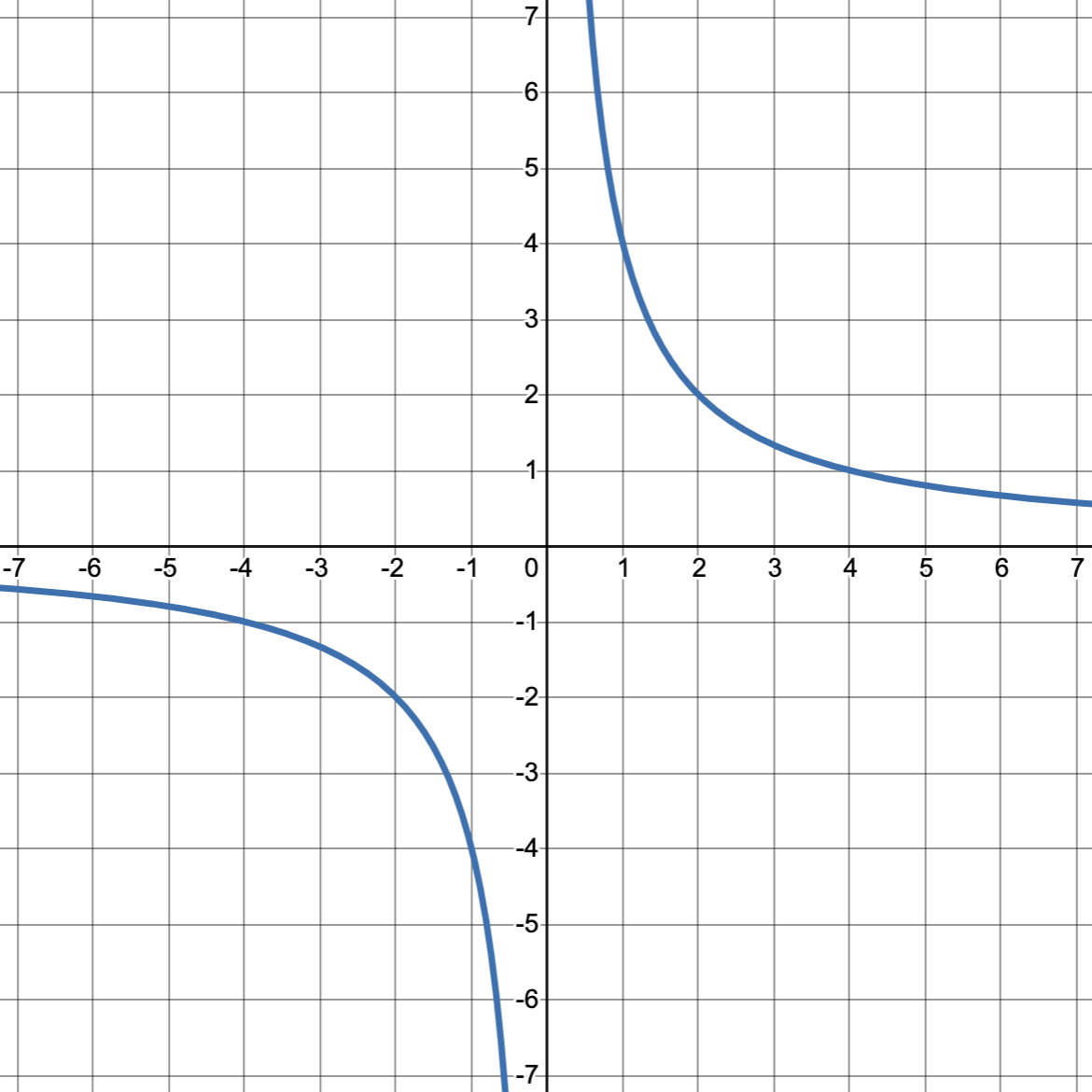
反比例函数
这个函数是不是很眼熟,没错它就是高中数学课本里的反比例函数。以 y = 4 x y=\dfrac{4}{x} y = x 4
从上图可以很容易看出,反比例函数上的任意坐标 ( x ′ , y ′ ) (x',y') ( x ′ , y ′ ) x ′ x' x ′ y ′ y' y ′ 4 4 4 n {n} n x ′ x' x ′ y ′ y' y ′
反比例函数的对称性
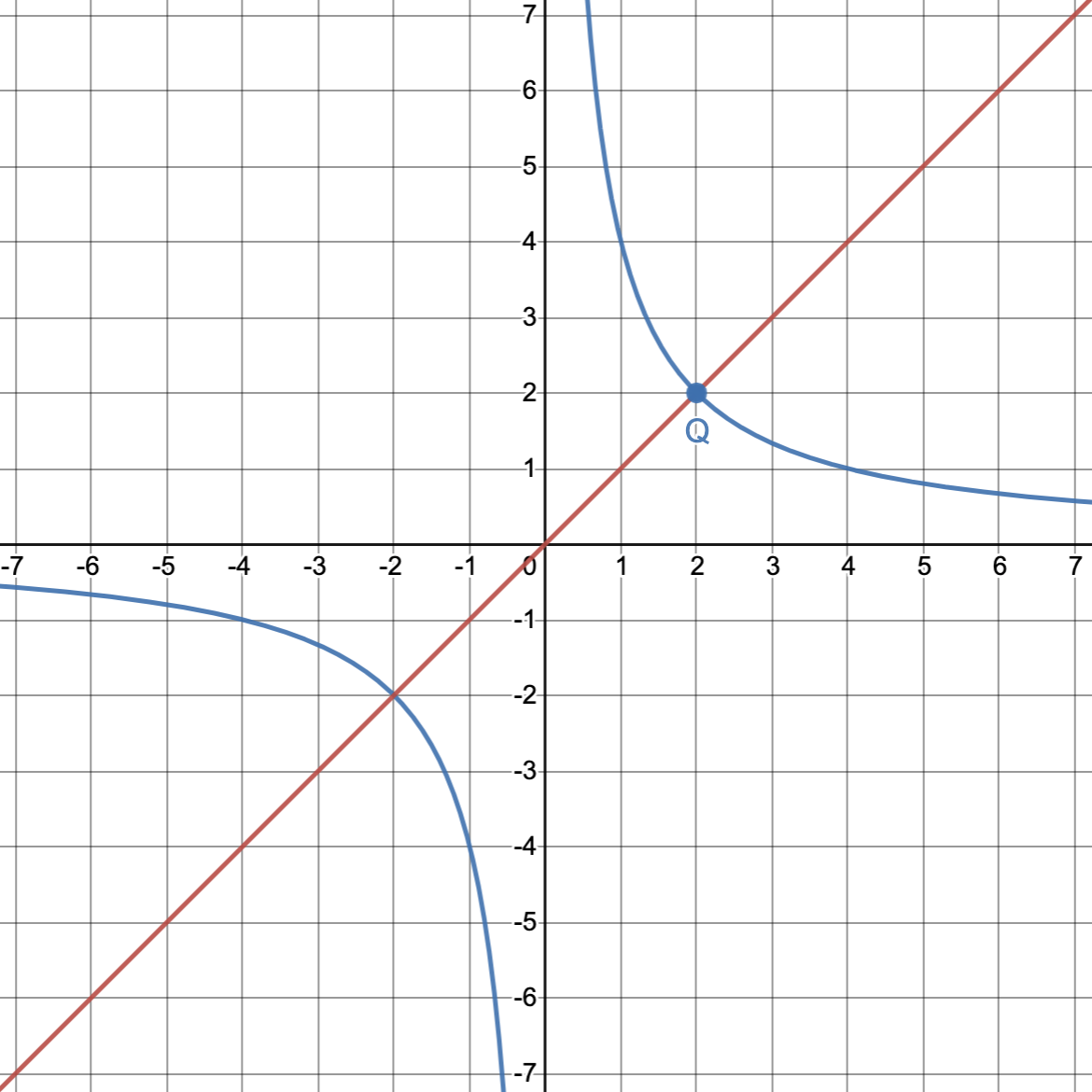
反比例函数图像是以 y = x y=x y = x y = 4 x y=\dfrac{4}{x} y = x 4
关于 y = x y=x y = x x x x y y y ( x ′ , y ′ ) (x',y') ( x ′ , y ′ ) ( y ′ , x ′ ) (y',x') ( y ′ , x ′ ) ( 4 , 1 ) (4,1) ( 4 , 1 ) y = x y=x y = x ( 1 , 4 ) (1,4) ( 1 , 4 )
由此可得 n n n ( x ′ , y ′ ) (x',y') ( x ′ , y ′ ) y = x y=x y = x
而 y = x y=x y = x y = n x y=\dfrac{n}{x} y = x n Q Q Q ( n , n ) (\sqrt{n},\sqrt{n}) ( n , n )
最后可得,假设遍历因子时取数自 x x x Q Q Q ( x ′ , y ′ ) (x',y') ( x ′ , y ′ ) x ′ < n x'<\sqrt{n} x ′ < n y ′ > n y'>\sqrt{n} y ′ > n ( y ′ , x ′ ) (y',x') ( y ′ , x ′ )
也就是说,遍历大于 n \sqrt{n} n n \sqrt{n} n n \sqrt{n} n x x x y y y 。
因此遍历到 n \sqrt{n} n n \sqrt{n} n
举个例子
n = 36 n=36 n = 36 ( 1 , 36 ) (1,36) ( 1 , 36 ) ( 2 , 18 ) (2,18) ( 2 , 18 ) ( 3 , 12 ) (3,12) ( 3 , 12 ) ( 4 , 9 ) (4,9) ( 4 , 9 ) ( 6 , 6 ) (6,6) ( 6 , 6 ) ( 9 , 4 ) (9,4) ( 9 , 4 ) ( 12 , 3 ) (12,3) ( 12 , 3 ) ( 18 , 2 ) (18,2) ( 18 , 2 ) ( 36 , 1 ) (36,1) ( 36 , 1 )
n = 81 n=81 n = 81 ( 1 , 81 ) (1,81) ( 1 , 81 ) ( 3 , 27 ) (3,27) ( 3 , 27 ) ( 9 , 9 ) (9,9) ( 9 , 9 ) ( 27 , 3 ) (27,3) ( 27 , 3 ) ( 81 , 1 ) (81,1) ( 81 , 1 )
可以发现因子对具有回文特性,这也是反比例函数对称性的体现。另外很容易看出36 36 36 81 81 81 n \sqrt{n} n
找因子之所以只需要遍历到 n \sqrt{n} n
因子之间存在反比例函数关系 y = n x y=\dfrac{n}{x} y = x n 反比例函数关于 y = x y=x y = x y = x y=x y = x 而反比例函数 y = n x y=\dfrac{n}{x} y = x n y = x y=x y = x ( n , n ) (\sqrt{n},\sqrt{n}) ( n , n ) 所以在反比例函数的图形上,任意处于交点 ( n , n ) (\sqrt{n},\sqrt{n}) ( n , n ) ( x ′ , y ′ ) (x',y') ( x ′ , y ′ ) ( y ′ , x ′ ) (y',x') ( y ′ , x ′ ) x ′ < n x'<\sqrt{n} x ′ < n y ′ > n y'>\sqrt{n} y ′ > n 所以遍历到 n \sqrt{n} n n \sqrt{n} n 也就是说,找因子只需要遍历到 n \sqrt{n} n n \sqrt{n} n n \sqrt{n} n n \sqrt{n} n x x x y y y 。 由于数轴上的数具有连续性(非离散),因此这个结论对于小数也成立。