39 篇博文 含有标签「数学」

1、题干​

复数 可以用字符串表示，遵循 "实部+虚部i" 的形式，并满足下述条件：

• 实部 是一个整数，取值范围是 [-100, 100]
• 虚部 也是一个整数，取值范围是 [-100, 100]
• i2 == -1

给你两个字符串表示的复数 num1 和 num2 ，请你遵循复数表示形式，返回表示它们乘积的字符串。

示例 1：

输入：num1 = "1+1i", num2 = "1+1i"
输出："0+2i"
解释：(1 + i) * (1 + i) = 1 + i2 + 2 * i = 2i ，你需要将它转换为 0+2i 的形式。

示例 2：

输入：num1 = "1+-1i", num2 = "1+-1i"
输出："0+-2i"
解释：(1 - i) * (1 - i) = 1 + i2 - 2 * i = -2i ，你需要将它转换为 0+-2i 的形式。 

提示：

• num1 和 num2 都是有效的复数表示。

2、解题思路​

使用正则表达式匹配出所有整数再进行计算

3、代码​

var complexNumberMultiply = function (num1, num2) {
    const [n1, n2, n3, n4] = (num1 + num2).match(/-?\d+/g).map((n) => +n);
    return `${n1 * n3 - n2 * n4}+${n1 * n4 + n2 * n3}i`;
};

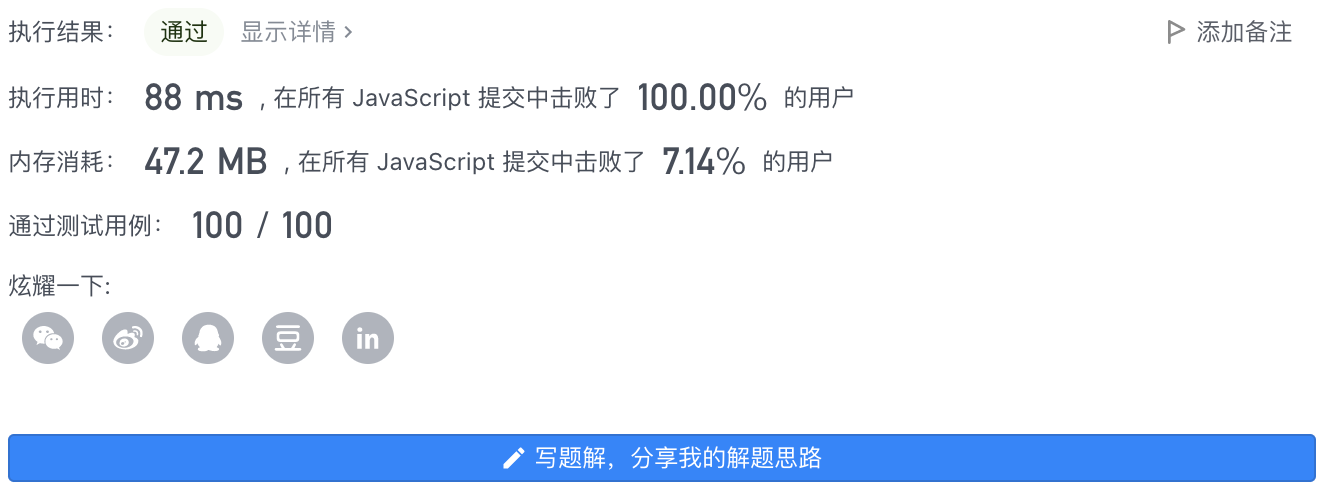
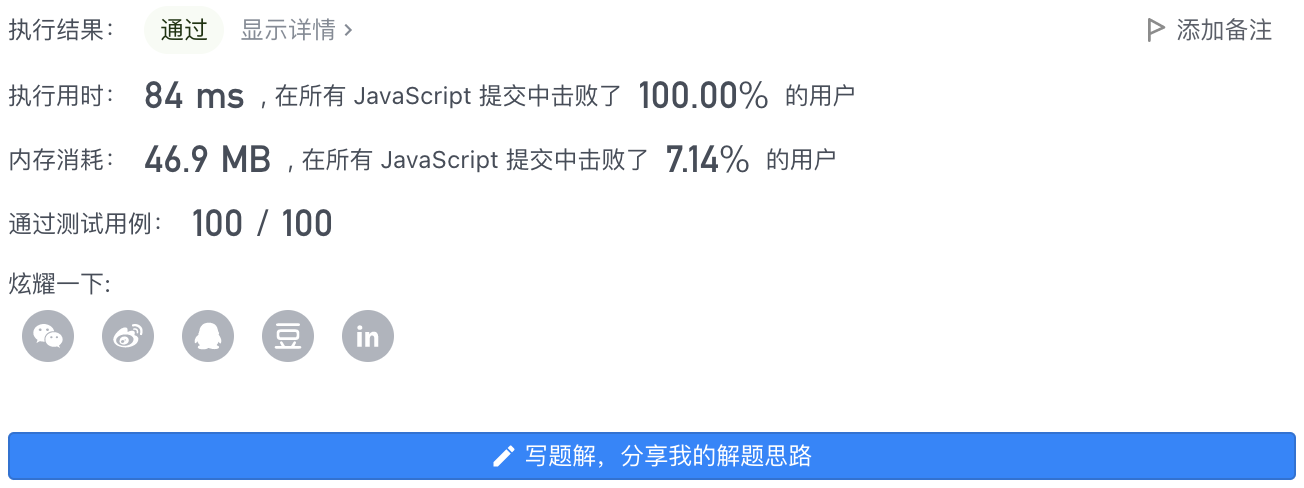
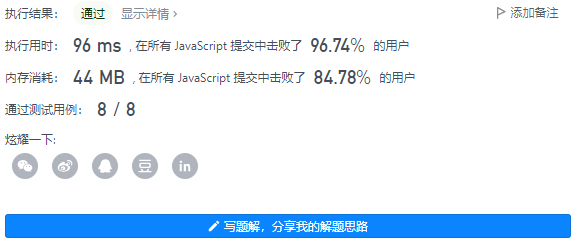
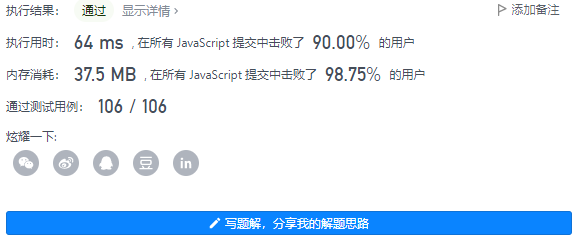
4、执行结果​

1、题干​

给你一个整数数组 nums 。如果 nums 的一个子集中，所有元素的乘积可以表示为一个或多个 互不相同的质数 的乘积，那么我们称它为 好子集 。

• 比方说，如果 nums = [1, 2, 3, 4] ：
  • [2, 3] ，[1, 2, 3] 和 [1, 3] 是 好 子集，乘积分别为 6 = 2*3 ，6 = 2*3 和 3 = 3 。
  • [1, 4] 和 [4] 不是 好 子集，因为乘积分别为 4 = 2*2 和 4 = 2*2 。

请你返回 nums 中不同的 好 子集的数目对 109 + 7 取余 的结果。

nums 中的 子集 是通过删除 nums 中一些（可能一个都不删除，也可能全部都删除）元素后剩余元素组成的数组。如果两个子集删除的下标不同，那么它们被视为不同的子集。

示例 1：

输入：nums = [1,2,3,4]
输出：6
解释：好子集为：
- [1,2]：乘积为 2 ，可以表示为质数 2 的乘积。
- [1,2,3]：乘积为 6 ，可以表示为互不相同的质数 2 和 3 的乘积。
- [1,3]：乘积为 3 ，可以表示为质数 3 的乘积。
- [2]：乘积为 2 ，可以表示为质数 2 的乘积。
- [2,3]：乘积为 6 ，可以表示为互不相同的质数 2 和 3 的乘积。
- [3]：乘积为 3 ，可以表示为质数 3 的乘积。

示例 2：

输入：nums = [4,2,3,15]
输出：5
解释：好子集为：
- [2]：乘积为 2 ，可以表示为质数 2 的乘积。
- [2,3]：乘积为 6 ，可以表示为互不相同质数 2 和 3 的乘积。
- [2,15]：乘积为 30 ，可以表示为互不相同质数 2，3 和 5 的乘积。
- [3]：乘积为 3 ，可以表示为质数 3 的乘积。
- [15]：乘积为 15 ，可以表示为互不相同质数 3 和 5 的乘积。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 30

2、解题思路​

• 状态压缩：对数组 nums 使用哈希表计数，所有的键都会集中在 $[1,30]$ 这个区间
• 从哈希表中剔除存在多个相同因子的数，比如4,8,12
• 使用 BFS 思路对符合要求的数字进行好子集组合，第一层为1个数的组合，第二层为2个数的组合，以此类推
• 组合过程中记得剔除掉存在最大公约数不为1的情况，另外注意去重
• 计算每层好子集数量并累加
  • 好子集数量等于子集各元素个数相乘
  • 若子集中存在 $1$，不是乘以 $1$ 的数量 $c1$，而应该乘以 $1$ 的组合总数 $2^{c1}-1$，由于 $c1$ 可能很大直接计算会溢出，可以使用累乘并模 $1e9+7$

这道题最大的坑在于对数字 $1$ 的特殊处理，这个解法和代码都不是最优的，抽空再优化了

3、代码​

var numberOfGoodSubsets = function (nums) {
    const MOD = 1e9 + 7;
    const nMap = nums.reduce((a, c) => a.set(c, (a.get(c) || 0) + 1), new Map());
    const bNums = [4, 9, 16, 25, 8, 27, 16];
    const gNums = [...nMap.keys()].filter(n => bNums.every((b) => n % b)).sort((a, b) => a - b);
    const gcd = (a, b) => (b ? gcd(b, a % b) : a);

    let cn1 = 1;
    for (let c1 = nMap.get(1); c1; c1--) cn1 = 2 * cn1 % MOD;

    let count = 0, queue = gNums.map((n) => [n]);
    while (queue.length) {
        const nextQueue = [];
        for (const arr of queue) {
            for (const g of gNums) {
                if (g <= arr[arr.length - 1] || arr.some((a) => gcd(a, g) > 1)) continue;
                nextQueue.push([...arr, g]);
            }

            if (arr.length === 1 && arr[0] === 1) continue;
            count += arr.reduce((a, c) => {
                const cn = c > 1 ? nMap.get(c) : cn1 - 1;
                return a * cn % MOD;
            }, 1);
            count = count % MOD;
        }
        queue = nextQueue;
    }

    return count;
};

4、执行结果​

• 执行用时: 468 ms
• 内存消耗: 63.9 MB

1、题干​

给你一个整数 n ，请你返回所有 0 到 1 之间（不包括 0 和 1）满足分母小于等于  n 的 最简 分数 。分数可以以 任意 顺序返回。

示例 1：

输入：n = 2
输出：["1/2"]
解释："1/2" 是唯一一个分母小于等于 2 的最简分数。

示例 2：

输入：n = 3
输出：["1/2","1/3","2/3"]

示例 3：

输入：n = 4
输出：["1/2","1/3","1/4","2/3","3/4"]
解释："2/4" 不是最简分数，因为它可以化简为 "1/2" 。

示例 4：

输入：n = 1
输出：[]

提示：

• 1 <= n <= 100

2、解法1-哈希表​

用哈希映射存储小数和分数字符串，其中小数作为键分数字符串作为值，最后返回哈希映射中的所有值

3、代码​

var simplifiedFractions = function (n) {
    const map = new Map();
    for (let i = 1; i < n; i++) {
        for (let j = i + 1; j <= n; j++) {
            if (!map.has(i / j)) map.set(i / j, `${i}/${j}`);
        }
    }

    return [...map.values()];
};

4、复杂度​

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

5、执行结果​

• 执行用时: 108 ms
• 内存消耗: 46.3 MB

6、解法2-求公约数​

参考求素数的方法，从 $2$ 开始遍历到 $\sqrt{n}$，看分子分母是否存在公约数

7、代码​

var simplifiedFractions = function (n) {
    function skip(min, max) {
        for (let i = 2; i * i <= max; i++) {
            if (max % i === 0 && (min % i === 0 || min % (max / i) === 0)) return true;
        }
        return false;
    }

    const res = [];
    for (let i = 1; i < n; i++) {
        for (let j = i + 1; j <= n; j++) {
            if (!skip(i, j)) res.push(i + '/' + j);
        }
    }

    return res;
};

8、复杂度​

• 时间复杂度：$O(n^2*\sqrt{n})$
• 空间复杂度：$O(n)$

9、执行结果​

• 执行用时: 88 ms
• 内存消耗: 47.2 MB

10、解法3-分母因数倍乘+哈希集合​

参考求素数的方法，从 $2$ 开始遍历到 $\sqrt{n}$，求出所有小于分母的因数及其倍乘结果并存储到哈希集合 cdSet 中，若分子存在于 cdSet 中则说明分子分母存在公约数

11、代码​

var simplifiedFractions = function (n) {
    const res = [];
    for (let i = 2; i <= n; i++) {
        const cdSet = new Set();
        for (let c = 2; c * c <= i; c++) {
            if (i % c) continue;
            for (let m = 1; m * c < i; m++) {
                cdSet.add(m * c);
                if (m * i / c < i) cdSet.add(m * i / c);
            }
        }

        for (let j = 1; j < i; j++) {
            if (!cdSet.has(j)) res.push(j + '/' + i);
        }
    }

    return res;
};

12、复杂度​

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

13、执行结果​

• 执行用时: 84 ms
• 内存消耗: 46.9 MB

1、题干​

给定一个非空的正整数数组 nums ，请判断能否将这些数字分成元素和相等的两部分。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：nums 可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：nums 不可以分为和相等的两部分

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

2、解题思路​

根据题意需要找到数组 nums 所有元素和的一半 target，可以这么做：遍历数组 nums，用哈希集合 set 记录所有元素和，若 nums 或 set 中存在 target，则返回 true。

注意 ：这个解法的关键在于必须限定 set 只能存储比 target 更小的元素和，否则大概率会超时。由于数组 nums 长度已经固定，而 set 被限制后其长度必然小于 target，因此总体时间复杂度为：$O(n*target)$，计算量级最大约为 $10^6$，超时的可能性不大。

3、代码​

var canPartition = function (nums) {
    const sum = nums.reduce((a, c) => a + c, 0);
    if (sum % 2) return false;

    const target = sum / 2, set = new Set();
    for (const n of nums) {
        if (n > target) continue;
        if (target === n || set.has(target - n)) return true;
        for (const s of [...set]) if (n + s < target) set.add(n + s);
        set.add(n);
    }

    return false;
};

4、复杂度​

• 时间复杂度：$O(n*target)$
• 空间复杂度：$O(target)$

5、执行结果​

• 执行用时: 112 ms
• 内存消耗: 47.1 MB

1、题干​

给定一个非空的正整数数组 nums ，请判断能否将这些数字分成元素和相等的两部分。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：nums 可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：nums 不可以分为和相等的两部分

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

2、解题思路​

根据题意需要找到数组 nums 所有元素和的一半 target，可以这么做：遍历数组 nums，用哈希集合 set 记录所有元素和，若 nums 或 set 中存在 target，则返回 true。

注意 ：这个解法的关键在于必须限定 set 只能存储比 target 更小的元素和，否则大概率会超时。由于数组 nums 长度已经固定，而 set 被限制后其长度必然小于 target，因此总体时间复杂度为：$O(n*target)$，计算量级最大约为 $10^6$，超时的可能性不大。

3、代码​

var canPartition = function (nums) {
    const sum = nums.reduce((a, c) => a + c, 0);
    if (sum % 2) return false;

    const target = sum / 2, set = new Set();
    for (const n of nums) {
        if (n > target) continue;
        if (target === n || set.has(target - n)) return true;
        for (const s of [...set]) if (n + s < target) set.add(n + s);
        set.add(n);
    }

    return false;
};

4、复杂度​

• 时间复杂度：$O(n*target)$
• 空间复杂度：$O(target)$

5、执行结果​

• 执行用时: 112 ms
• 内存消耗: 47.1 MB

1、题干​

给你数字 k ，请你返回和为 k 的斐波那契数字的最少数目，其中，每个斐波那契数字都可以被使用多次。

斐波那契数字定义为：

• F₁ = 1
• F₂ = 1
• F_n = F_n-1 + F_n-2 ， 其中 n > 2 。

数据保证对于给定的 k ，一定能找到可行解。

示例 1：

输入：k = 7
输出：2 
解释：斐波那契数字为：1，1，2，3，5，8，13，……
对于 k = 7 ，我们可以得到 2 + 5 = 7 。

示例 2：

输入：k = 10
输出：2 
解释：对于 k = 10 ，我们可以得到 2 + 8 = 10 。

示例 3：

输入：k = 19
输出：3 
解释：对于 k = 19 ，我们可以得到 1 + 5 + 13 = 19 。

提示：

• 1 <= k <= 10^9

2、代码​

var findMinFibonacciNumbers = function (k) {
    const nums = [1, 2];
    while (nums[nums.length - 1] < 1e9) nums.push(nums[nums.length - 1] + nums[nums.length - 2]);

    let n, count = 0;
    while (k && (n = nums.pop())) {
        if (n > k) continue;
        count += k / n >> 0;
        k = k % n;
    }
    
    return count;
};

3、执行结果​

1、题干​

你正在玩一个整数游戏。从整数 1 开始，期望得到整数 target 。

在一次行动中，你可以做下述两种操作之一：

• 递增，将当前整数的值加 1（即， x = x + 1）。
• 加倍，使当前整数的值翻倍（即，x = 2 * x）。

在整个游戏过程中，你可以使用 递增 操作 任意 次数。但是只能使用 加倍 操作 至多 maxDoubles 次。

给你两个整数 target 和 maxDoubles ，返回从 1 开始得到 target 需要的最少行动次数。

示例 1：

输入：target = 5, maxDoubles = 0
输出：4
解释：一直递增 1 直到得到 target 。

示例 2：

输入：target = 19, maxDoubles = 2
输出：7
解释：最初，x = 1 。
递增 3 次，x = 4 。
加倍 1 次，x = 8 。
递增 1 次，x = 9 。
加倍 1 次，x = 18 。
递增 1 次，x = 19 。

示例 3：

输入：target = 10, maxDoubles = 4
输出：4
解释：
最初，x = 1 。 
递增 1 次，x = 2 。 
加倍 1 次，x = 4 。 
递增 1 次，x = 5 。 
加倍 1 次，x = 10 。 

提示：

• 1 <= target <= 109
• 0 <= maxDoubles <= 100

2、解题思路​

• 使用贪心算法倒序处理，加倍变成减半，递增变成递减
• 先消耗掉所有减半次数 maxDoubles，消耗过程中如果是偶数则减半，如果是奇数则递减，每次消耗次数 count 都加1
• 剩余的操作只能是递减，需要的操作次数为剩余整数减1即 target - 1
• 最后返回 count + target - 1

3、复杂度​

• 时间复杂度：$O(logn)$
• 空间复杂度：$O(1)$

4、代码​

var minMoves = function (target, maxDoubles) {
  let count = 0;
  while (target > 1 && maxDoubles && ++count) {
    if (target % 2 === 0) maxDoubles--, (target /= 2);
    else target -= 1;
  }
  return count + target - 1;
};

5、执行结果​

• 执行用时: 64 ms
• 内存消耗: 37.8 MB

1、题干​

给你一个单链表，随机选择链表的一个节点，并返回相应的节点值。每个节点 被选中的概率一样 。

实现 Solution 类：

• Solution(ListNode head) 使用整数数组初始化对象。
• int getRandom() 从链表中随机选择一个节点并返回该节点的值。链表中所有节点被选中的概率相等。

示例：

输入
["Solution", "getRandom", "getRandom", "getRandom", "getRandom", "getRandom"]
[[[1, 2, 3]], [], [], [], [], []]
输出
[null, 1, 3, 2, 2, 3]

解释
Solution solution = new Solution([1, 2, 3]);
solution.getRandom(); // 返回 1
solution.getRandom(); // 返回 3
solution.getRandom(); // 返回 2
solution.getRandom(); // 返回 2
solution.getRandom(); // 返回 3
// getRandom() 方法应随机返回 1、2、3中的一个，每个元素被返回的概率相等。

提示：

• 链表中的节点数在范围 [1, 104] 内
• -104 <= Node.val <= 104
• 至多调用 getRandom 方法 104 次

进阶：

• 如果链表非常大且长度未知，该怎么处理？
• 你能否在不使用额外空间的情况下解决此问题？

2、解题思路​

数组存储所有节点值，getRandom 时使用随机数 API 生成随机序号并返回数组内相应的值。

3、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

4、代码​

var Solution = function (head) {
    this.list = [];
    while (head) {
        this.list.push(head.val);
        head = head.next;
    }
};

Solution.prototype.getRandom = function () {
    return this.list[Math.floor(Math.random() * this.list.length)];
};

5、执行结果​

1、题干​

Hercy 想要为购买第一辆车存钱。他 每天 都往力扣银行里存钱。

最开始，他在周一的时候存入 1 块钱。从周二到周日，他每天都比前一天多存入 1 块钱。在接下来每一个周一，他都会比 前一个周一 多存入 1 块钱。

给你 n ，请你返回在第 n 天结束的时候他在力扣银行总共存了多少块钱。

示例 1：

输入：n = 4
输出：10
解释：第 4 天后，总额为 1 + 2 + 3 + 4 = 10 。

示例 2：

输入：n = 10
输出：37
解释：第 10 天后，总额为 (1 + 2 + 3 + 4 + 5 + 6 + 7) + (2 + 3 + 4) = 37 。注意到第二个星期一，Hercy 存入 2 块钱。

示例 3：

输入：n = 20
输出：96
解释：第 20 天后，总额为 (1 + 2 + 3 + 4 + 5 + 6 + 7) + (2 + 3 + 4 + 5 + 6 + 7 + 8) + (3 + 4 + 5 + 6 + 7 + 8) = 96 。

提示：

• 1 <= n <= 1000

2、解题思路​

• 计算存款总额可以分为两部分，前半部分按整周计算，后半部分不足一周按天计算，两部分都是等差数列，分别求和后再相加即可
• 先计算周数 $w = n / 7 >> 0$ 和不足一周的天数 $d = n \% 7$
• 前半部分按周计算，其数列为：$28 + (28 + 7) + ... + (28 + (w-1)*7)$ ，共 $w$ 项，和为 $28 * w + 7 * w * (w - 1) / 2$
• 后半部分按天计算，其数列为：$(1 + w) + (2 + w) + ... + (d + w)$ ，共 $d$ 项，和为$d * w + d * (d + 1) / 2$

3、复杂度​

• 时间复杂度：$O(1)$
• 空间复杂度：$O(1)$

4、代码​

var totalMoney = function (n) {
    const w = n / 7 >> 0, d = n % 7;
    return 28 * w + 7 * w * (w - 1) / 2 + d * w + d * (d + 1) / 2;
};

5、执行结果​

1、题干​

• 每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）
• 第一个整数是 0
• 一个整数在序列中出现 不超过一次
• 每对 相邻 整数的二进制表示 恰好一位不同 ，且
• 第一个 和 最后一个 整数的二进制表示 恰好一位不同

给你一个整数 n ，返回任一有效的 n 位格雷码序列 。

示例 1：

输入：n = 2
输出：[0,1,3,2]
解释：
[0,1,3,2] 的二进制表示是 [00,01,11,10] 。
- 00 和 01 有一位不同
- 01 和 11 有一位不同
- 11 和 10 有一位不同
- 10 和 00 有一位不同
[0,2,3,1] 也是一个有效的格雷码序列，其二进制表示是 [00,10,11,01] 。
- 00 和 10 有一位不同
- 10 和 11 有一位不同
- 11 和 01 有一位不同
- 01 和 00 有一位不同

示例 2：

输入：n = 1
输出：[0,1]

提示：

• 1 <= n <= 16

格雷编码的生成方式有3种，直接计算、镜像对称构造、交替构造；可惜我一个都没推出来，这里做个简单记录。

2、直接计算​

直接计算的公式是：$G(n) = n \oplus \dfrac{n}{2}$。其中 $G(n)$ 表示第 $n$ 个格雷码。

该解法对应官解2

3、代码​

var grayCode = function(n) {
    const ret = [];
    for (let i = 0; i < 1 << n; i++) {
        ret.push((i >> 1) ^ i);
    }
    return ret;
};

4、镜像对称构造​

• 将前2k个格雷码去除首位二进制数并分成两半后具有镜像对称性。（如下图3位格雷码）
• n位格雷码是将n-1位格雷码作为前半部分，将n-1位格雷码倒序遍历并在其二进制数之前添1作为后半部分。（如下图3位格雷码与2位格雷码关系）

该解法对应官解1

5、代码​

var grayCode = function (n) {
    const arr = [0, 1];
    for (let i = 2; i <= n; i++) {
        for (let j = arr.length - 1; j > -1; j--) {
            arr.push(arr[j] | (1 << (i - 1)));
        }
    }
    return arr;
};

6、交替构造​

以3位格雷码为例：

• 从 n = 0 开始，按以下2步反复操作，即可得到所有格雷码
• n 为偶数：翻转最低位得到下一个格雷码，如 000 变成 001
• n 为奇数：把最右边的 1 左边的位翻转得到下一个格雷码，如 001 变成 011

实现略复杂，暂无代码，建议优先使用前2种方法生成