28 篇博文 含有标签「排序」

1、题干​

如果可以使用以下操作从一个字符串得到另一个字符串，则认为两个字符串 接近 ：

• 操作 1：交换任意两个 现有 字符。
  • 例如，abcde -> aecdb
• 操作 2：将一个 现有 字符的每次出现转换为另一个 现有 字符，并对另一个字符执行相同的操作。
  • 例如，aacabb -> bbcbaa（所有 a 转化为 b ，而所有的 b 转换为 a ）

你可以根据需要对任意一个字符串多次使用这两种操作。

给你两个字符串，word1 和 word2 。如果 word1 和 word2 接近 ，就返回 true ；否则，返回 false 。

示例 1：

输入：word1 = "abc", word2 = "bca"
输出：true
解释：2 次操作从 word1 获得 word2 。
执行操作 1："abc" -> "acb"
执行操作 1："acb" -> "bca"

示例 2：

输入：word1 = "a", word2 = "aa"
输出：false
解释：不管执行多少次操作，都无法从 word1 得到 word2 ，反之亦然。

示例 3：

输入：word1 = "cabbba", word2 = "abbccc"
输出：true
解释：3 次操作从 word1 获得 word2 。
执行操作 1："cabbba" -> "caabbb"
执行操作 2："caabbb" -> "baaccc"
执行操作 2："baaccc" -> "abbccc"

示例 4：

输入：word1 = "cabbba", word2 = "aabbss"
输出：false
解释：不管执行多少次操作，都无法从 word1 得到 word2 ，反之亦然。

提示：

• 1 <= word1.length, word2.length <= 105
• word1 和 word2 仅包含小写英文字母

2、思路​

需要校验两个关键点：

• 两个字符串包含的字母相同
• 两个字符串分别按字母计数，计数结果排序后相同

3、代码​

function closeStrings(word1: string, word2: string): boolean {
    if (word1.length !== word2.length) return false;

    const K = 26, AC = 'a'.charCodeAt(0);
    const c1 = new Array(K).fill(0), c2 = new Array(K).fill(0);

    for (let i = 0; i < word1.length; i++) {
        c1[word1.charCodeAt(i) - AC] += 1;
        c2[word2.charCodeAt(i) - AC] += 1;
    }

    return c1.every((c, i) => +!c === +!c2[i]) && c1.sort().toString() === c2.sort().toString();
};

1、题干​

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

提示：

• nums1.length == m + n
• nums2.length == n
• 0 <= m, n <= 200
• 1 <= m + n <= 200
• -109 <= nums1[i], nums2[j] <= 109

进阶：你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗？

2、思路​

两种思路：双指针，合并后排序（无脑暴力）

3、代码​

• 双指针

function merge(nums1: number[], m: number, nums2: number[], n: number): void {
    const arr1 = nums1.slice(0, m), arr2 = nums2;

    for (let k = 0, i = 0, j = 0; k < m + n; k++) {
        nums1[k] = j >= n || arr1[i] <= arr2[j] ? arr1[i++] : arr2[j++];
    }
};

官解的逆向双指针更优秀，空间复杂度为 $O(1)$，即不需要另外开辟数组辅助，而是优先将结果填充到 nums1 尾部区域

• 合并排序

var merge = function (nums1, m, nums2, n) {
    nums1.splice(m, n, ...nums2);
    return nums1.sort((a, b) => a - b);
};

1、题干​

给你两个正整数数组 spells 和 potions ，长度分别为 n 和 m ，其中 spells[i] 表示第 i 个咒语的能量强度，potions[j] 表示第 j 瓶药水的能量强度。

同时给你一个整数 success 。一个咒语和药水的能量强度 相乘 如果 大于等于 success ，那么它们视为一对 成功 的组合。

请你返回一个长度为 n 的整数数组 pairs，其中 pairs[i] 是能跟第 i 个咒语成功组合的 药水 数目。

示例 1：

输入：spells = [5,1,3], potions = [1,2,3,4,5], success = 7
输出：[4,0,3]
解释：
- 第 0 个咒语：5 * [1,2,3,4,5] = [5,10,15,20,25] 。总共 4 个成功组合。
- 第 1 个咒语：1 * [1,2,3,4,5] = [1,2,3,4,5] 。总共 0 个成功组合。
- 第 2 个咒语：3 * [1,2,3,4,5] = [3,6,9,12,15] 。总共 3 个成功组合。
所以返回 [4,0,3] 。

示例 2：

输入：spells = [3,1,2], potions = [8,5,8], success = 16
输出：[2,0,2]
解释：
- 第 0 个咒语：3 * [8,5,8] = [24,15,24] 。总共 2 个成功组合。
- 第 1 个咒语：1 * [8,5,8] = [8,5,8] 。总共 0 个成功组合。
- 第 2 个咒语：2 * [8,5,8] = [16,10,16] 。总共 2 个成功组合。
所以返回 [2,0,2] 。

提示：

• n == spells.length
• m == potions.length
• 1 <= n, m <= 105
• 1 <= spells[i], potions[i] <= 105
• 1 <= success <= 1010

2、思路​

对 potions 排序，遍历 spells 并使用二分查找统计 potions 中不小于 success / spells[i] 的元素数量，复杂度 $O(n\log{n})$

3、代码​

function successfulPairs(spells: number[], potions: number[], success: number): number[] {
    potions.sort((a, b) => a - b);
    const pairs = new Array(spells.length).fill(0);

    for (let i = 0; i < spells.length; i++) {
        const s = success / spells[i];
        pairs[i] = search(potions, s);
    }

    return pairs;
};

function search(arr: number[], k: number) {
    let m = 0, l = 0, r = arr.length - 1;
    while (l <= r) {
        m = (l + r) >> 1;

        if (arr[m] >= k) {
            r = m - 1;
        } else {
            l = m + 1;
        }
    }

    return arr.length - l;
}

1、题干​

如果一个数列由至少两个元素组成，且每两个连续元素之间的差值都相同，那么这个序列就是 等差数列 。更正式地，数列 s 是等差数列，只需要满足：对于每个有效的 i ， s[i+1] - s[i] == s[1] - s[0] 都成立。

例如，下面这些都是 等差数列 ：

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

下面的数列 不是等差数列 ：

1, 1, 2, 5, 7

给你一个由 n 个整数组成的数组 nums，和两个由 m 个整数组成的数组 l 和 r，后两个数组表示 m 组范围查询，其中第 i 个查询对应范围 [l[i], r[i]] 。所有数组的下标都是 从 0 开始 的。

返回 boolean 元素构成的答案列表 answer 。如果子数组 nums[l[i]], nums[l[i]+1], ... , nums[r[i]] 可以 重新排列 形成 等差数列 ，answer[i] 的值就是 true；否则answer[i] 的值就是 false 。

示例 1：

输入：nums = [4,6,5,9,3,7], l = [0,0,2], r = [2,3,5]
输出：[true,false,true]
解释：
第 0 个查询，对应子数组 [4,6,5] 。可以重新排列为等差数列 [6,5,4] 。
第 1 个查询，对应子数组 [4,6,5,9] 。无法重新排列形成等差数列。
第 2 个查询，对应子数组 [5,9,3,7] 。可以重新排列为等差数列 [3,5,7,9] 。

示例 2：

输入：nums = [-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10], l = [0,1,6,4,8,7], r = [4,4,9,7,9,10]
输出：[false,true,false,false,true,true]

提示：

• n == nums.length
• m == l.length
• m == r.length
• 2 <= n <= 500
• 1 <= m <= 500
• 0 <= l[i] < r[i] < n
• -105 <= nums[i] <= 105

2、思路1​

模拟+计数排序

3、代码​

function checkArithmeticSubarrays(nums: number[], l: number[], r: number[]): boolean[] {
    const ans = new Array(l.length).fill(true);

    for (let i = 0; i < l.length; i++) {
        const len = r[i] - l[i] + 1;
        if (len < 3) continue;

        let min = 1e5, max = -1e5;
        for (let j = l[i]; j <= r[i]; j++) {
            min = Math.min(nums[j], min);
            max = Math.max(nums[j], max);
        }

        if (min === max) continue;

        const d = (max - min) / (len - 1);
        const buckt = new Array(len).fill(0);

        for (let j = l[i]; j <= r[i]; j++) {
            const m = (nums[j] - min) % d;
            const bi = (nums[j] - min) / d;
            if (m || buckt[bi]) {
                ans[i] = false;
                break;
            }
            buckt[bi] = 1;
        }
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

5、执行结果​

6、思路2​

模拟+排序API

7、代码​

function checkArithmeticSubarrays(nums: number[], l: number[], r: number[]): boolean[] {
    const ans = l.map(() => true);

    for (let i = 0; i < l.length; i++) {
        if (r[i] - l[i] < 2) continue;
        const arr = nums.slice(l[i], r[i] + 1).sort((a, b) => a - b);

        const d = arr[1] - arr[0];
        for (let j = 2; j < arr.length; j++) {
            if (arr[j] - arr[j - 1] !== d) {
                ans[i] = false;
                break;
            }
        }
    }

    return ans;
};

8、复杂度​

• 时间复杂度：$O(n^2 \log{n})$
• 空间复杂度：$O(n)$

9、执行结果​

1、题干​

给你一个长度为 n 的整数数组 nums ，和一个长度为 m 的整数数组 queries 。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是 nums 中 元素之和小于等于 queries[i] 的 子序列 的 最大 长度  。

子序列 是由一个数组删除某些元素（也可以不删除）但不改变剩余元素顺序得到的一个数组。

示例 1：

输入：nums = [4,5,2,1], queries = [3,10,21]
输出：[2,3,4]
解释：queries 对应的 answer 如下：
- 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ，所以 answer[0] = 2 。
- 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ，所以 answer[1] = 3 。
- 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ，所以 answer[2] = 4 。

示例 2：

输入：nums = [2,3,4,5], queries = [1]
输出：[0]
解释：空子序列是唯一一个满足元素和小于或等于 1 的子序列，所以 answer[0] = 0 。

提示：

• n == nums.length
• m == queries.length
• 1 <= n, m <= 1000
• 1 <= nums[i], queries[i] <= 106

2、思路1-暴力​

• 对 nums 升序排序，求前缀和
• 暴力查找不大于 queries[i] 的前缀和数量

3、代码​

function answerQueries(nums: number[], queries: number[]): number[] {
    nums.sort((a, b) => a - b);
    for (let i = 1; i < nums.length; i++) nums[i] += nums[i - 1];

    let ans = queries.map(Number);
    for (let i = 0; i < queries.length; i++) {
        if (nums.at(-1) <= queries[i]) ans[i] = nums.length;
        else ans[i] = nums.findIndex((s) => s > queries[i]);
    }

    return ans;
};

4、复杂度​

• 时间复杂度： $O(n^2)$
• 空间复杂度： $O(\log{n})$

5、执行结果​

6、思路2-排序优化​

在思路1的基础上进行优化，如果 queries 是升序数组，那么查找子序列就不用每次都从头到尾遍历前缀和数组，可以从上一个找到的前缀和下标开始往后查找，查找过程复杂度从 $O(n^2)$ 降到 $O(n)$

7、代码​

function answerQueries(nums: number[], queries: number[]): number[] {
    nums.sort((a, b) => a - b);
    for (let i = 1; i < nums.length; i++) nums[i] += nums[i - 1];

    const qs = queries.map((n, i) => [n, i]).sort((a, b) => a[0] - b[0]);

    let ans = queries.map(Number);
    for (let i = 0, j = 0; i < qs.length; i++) {
        if (nums.at(-1) <= qs[i][0]) {
            ans[qs[i][1]] = nums.length;
            continue;
        }

        while (nums[j] <= qs[i][0]) j++;
        ans[qs[i][1]] = j;
    }

    return ans;
};

8、复杂度​

• 时间复杂度： $O(n \log{n})$
• 空间复杂度： $O(n)$

9、执行结果​

1、题干​

给你两个二维整数数组 items1 和 items2 ，表示两个物品集合。每个数组 items 有以下特质：

• items[i] = [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ，weighti 表示第 i 件物品的 重量 。
• items 中每件物品的价值都是 唯一的 。

请你返回一个二维数组 ret，其中 ret[i] = [valuei, weighti]， weighti 是所有价值为 valuei 物品的 重量之和 。

注意：ret 应该按价值 升序 排序后返回。

示例 1：

输入：items1 = [[1,1],[4,5],[3,8]], items2 = [[3,1],[1,5]]
输出：[[1,6],[3,9],[4,5]]
解释：
value = 1 的物品在 items1 中 weight = 1 ，在 items2 中 weight = 5 ，总重量为 1 + 5 = 6 。
value = 3 的物品再 items1 中 weight = 8 ，在 items2 中 weight = 1 ，总重量为 8 + 1 = 9 。
value = 4 的物品在 items1 中 weight = 5 ，总重量为 5 。
所以，我们返回 [[1,6],[3,9],[4,5]] 。

示例 2：

输入：items1 = [[1,1],[3,2],[2,3]], items2 = [[2,1],[3,2],[1,3]]
输出：[[1,4],[2,4],[3,4]]
解释：
value = 1 的物品在 items1 中 weight = 1 ，在 items2 中 weight = 3 ，总重量为 1 + 3 = 4 。
value = 2 的物品在 items1 中 weight = 3 ，在 items2 中 weight = 1 ，总重量为 3 + 1 = 4 。
value = 3 的物品在 items1 中 weight = 2 ，在 items2 中 weight = 2 ，总重量为 2 + 2 = 4 。
所以，我们返回 [[1,4],[2,4],[3,4]] 。

示例 3：

输入：items1 = [[1,3],[2,2]], items2 = [[7,1],[2,2],[1,4]]
输出：[[1,7],[2,4],[7,1]]
解释：
value = 1 的物品在 items1 中 weight = 3 ，在 items2 中 weight = 4 ，总重量为 3 + 4 = 7 。
value = 2 的物品在 items1 中 weight = 2 ，在 items2 中 weight = 2 ，总重量为 2 + 2 = 4 。
value = 7 的物品在 items2 中 weight = 1 ，总重量为 1 。
所以，我们返回 [[1,7],[2,4],[7,1]] 。

提示：

• 1 <= items1.length, items2.length <= 1000
• items1[i].length == items2[i].length == 2
• 1 <= valuei, weighti <= 1000
• items1 中每个 valuei 都是 唯一的 。
• items2 中每个 valuei 都是 唯一的 。

2、思路1-整合+排序​

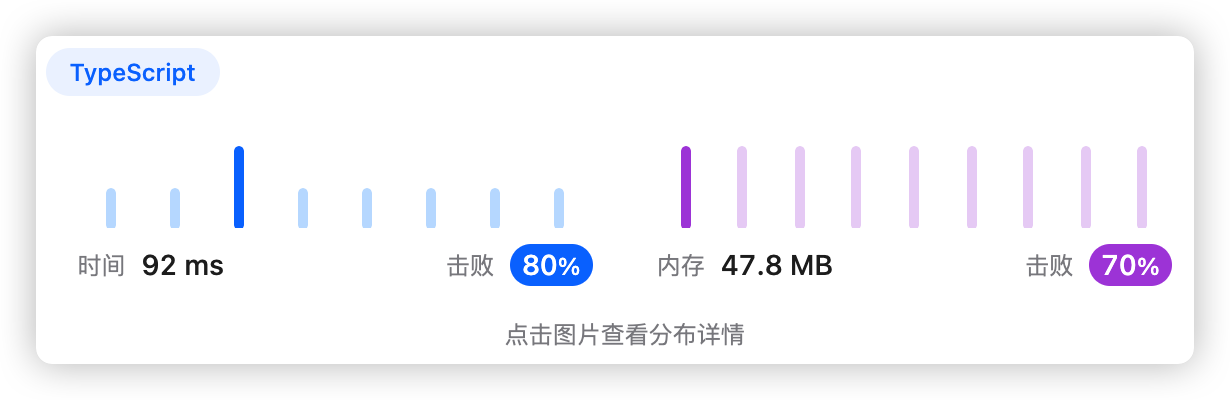
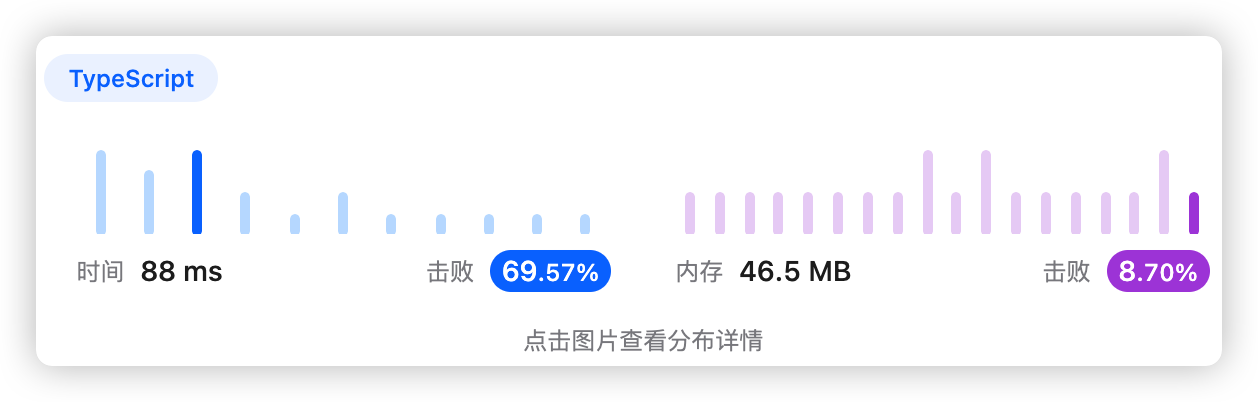
整合两个数组再统一升序排序，接着遍历所有物品得到结果

3、代码​

function mergeSimilarItems(items1: number[][], items2: number[][]): number[][] {
    items1.push(...items2);
    items1.sort((a, b) => a[0] - b[0]);

    const ans = [];
    for (let i = 0; i < items1.length; i++) {
        if (items1[i][0] === items1[i + 1]?.at(0)) items1[i + 1][1] += items1[i][1];
        else ans.push(items1[i]);
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n \log n)$
• 空间复杂度：$O(n)$

5、执行结果​

6、思路2-桶排序​

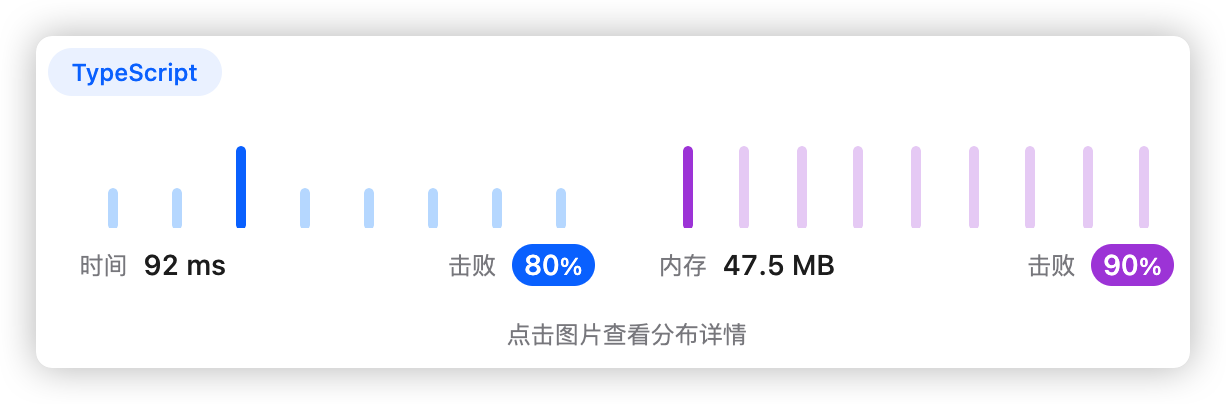
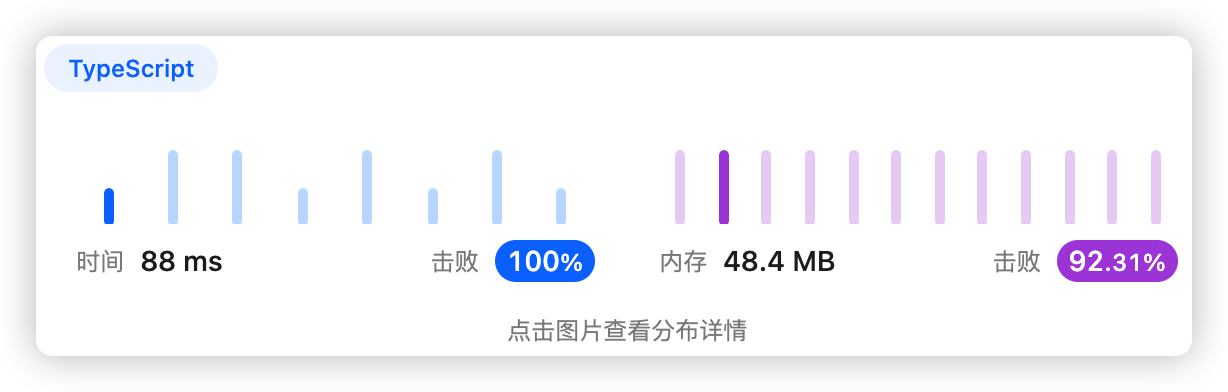
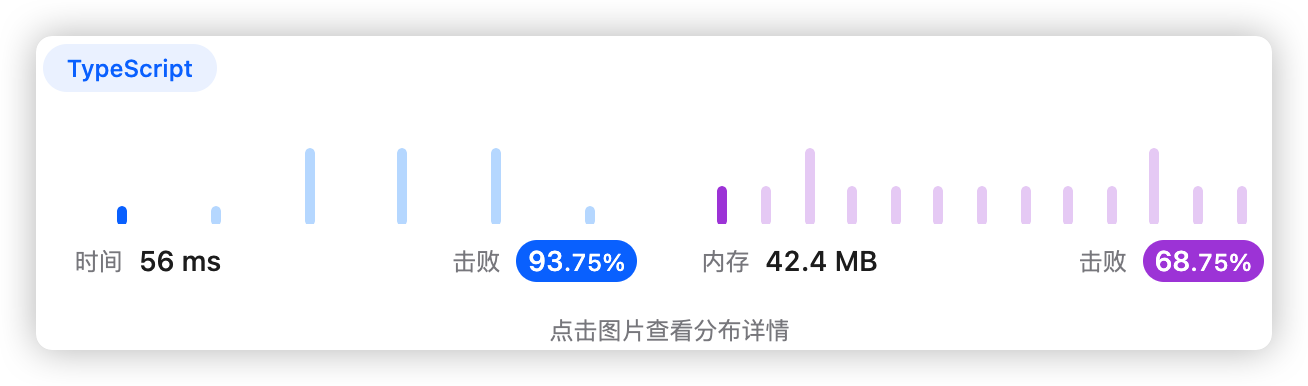
以价值作为桶序号，累加物品重量，最后返回重量大于0的桶序号及其重量

桶内不需要再排序，而是累加数值，跟常见的桶排序有点不同

7、代码​

function mergeSimilarItems(items1: number[][], items2: number[][]): number[][] {
    const bucket = new Array(1001).fill(0);
    for (let i = 0; i < items1.length || i < items2.length; i++) {
        if (items1[i]) bucket[items1[i][0]] += items1[i][1];
        if (items2[i]) bucket[items2[i][0]] += items2[i][1];
    }

    return bucket.map((w, i) => [i, w]).filter(b => b[1]);
};

8、复杂度​

• 时间复杂度：$O(max(C,n))$
• 空间复杂度：$O(C)$

9、执行结果​

10、思路3-哈希+排序​

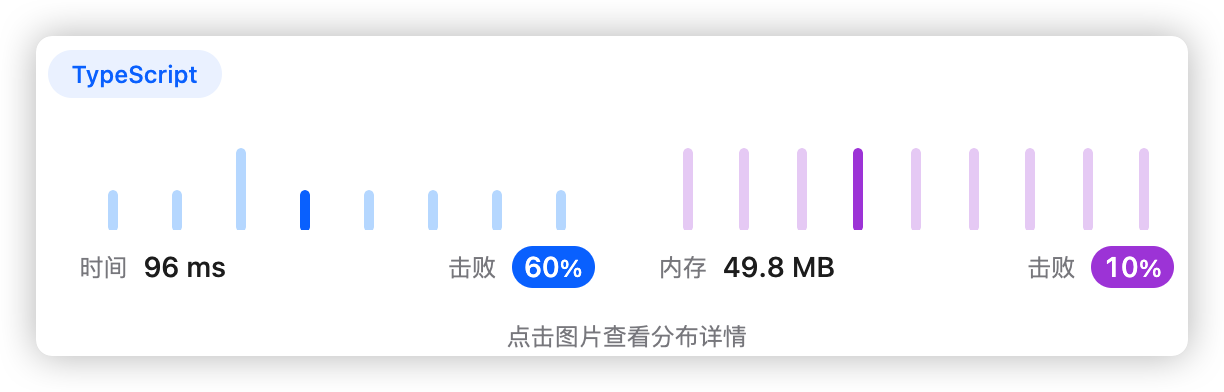
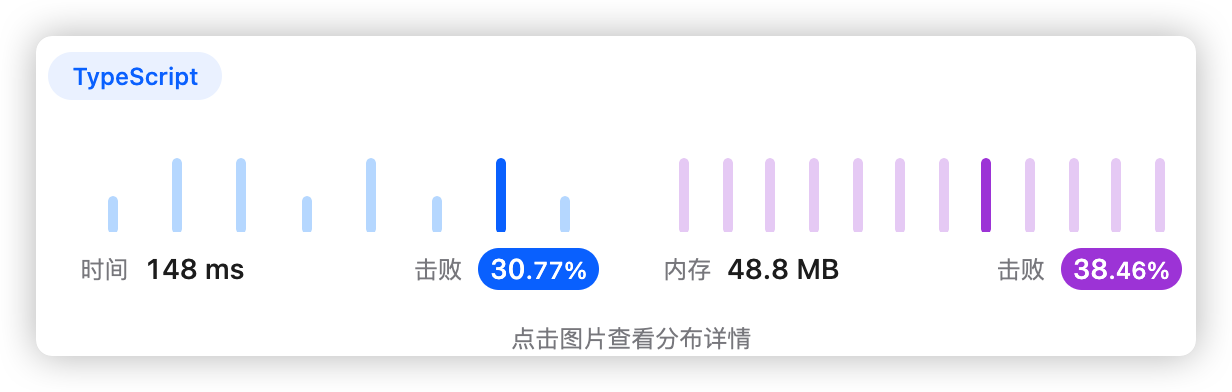
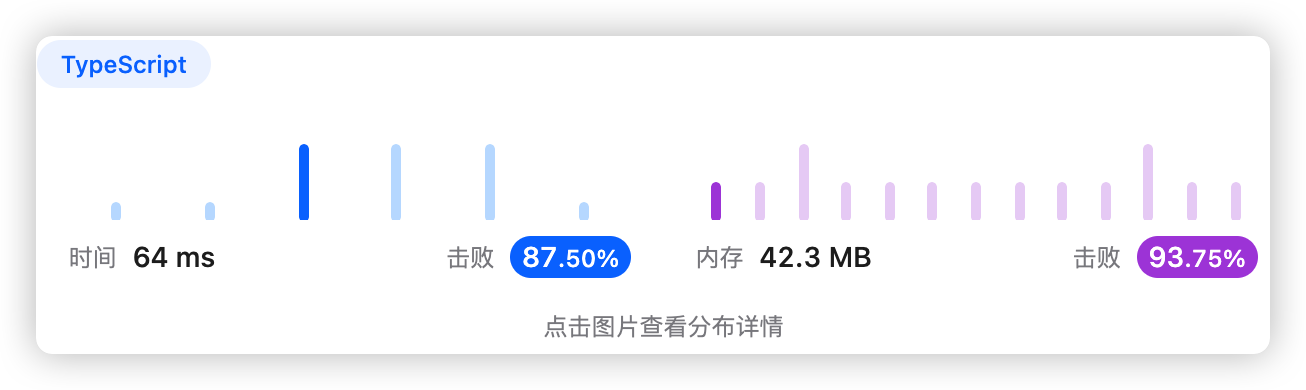
以价值作为哈希表的键，累加物品重量，最后返回按键升序排序的键值对

11、代码​

function mergeSimilarItems(items1: number[][], items2: number[][]): number[][] {
    const map = new Map();
    for (let i = 0; i < items1.length || i < items2.length; i++) {
        if (items1[i]) map.set(items1[i][0], (map.get(items1[i][0]) || 0) + items1[i][1]);
        if (items2[i]) map.set(items2[i][0], (map.get(items2[i][0]) || 0) + items2[i][1]);
    }

    return [...map].sort((a, b) => a[0] - b[0]);
};

12、复杂度​

• 时间复杂度：$O(n \log n)$
• 空间复杂度：$O(n)$

13、执行结果​

14、思路4-双指针+排序​

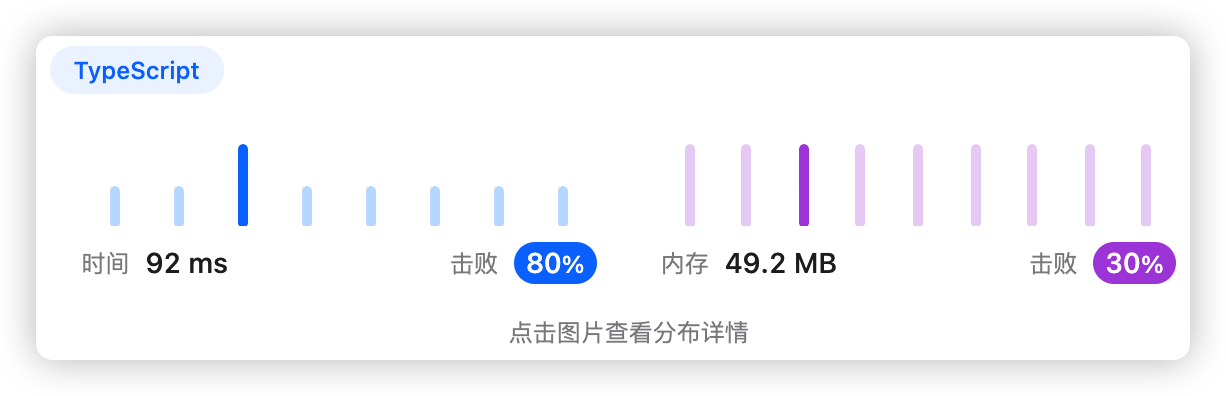
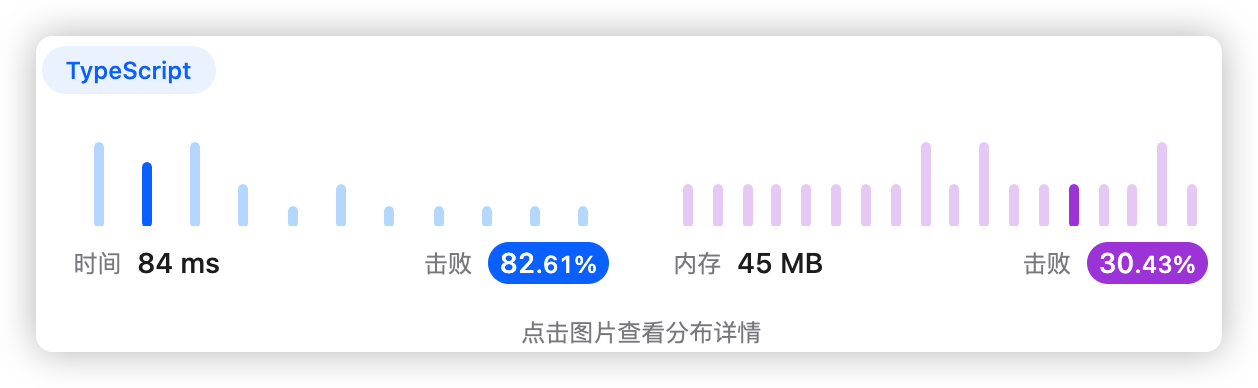
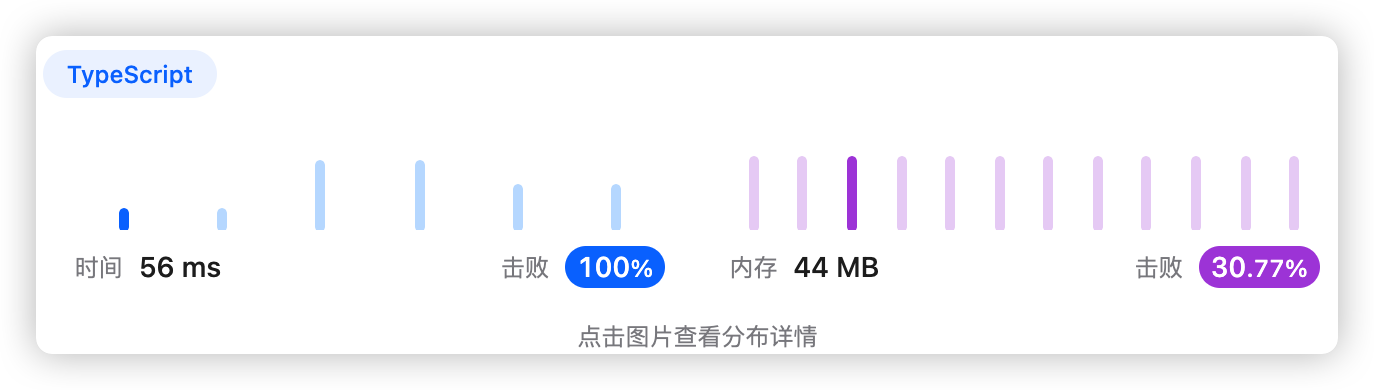
先对两个数组分别排序，再使用双指针按价值从小到大遍历所有物品

15、代码​

function mergeSimilarItems(items1: number[][], items2: number[][]): number[][] {
    items1.sort((a, b) => a[0] - b[0]);
    items2.sort((a, b) => a[0] - b[0]);

    const ans = [];
    for (let i = 0, j = 0; i < items1.length || j < items2.length;) {
        while (i < items1.length && (!items2[j] || items1[i][0] < items2[j][0])) {
            ans.push(items1[i]);
            i++;
        }

        while (j < items2.length && (!items1[i] || items1[i][0] > items2[j][0])) {
            ans.push(items2[j]);
            j++;
        }

        if (i < items1.length && j < items2.length && items1[i][0] === items2[j][0]) {
            items1[i][1] += items2[j][1];
            ans.push(items1[i]);
            i++, j++;
        }
    }

    return ans;
};

16、复杂度​

• 时间复杂度：$O(n \log n)$
• 空间复杂度：$O(\log n)$

17、执行结果​

1、题干​

给你一个非负整数数组 nums 。在一步操作中，你必须：

• 选出一个正整数 x ，x 需要小于或等于 nums 中 最小 的 非零 元素。
• nums 中的每个正整数都减去 x。

返回使 nums 中所有元素都等于 0 需要的 最少 操作数。

示例 1：

输入：nums = [1,5,0,3,5]
输出：3
解释：
第一步操作：选出 x = 1 ，之后 nums = [0,4,0,2,4] 。
第二步操作：选出 x = 2 ，之后 nums = [0,2,0,0,2] 。
第三步操作：选出 x = 2 ，之后 nums = [0,0,0,0,0] 。

示例 2：

输入：nums = [0]
输出：0
解释：nums 中的每个元素都已经是 0 ，所以不需要执行任何操作。

提示：

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 100

2、思路1​

根据题目描述，每一步都消除了所有最小的正整数，因此最少步数就是数组 nums 去重后正整数的个数。

第一个思路是：排序后统计去重正整数个数

3、代码​

function minimumOperations(nums: number[]): number {
    nums.sort((a, b) => a - b);

    let step = 0;
    for (let i = 0; i < nums.length; i++) {
        if (nums[i] && nums[i] !== nums[i - 1]) step++;
    }

    return step;
};

4、复杂度​

• 时间复杂度：$O(n \log n)$
• 空间复杂度：$O(\log n)$

5、执行结果​

6、思路2​

哈希去重统计正整数的个数

7、代码​

function minimumOperations(nums: number[]): number {
    const set = new Set(nums);
    return set.size - (set.has(0) ? 1 : 0);
};

或者这样

function minimumOperations(nums: number[]): number {
    return new Set(nums.filter(Boolean)).size;
};

8、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

9、执行结果​

1、题干​

现有一台饮水机，可以制备冷水、温水和热水。每秒钟，可以装满 2 杯 不同 类型的水或者 1 杯任意类型的水。

给你一个下标从 0 开始、长度为 3 的整数数组 amount ，其中 amount[0]、amount[1] 和 amount[2] 分别表示需要装满冷水、温水和热水的杯子数量。返回装满所有杯子所需的 最少 秒数。

示例 1：

输入：amount = [1,4,2]
输出：4
解释：下面给出一种方案：
第 1 秒：装满一杯冷水和一杯温水。
第 2 秒：装满一杯温水和一杯热水。
第 3 秒：装满一杯温水和一杯热水。
第 4 秒：装满一杯温水。
可以证明最少需要 4 秒才能装满所有杯子。

示例 2：

输入：amount = [5,4,4]
输出：7
解释：下面给出一种方案：
第 1 秒：装满一杯冷水和一杯热水。
第 2 秒：装满一杯冷水和一杯温水。
第 3 秒：装满一杯冷水和一杯温水。
第 4 秒：装满一杯温水和一杯热水。
第 5 秒：装满一杯冷水和一杯热水。
第 6 秒：装满一杯冷水和一杯温水。
第 7 秒：装满一杯热水。

示例 3：

输入：amount = [5,0,0]
输出：5
解释：每秒装满一杯冷水。

提示：

• amount.length == 3
• 0 <= amount[i] <= 100

2、思路​

假设杯子数量从少到多分别为 min、mid、max，首先得装满最多的杯子，因此存在两种情况：

• min + mid <= max，这种情况只需要 max 秒钟就能装满所有杯子
• min + mid > max，先装满最多的杯子，需要 max 秒钟
  • 另外两种杯子会剩余 min + mid - max 个，剩余杯子可能为奇数也可能为偶数，但两种杯子差值最多为 1，所以还需要 Math.ceil((mid + min - max) / 2) 秒钟

3、代码​

function fillCups(amount: number[]): number {
    const [min, mid, max] = amount.sort((a, b) => a - b);
    if (min + mid <= max) return max;
    return max + Math.ceil((mid + min - max) / 2);
};

4、复杂度​

• 时间复杂度：$O(1)$
• 空间复杂度：$O(1)$

5、执行结果​

1、题干​

力扣公司的员工都使用员工卡来开办公室的门。每当一个员工使用一次他的员工卡，安保系统会记录下员工的名字和使用时间。如果一个员工在一小时时间内使用员工卡的次数大于等于三次，这个系统会自动发布一个 警告 。

给你字符串数组 keyName 和 keyTime ，其中 [keyName[i], keyTime[i]] 对应一个人的名字和他在 某一天 内使用员工卡的时间。

使用时间的格式是 24小时制 ，形如 "HH:MM" ，比方说 "23:51" 和 "09:49" 。

请你返回去重后的收到系统警告的员工名字，将它们按 字典序升序 排序后返回。

请注意 "10:00" - "11:00" 视为一个小时时间范围内，而 "22:51" - "23:52" 不被视为一小时时间范围内。

示例 1：

输入：keyName = ["daniel","daniel","daniel","luis","luis","luis","luis"], keyTime = ["10:00","10:40","11:00","09:00","11:00","13:00","15:00"]
输出：["daniel"]
解释："daniel" 在一小时内使用了 3 次员工卡（"10:00"，"10:40"，"11:00"）。

示例 2：

输入：keyName = ["alice","alice","alice","bob","bob","bob","bob"], keyTime = ["12:01","12:00","18:00","21:00","21:20","21:30","23:00"]
输出：["bob"]
解释："bob" 在一小时内使用了 3 次员工卡（"21:00"，"21:20"，"21:30"）。

提示：

• 1 <= keyName.length, keyTime.length <= 105
• keyName.length == keyTime.length
• keyTime 格式为 "HH:MM" 。
• 保证 [keyName[i], keyTime[i]] 形成的二元对 互不相同 。
• 1 <= keyName[i].length <= 10
• keyName[i] 只包含小写英文字母。

2、思路1​

哈希表存储员工姓名（键）和开门时间数组（值），时间转为分钟数并排序，最后检查每个员工的开门时间是否违规

3、代码​

function alertNames(names: string[], times: string[]): string[] {
    const map = new Map<string, number[]>();
    for (let i = 0; i < names.length; i++) {
        if (!map.has(names[i])) map.set(names[i], []);
        map.get(names[i]).push(60 * (+times[i].slice(0, 2)) + +(times[i].slice(3)));
    }

    const ans = [];
    for (const [name, minutes] of map) {
        if (minutes.length < 3) continue;

        minutes.sort((a, b) => a - b);
        for (let i = 0; i < minutes.length - 2 && ans.at(-1) !== name; i++) {
            if (minutes[i + 2] - minutes[i] <= 60) ans.push(name);
        }
    }

    return ans.sort();
};

4、复杂度​

• 时间复杂度：$O(n*logn)$
• 空间复杂度：$O(n)$

5、执行结果​

6、思路2​

二维数组存储员工姓名和开门时间，时间转为分钟数，对二维数组按姓名和分钟数升序排序，最后检查每个员工的开门时间是否违规

7、代码​

function alertNames(names: string[], times: string[]): string[] {
    const matrix: [string, number][] = names.map((n, i) => [n, 60 * (+times[i].slice(0, 2)) + +(times[i].slice(3))]);
    matrix.sort((a, b) => {
        if (a[0] === b[0]) return a[1] - b[1];
        return a[0] > b[0] ? 1 : -1;
    });

    const ans = [];

    for (let i = 0; i < matrix.length - 2; i++) {
        if (matrix[i + 2][0] !== matrix[i][0] || matrix[i][0] === ans.at(-1)) continue;
        if (matrix[i + 2][1] - matrix[i][1] <= 60) ans.push(matrix[i][0]);
    }

    return ans;
};

8、复杂度​

• 时间复杂度：$O(n*logn)$
• 空间复杂度：$O(n)$

9、执行结果​

1、题干​

一个房间里有 n 个座位和 n 名学生，房间用一个数轴表示。给你一个长度为 n 的数组 seats ，其中 seats[i] 是第 i 个座位的位置。同时给你一个长度为 n 的数组 students ，其中 students[j] 是第 j 位学生的位置。

你可以执行以下操作任意次：

• 增加或者减少第 i 位学生的位置，每次变化量为 1 （也就是将第 i 位学生从位置 x 移动到 x + 1 或者 x - 1）

请你返回使所有学生都有座位坐的 最少移动次数 ，并确保没有两位学生的座位相同。

请注意，初始时有可能有多个座位或者多位学生在 同一 位置。

示例 1：

输入：seats = [3,1,5], students = [2,7,4]
输出：4
解释：学生移动方式如下：
- 第一位学生从位置 2 移动到位置 1 ，移动 1 次。
- 第二位学生从位置 7 移动到位置 5 ，移动 2 次。
- 第三位学生从位置 4 移动到位置 3 ，移动 1 次。
总共 1 + 2 + 1 = 4 次移动。

示例 2：

输入：seats = [4,1,5,9], students = [1,3,2,6]
输出：7
解释：学生移动方式如下：
- 第一位学生不移动。
- 第二位学生从位置 3 移动到位置 4 ，移动 1 次。
- 第三位学生从位置 2 移动到位置 5 ，移动 3 次。
- 第四位学生从位置 6 移动到位置 9 ，移动 3 次。
总共 0 + 1 + 3 + 3 = 7 次移动。

示例 3：

输入：seats = [2,2,6,6], students = [1,3,2,6]
输出：4
解释：学生移动方式如下：
- 第一位学生从位置 1 移动到位置 2 ，移动 1 次。
- 第二位学生从位置 3 移动到位置 6 ，移动 3 次。
- 第三位学生不移动。
- 第四位学生不移动。
总共 1 + 3 + 0 + 0 = 4 次移动。

提示：

• n == seats.length == students.length
• 1 <= n <= 100
• 1 <= seats[i], students[j] <= 100

2、思路​

排序后累加差值

3、代码​

function minMovesToSeat(seats: number[], students: number[]): number {
    seats.sort((a, b) => a - b);
    students.sort((a, b) => a - b);
    return seats.reduce((a, c, i) => a + Math.abs(c - students[i]), 0);
};

4、复杂度​

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(1)$