25 篇博文 含有标签「广度优先搜索」

1、题干​

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

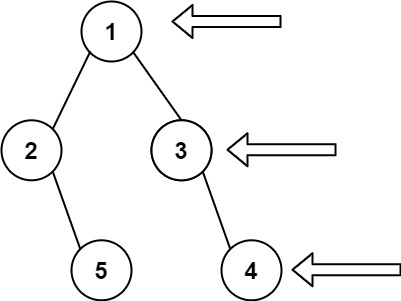
输入: root = [2,1,3]
输出: 1

示例 2:

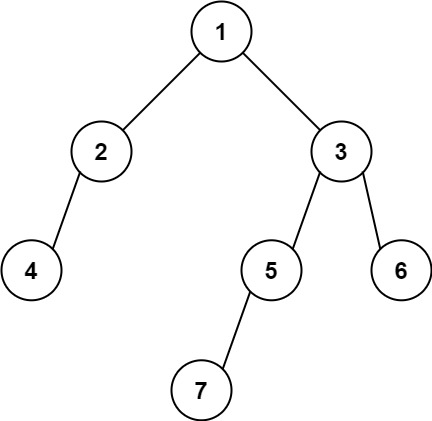
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

• 二叉树的节点个数的范围是 [1,104]
• -231 <= Node.val <= 231 - 1 

执行结果​

解题思路​

总体思路：使用DFS递归遍历树的所有节点，当第一次遍历到层级大于所有已遍历节点的节点时，该节点就是当前层级的最左子节点；随着遍历层级递增，最终能找到最底层的最左子节点。

• 使用DFS递归遍历树的所有节点
• 记录当前节点的层级level与已遍历节点的最大层级maxLevel
• 每当level超过maxLevel时，将当前节点赋值给res，另外更新maxLevel
• 遍历完成后，res就是要找的节点，返回该节点的值即可

代码​

var findBottomLeftValue = function (root) {
    let res, maxLevel = 0;
    function dfs(node, level) {
        if (!node) return;
        if (level > maxLevel) res = node, maxLevel = level;
        dfs(node.left, level + 1);
        dfs(node.right, level + 1);
    }
    dfs(root, 1);
    return res && res.val;
};

1、题干​

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

• 二叉树的节点个数的范围是 [0,100]
• -100 <= Node.val <= 100 

执行结果​

解题思路​

总体思路：使用DFS递归遍历树的所有节点，创建结果数组res，将当前节点的层级当做res的下标、val当做res的值，以此更新res，右边节点的值会不断覆盖左边节点，得到的数组就是从右侧所能看到的节点值。

代码​

var rightSideView = function (root) {
    const res = [];
    function dfs(node, level) {
        if (!node) return;
        res[level] = node.val;
        dfs(node.left, level + 1);
        dfs(node.right, level + 1);
    }
    dfs(root, 0);
    return res;
};

1、题干​

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] 的值为 '0' 或 '1'

解题思路​

• 遍历矩阵grid，以grid[i][j]为起点往上下左右4个方向进行深度遍历
• 深度遍历过程中需要注意2点
  • 遍历过的节点修改为0，即grid[i][j] = '0'，以免重复遍历
  • grid[i][j]必须在矩阵中且grid[i][j] === '1'才累加岛屿数量

代码​

var numIslands = function (grid) {
    const dirs = [[0, 1], [0, -1], [1, 0], [-1, 0]];
    function dfs(i, j) {
        if (i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] === '0') return false;
        grid[i][j] = '0';
        for (const [di, dj] of dirs) dfs(i + di, j + dj);
        return true;
    }

    let count = 0;
    for (let i = 0; i < grid.length; i++) {
        for (let j = 0; j < grid[i].length; j++) {
            if (dfs(i, j)) count++;
        }
    }

    return count;
};

1、题干​

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程  bi 。

• 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

• 1 <= numCourses <= 2000
• 0 <= prerequisites.length <= 5000
• prerequisites[i].length == 2
• 0 <= ai, bi < numCourses
• prerequisites[i] 中的所有课程对 互不相同

2、解题思路​

题干很长，浓缩下就简单很多：给一个有向图，判定其中是否有环 。总的思路是 BFS 或 DFS 遍历整个图，如果存在环则返回 false，否则返回 true。

• 第一步 ：把先修课程 prerequisites 转换为二维数组，即用二维数组存储图的信息
  • 创建二维数组 edges 来表示先修课程，下标表示课程，内层数组表示先修课程集合
  • edges[i] 中的下标 i 表示课程 i ，edges[i] 表示课程i的先修课程集合
  • edges[i][j] 表示课程 i 的一个先修课程，edges[i][j] 的值是 edges 的一个下标

• 第二步 ：按课程序号从0开始深度遍历edges，判定图中是否存在环

• 第三步 ：以任意课程 c 为起始点深度遍历其先修课程，过程中注意3点：
  • 所有遍历过的节点使用哈希集合 visited 记录，以达到剪枝效果避免超时
  • 当前路径遍历过的节点使用哈希集合 paths 记录，如果当前节点已存在于 paths 中，说明存在环
  • 如果课程 c2 后续路径合法，记得将其从 paths 中移除，以免干扰其他路径遍历（类似回溯中的状态重置）

3、复杂度​

• 时间复杂度: $O(n)$
• 空间复杂度: $O(n)$

4、代码​

var canFinish = function (numCourses, prerequisites) {
    // 1、把先修课程`prerequisites`转换为二维数组表示的图
    const edges = new Array(numCourses).fill(0).map(() => []);
    for (let p of prerequisites) edges[p[1]].push(p[0]);

    // 以课程c为起始点，深度遍历所有先修课程
    const visited = new Set();
    function dfs(c, paths) {
        if (visited.has(c)) return false;
        visited.add(c);

        paths.add(c);
        for (const c2 of edges[c]) {
            if (paths.has(c2) || dfs(c2, paths)) return true;
            paths.delete(c2);
        }

        return false;
    }

    // 2、按课程序号从0开始深度遍历`edges`，判定图中是否存在环
    for (let i = 0; i < edges.length; i++) {
        if (dfs(i, new Set())) return false;
    }

    return true;
};

1、题干​

给你一个下标从 0 开始的整数数组 nums ，该数组由 互不相同 的数字组成。另给你两个整数 start 和 goal 。

整数 x 的值最开始设为 start ，你打算执行一些运算使 x 转化为 goal 。你可以对数字 x 重复执行下述运算：

如果 0 <= x <= 1000 ，那么，对于数组中的任一下标 i（0 <= i < nums.length），可以将 x 设为下述任一值：

• x + nums[i]
• x - nums[i]
• x ^ nums[i]（按位异或 XOR）

注意，你可以按任意顺序使用每个 nums[i] 任意次。使 x 越过 0 <= x <= 1000 范围的运算同样可以生效，但该该运算执行后将不能执行其他运算。

返回将 x = start 转化为 goal 的最小操作数；如果无法完成转化，则返回 -1 。

示例 1：

输入：nums = [2,4,12], start = 2, goal = 12
输出：2
解释：
可以按 2 → 14 → 12 的转化路径进行，只需执行下述 2 次运算：
- 2 + 12 = 14
- 14 - 2 = 12

示例 2：

输入：nums = [3,5,7], start = 0, goal = -4
输出：2
解释：
可以按 0 → 3 → -4 的转化路径进行，只需执行下述 2 次运算：
- 0 + 3 = 3
- 3 - 7 = -4
注意，最后一步运算使 x 超过范围 0 <= x <= 1000 ，但该运算仍然可以生效。

示例 3：

输入：nums = [2,8,16], start = 0, goal = 1
输出：-1
解释：
无法将 0 转化为 1

提示：

• 1 <= nums.length <= 1000
• -109 <= nums[i], goal <= 109
• 0 <= start <= 1000
• start != goal
• nums 中的所有整数互不相同

解题思路​

• 把 start 看做树的根节点
• start 与 nums 进行 +-^ 三种操作的结果看做第一层子节点
• 依此类推可以构建出一棵树
• 题目要求找到 start 转化为 goal 的最小操作数，实际就是在整颗树中找到 goal 所在的层数
• 所以采用 BFS 方式进行查找，过程中注意处理边界条件、减少耗时操作，以免死循环或超时

代码​

/**
 * @param {number[]} nums
 * @param {number} start
 * @param {number} goal
 * @return {number}
 */
var minimumOperations = function(nums, start, goal) {
    const queueMatrix = [[start]];
    let count = 0;
    const set = new Set();

    while (queueMatrix.length) {
        const queue = queueMatrix.shift();
        count += 1;
        const newQueue = [];

        for (let k = 0; k < queue.length; k++) {
            start = queue[k];
            if (start < 0 || start > 1000 || set.has(start)) continue;

            set.add(start);
            for (let i = 0; i < nums.length; i++) {
                const n1 = start + nums[i];
                const n2 = start - nums[i];
                const n3 = start ^ nums[i];
                newQueue.push(n1);
                newQueue.push(n2);
                newQueue.push(n3);

                if (n1 === goal || n2 === goal || n3 === goal) return count;
            }
        }

        if (newQueue.length) queueMatrix.push(newQueue);
    }

    return -1;
};