1、题干
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
示例 1:
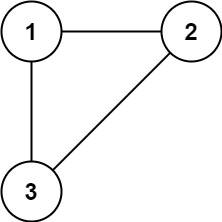
输入: edges = [[1,2],[1,3],[2,3]]
输出: [2,3]
示例 2:
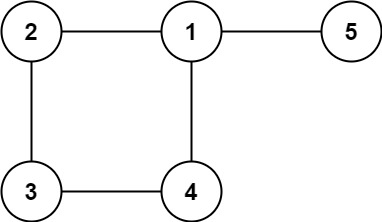
输入: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
输出: [1,4]
提示:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ai < bi <= edges.lengthai != biedges中无重复元素- 给定的图是连通的
注意:本题与主站 684 题相同: https://leetcode-cn.com/problems/redundant-connection/
并查集还没学会,只能先用树和图的思想解题

2、解题思路
在树的概念中,叶子结点是指没有子结点的结点,叶子节点只跟父节点存在关联,即只有1条边。如果某个节点下只有叶子节点,把该节点下的所有叶子节点都移除掉之后它自己就变成了叶子节点。如果循环往复地移除树的所有叶子节点,最终这棵树的节点数会变为0 。
如果按题目意思在树中添加一条边,这棵树会变成一个有环图,而在移除所有叶子节点的操作中,环上的所有节点都不会被移除,本题就是利用这个结论解题。
总体思路 :循环往复地移除树上所有的叶子节点,直到不存在叶子节点,最后遍历找到环中最后出现的边。
大体步骤 :
- 先用矩阵建立节点关联关系,记为
matrixmatrix是一维数组,下标表示节点值matrix中的元素是哈希集合,集合中包含与当前节点关联的所有节点
- 遍历
matrix并把当前节点加入队列queue中,进行叶子节点的判断与移除- 若该节点是叶子节点,则双向移除该节点与父节点的关联关系,同时把父节点加入队列
queue中进行下一轮处理 - 若该节点不是叶子节点则跳过
- 若该节点是叶子节点,则双向移除该节点与父节点的关联关系,同时把父节点加入队列
- 最后遍历二维数组
edges并在matrix中查找出处于环上且序号最大的边
3、代码
var findRedundantConnection = function (edges) {
const n = edges.length, matrix = new Array(n + 1).fill(0);
for (const [i, j] of edges) {
!matrix[i] ? (matrix[i] = new Set([j])) : matrix[i].add(j);
!matrix[j] ? (matrix[j] = new Set([i])) : matrix[j].add(i);
}
for (let k = 1; k <= n; k++) {
const queue = [k];
for (const i of queue) {
if (matrix[i].size !== 1) continue;
const j = matrix[i].keys().next().value;
matrix[i].delete(j), matrix[j].delete(i);
queue.push(j);
}
}
return edges.reduce((a, [i, j]) => (matrix[i].size > 1 && matrix[j].size > 1 ? [i, j] : a), null);
};
4、复杂度
- 时间复杂度:,复杂度比较高的代码在双层循环剪叶子那一段,外层循环 次,内层循环最多为树的高度 次
- 空间复杂度:
5、执行结果
- 执行用时: 68 ms
- 内存消耗: 42.1 MB