1、题干​

给定字符串 s 和字符串数组 words, 返回  words[i] 中是s的子序列的单词个数 。

字符串的 子序列 是从原始字符串中生成的新字符串，可以从中删去一些字符(可以是none)，而不改变其余字符的相对顺序。

• 例如， “ace” 是 “abcde” 的子序列。

示例 1:

输入: s = "abcde", words = ["a","bb","acd","ace"]
输出: 3
解释: 有三个是 s 的子序列的单词: "a", "acd", "ace"。

Example 2:

输入: s = "dsahjpjauf", words = ["ahjpjau","ja","ahbwzgqnuk","tnmlanowax"]
输出: 2

提示:

• 1 <= s.length <= 5 * 104
• 1 <= words.length <= 5000
• 1 <= words[i].length <= 50
• words[i]和s 都只由小写字母组成。

Problem: 792. 匹配子序列的单词数

2、思路​

二分查找

• 按字母表顺序把字符串 s 中所有字符的下标升序存入二维数组 idxMatrix
• 判断数组 words 中任意字符串 w 是否 s 的子序列，只需要判断 w 中任意字符 c 比前一个字符 在 s 中的下标更大。其中查找 c 在 s 中的下标时，使用二分查找算法

3、Code​

function numMatchingSubseq(s: string, words: string[]): number {
    const CA = 'a'.charCodeAt(0), idxMatrix = new Array(26).fill(0).map(() => []);

    for (let i = 0; i < s.length; i++) {
        const ci = s[i].charCodeAt(0) - CA;
        idxMatrix[ci].push(i);
    }

    function find(nums: number[] = [], k: number) {
        let l = 0, r = nums.length - 1;

        while (l <= r) {
            const m = ((l + r) / 2) >> 0;
            if (nums[m] > k) {
                if (nums[m - 1] > k) r = m - 1;
                else return nums[m];
            } else {
                l = m + 1;
            }
        }

        return -1;
    }

    let res = 0;
    loop: for (const w of words) {
        let preIdx = -1;
        for (const c of w) {
            const ci = c.charCodeAt(0) - CA;
            const ni = find(idxMatrix[ci], preIdx);
            if (ni < 0) continue loop;
            preIdx = ni;
        }
        res++;
    }

    return res;
};

4、复杂度​

• 时间复杂度：$O(n*logn)$
• 空间复杂度：$O(n)$

5、执行结果​

1、题干​

给定两个字符串 order 和 s 。order 的所有字母都是 唯一 的，并且以前按照一些自定义的顺序排序。

对 s 的字符进行置换，使其与排序的 order 相匹配。更具体地说，如果在 order 中的字符 x 出现字符 y 之前，那么在排列后的字符串中， x 也应该出现在 y 之前。

返回 满足这个性质的 s 的任意一种排列 。

示例 1:

输入: order = "cba", s = "abcd"
输出: "cbad"
解释: 
“a”、“b”、“c”是按顺序出现的，所以“a”、“b”、“c”的顺序应该是“c”、“b”、“a”。
因为“d”不是按顺序出现的，所以它可以在返回的字符串中的任何位置。“dcba”、“cdba”、“cbda”也是有效的输出。

示例 2:

输入: order = "cbafg", s = "abcd"
输出: "cbad"

提示:

• 1 <= order.length <= 26
• 1 <= s.length <= 200
• order 和 s 由小写英文字母组成
• order 中的所有字符都 不同

Problem: 791. 自定义字符串排序

2、思路​

数量级比较小 order.length <= 26，s.length <= 200，用 Array.sort 实现就行

3、Code​

function customSortString(o: string, s: string): string {
    return [...s].sort((a, b) => o.indexOf(a) - o.indexOf(b)).join('');
};

4、复杂度​

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(n)$

5、执行结果​

1、题干​

给你一个由不同字符组成的字符串 allowed 和一个字符串数组 words 。如果一个字符串的每一个字符都在 allowed 中，就称这个字符串是 一致字符串 。

请你返回 words 数组中 一致字符串 的数目。

示例 1：

输入：allowed = "ab", words = ["ad","bd","aaab","baa","badab"]
输出：2
解释：字符串 "aaab" 和 "baa" 都是一致字符串，因为它们只包含字符 'a' 和 'b' 。

示例 2：

输入：allowed = "abc", words = ["a","b","c","ab","ac","bc","abc"]
输出：7
解释：所有字符串都是一致的。

示例 3：

输入：allowed = "cad", words = ["cc","acd","b","ba","bac","bad","ac","d"]
输出：4
解释：字符串 "cc"，"acd"，"ac" 和 "d" 是一致字符串。

提示：

• 1 <= words.length <= 104
• 1 <= allowed.length <= 26
• 1 <= words[i].length <= 10
• allowed 中的字符 互不相同 。
• words[i] 和 allowed 只包含小写英文字母。

Problem: 1684. 统计一致字符串的数目

[TOC]

思路

reduce 跟 for of 耗费的时间空间差距还挺大

Code - for of

function countConsistentStrings(allowed: string, words: string[]): number {
    const dict = new Set(allowed);
    let res = 0;
    loop: for (const s of words) {
        for (const c of s) {
            if (!dict.has(c)) continue loop;
        }
        res++;
    }
    return res;
};

Code - reduce

function countConsistentStrings(allowed: string, words: string[]): number {
    const dict = new Set(allowed);
    return words.reduce((a, s) => a + +([].every.call(s, (c) => dict.has(c))), 0);
};

1、题干​

我们有一些二维坐标，如 "(1, 3)" 或 "(2, 0.5)"，然后我们移除所有逗号，小数点和空格，得到一个字符串S。返回所有可能的原始字符串到一个列表中。

原始的坐标表示法不会存在多余的零，所以不会出现类似于"00", "0.0", "0.00", "1.0", "001", "00.01"或一些其他更小的数来表示坐标。此外，一个小数点前至少存在一个数，所以也不会出现“.1”形式的数字。

最后返回的列表可以是任意顺序的。而且注意返回的两个数字中间（逗号之后）都有一个空格。

示例 1:
输入: "(123)"
输出: ["(1, 23)", "(12, 3)", "(1.2, 3)", "(1, 2.3)"]

示例 2:
输入: "(00011)"
输出:  ["(0.001, 1)", "(0, 0.011)"]
解释: 
0.0, 00, 0001 或 00.01 是不被允许的。

示例 3:
输入: "(0123)"
输出: ["(0, 123)", "(0, 12.3)", "(0, 1.23)", "(0.1, 23)", "(0.1, 2.3)", "(0.12, 3)"]

示例 4:
输入: "(100)"
输出: [(10, 0)]
解释: 
1.0 是不被允许的。

提示:

• 4 <= S.length <= 12.
• S[0] = "(", S[S.length - 1] = ")", 且字符串 S 中的其他元素都是数字。

Problem: 816. 模糊坐标

[TOC]

思路

• 剔除原始字符串 s 中的括号
• 将 s 拆分成两个字符串 s1、s2
• 分别对 s1、s2 添加小数点，得到两个字符串数组 nums1、nums2
• 组合 nums1、nums2 中的字符串得到最终结果

复杂度

• 时间复杂度：$O(n^3)$
• 空间复杂度：$O(n^3)$

Code

function ambiguousCoordinates(s: string): string[] {
    s = s.slice(1, s.length - 1);

    const res = [];

    function insertDot(str: string) {
        const nums = /^0\d/.test(str) ? [] : [str];

        for (let j = 1; j < str.length; j++) {
            const ns = str.slice(0, j) + '.' + str.slice(j);
            if (!/^0\d|0$/.test(ns)) nums.push(ns);
        }

        return nums;
    }

    for (let i = 1; i < s.length; i++) {
        const s1 = s.slice(0, i), s2 = s.slice(i);
        const nums1 = insertDot(s1), nums2 = insertDot(s2);

        for (const ns1 of nums1) {
            for (const ns2 of nums2) {
                res.push(`(${ns1}, ${ns2})`);
            }
        }
    }

    return res;
}

1、题干​

布尔表达式 是计算结果不是 true 就是 false 的表达式。有效的表达式需遵循以下约定：

• 't'，运算结果为 true
• 'f'，运算结果为 false
• '!(subExpr)'，运算过程为对内部表达式 subExpr 进行 逻辑非（NOT）运算
• '&(subExpr1, subExpr2, ..., subExprn)'，运算过程为对 2 个或以上内部表达式 subExpr1, subExpr2, ..., subExprn 进行 逻辑与（AND）运算
• '|(subExpr1, subExpr2, ..., subExprn)'，运算过程为对 2 个或以上内部表达式 subExpr1, subExpr2, ..., subExprn 进行 逻辑或（OR）运算

给你一个以字符串形式表述的 布尔表达式 expression，返回该式的运算结果。

题目测试用例所给出的表达式均为有效的布尔表达式，遵循上述约定。

示例 1：

输入：expression = "&(|(f))"
输出：false
解释：
首先，计算 |(f) --> f ，表达式变为 "&(f)" 。
接着，计算 &(f) --> f ，表达式变为 "f" 。
最后，返回 false 。

示例 2：

输入：expression = "|(f,f,f,t)"
输出：true
解释：计算 (false OR false OR false OR true) ，结果为 true 。

示例 3：

输入：expression = "!(&(f,t))"
输出：true
解释：
首先，计算 &(f,t) --> (false AND true) --> false --> f ，表达式变为 "!(f)" 。
接着，计算 !(f) --> NOT false --> true ，返回 true 。

提示：

• 1 <= expression.length <= 2 * 104
• expression[i] 为 '('、')'、'&'、'|'、'!'、't'、'f' 和 ',' 之一

Problem: 1106. 解析布尔表达式

[TOC]

思路

使用正则不断提取最小表达式进行计算，再将该表达式替换为计算结果。其中最小表达式就是题干中给出的3种情况："!(expr)"，"&(expr1,expr2,...)"，"|(expr1,expr2,...)"

代码

function parseBoolExpr(exp: string): boolean {
    const T = "t", F = "f", reg = /.\([^()]+\)/g;
    while (reg.test(exp)) {
        exp = exp.replace(reg, (m) => {
            if (m[0] === "&") return m.includes(F) ? F : T;
            if (m[0] === "|") return m.includes(T) ? T : F;
            return m.includes(T) ? F : T;
        });
    }
    return exp.includes(T);
}

结果

1、题干​

神奇字符串 s 仅由 '1' 和 '2' 组成，并需要遵守下面的规则：

• 神奇字符串 s 的神奇之处在于，串联字符串中 '1' 和 '2' 的连续出现次数可以生成该字符串。

s 的前几个元素是 s = "1221121221221121122……" 。如果将 s 中连续的若干 1 和 2 进行分组，可以得到 "1 22 11 2 1 22 1 22 11 2 11 22 ......" 。每组中 1 或者 2 的出现次数分别是 "1 2 2 1 1 2 1 2 2 1 2 2 ......" 。上面的出现次数正是 s 自身。

给你一个整数 n ，返回在神奇字符串 s 的前 n 个数字中 1 的数目。

示例 1：

输入：n = 6
输出：3
解释：神奇字符串 s 的前 6 个元素是 “122112”，它包含三个 1，因此返回 3 。 

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 105

2、解题思路​

题目要求计算神奇字符串 s 的前 n 个数字中 1 的数目，只需要按照规则模拟构造神奇字符串，再计算 1 的数量即可。

构造过程借助双指针实现，快指针 i 逐步递增，慢指针 cur 根据其可消耗次数 count 决定是否递增，每次 i 递增做以下计算：

• 若当前字符是 1，则最终结果累计一次
• 计算出第 i+1 个字符，第 i+1 个字符只有两种情况，要么跟第 i 个字符相同，要么不同
  • 当前仅当慢指针 cur 对应的字符是 2 且 第 i-1 和 i 个字符不同时，第 i 和 i+1 个字符相同
  • 其他情况第 i 和 i+1 个字符不同
• 可消耗次数 count 减 1
• 若可消耗次数 count 次数为 0，那么慢指针 cur 加 1，count 赋值为慢指针指向的新数字

3、代码​

function magicalString(n: number): number {
    const nums = new Array(n).fill(1);
    let res = 0, cur = 0, count = 1;

    for (let i = 0; i < n; i++) {
        if (nums[i] === 1) res++;

        nums[i + 1] = nums[i] === 2 ? 1 : 2;
        if (nums[cur] === 2 && nums[i] !== nums[i - 1]) nums[i + 1] = nums[i];

        if (--count === 0) count = nums[++cur];
    }

    return res;
}

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

5、执行结果​

1、题干​

字符串有三种编辑操作:插入一个英文字符、删除一个英文字符或者替换一个英文字符。 给定两个字符串，编写一个函数判定它们是否只需要一次(或者零次)编辑。

示例 1:

输入: 
first = "pale"
second = "ple"
输出: True

示例 2:

输入: 
first = "pales"
second = "pal"
输出: False

2、解题思路​

顺序遍历统计左半边相同字符总数 sl，倒序遍历统计右半边相同字符总数 sr，两字符串最大长度与 sl + sr 之差不大于 $1$ 则返回 true，否则返回 false。

两个字符串长度差值大于 $1$ 则直接返回 false，这一前置判断可有可无

3、代码​

var oneEditAway = function (first, second) {
    if (Math.abs(first.length - second.length) > 1) return false;

    let sl = 0, sr = 0, m = first.length, n = second.length;
    for (let i = 0; i < Math.min(m, n) && first[i] === second[i]; i++) sl++;
    for (let i = m - 1, j = n - 1; sl - 1 < Math.min(i, j) && first[i] === second[j]; i--, j--) sr++;

    return Math.max(m, n) - sl - sr <= 1;
};

4、执行结果​

• 执行用时: 64 ms
• 内存消耗: 42.7 MB

1、题干​

给你一个长桌子，桌子上盘子和蜡烛排成一列。给你一个下标从 0 开始的字符串 s ，它只包含字符 '*' 和 '|' ，其中 '*' 表示一个 盘子 ，'|' 表示一支 蜡烛 。

同时给你一个下标从 0 开始的二维整数数组 queries ，其中 queries[i] = [lefti, righti] 表示 子字符串 s[lefti...righti] （包含左右端点的字符）。对于每个查询，你需要找到 子字符串中 在 两支蜡烛之间 的盘子的 数目 。如果一个盘子在 子字符串中 左边和右边 都 至少有一支蜡烛，那么这个盘子满足在 两支蜡烛之间 。

• 比方说，s = "||**||**|*" ，查询 [3, 8] ，表示的是子字符串 "*||**|" 。子字符串中在两支蜡烛之间的盘子数目为 2 ，子字符串中右边两个盘子在它们左边和右边 都 至少有一支蜡烛。

请你返回一个整数数组 answer ，其中 answer[i] 是第 i 个查询的答案。

示例 1:

输入：s = "**|**|***|", queries = [[2,5],[5,9]]
输出：[2,3]
解释：
- queries[0] 有两个盘子在蜡烛之间。
- queries[1] 有三个盘子在蜡烛之间。

示例 2:

输入：s = "***|**|*****|**||**|*", queries = [[1,17],[4,5],[14,17],[5,11],[15,16]]
输出：[9,0,0,0,0]
解释：
- queries[0] 有 9 个盘子在蜡烛之间。
- 另一个查询没有盘子在蜡烛之间。

提示：

• 3 <= s.length <= 105
• s 只包含字符 '*' 和 '|' 。
• 1 <= queries.length <= 105
• queries[i].length == 2
• 0 <= lefti <= righti < s.length

2、解题思路​

按题目意思要查找任意区间 [i,j] 内两支蜡烛之间的盘子数量，要解决两个核心问题：

• 1、查找区间 [i,j] 内最左边和最右边蜡烛的下标 [l,r]
• 2、求出区间 [l,r] 内的蜡烛数量

问题1采用区间映射解决，使用二维数组 ranges 存储离任意下标 i 最近的左右蜡烛下标，形如 ranges[i] = [li,ri]。对于任意区间 [i,j] 内最左边和最右边蜡烛的下标为 l = ranges[i][1], r = ranges[j][0]

特殊情况 :

• 左边没有蜡烛时有 ranges[i] = [-1,ri]
• 右边没有蜡烛时有 ranges[i] = [li,s.length]
• 该位置是蜡烛时有 ranges[i] = [i,i]

问题2采用前缀和解决，使用数组 sumList 存储蜡烛数量前缀和，对于任意下标 i 而言 sumList[i] 表示 s[0] 到 s[i] 之间的蜡烛数量。对于任意区间 [l,r] 内的蜡烛数量为 sumList[r] - sumList[l]

至此两个核心问题都得以解决，且都能在 $O(1)$ 时间复杂度内求出正解

3、代码​

var platesBetweenCandles = function (s, queries) {
    const n = s.length, sumList = new Array(n), ranges = new Array(n);
    let ps = 0, range = [-1, n];

    for (let i = 0; i < n; i++) {
        if (s[i] === '*') {
            ps += 1;
            ranges[i] = range;
        } else {
            range[1] = i;
            ranges[i] = [i, i];
            range = [i, n];
        }

        sumList[i] = ps;
    }

    return queries.map(([i, j]) => {
        const l = ranges[i][1], r = ranges[j][0];
        return l > -1 && r < n && l < r ? sumList[r] - sumList[l] : 0;
    });
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

5、执行结果​

• 执行用时: 308 ms
• 内存消耗: 86.1 MB

1、题干​

给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。

返回所有可能的结果。答案可以按 任意顺序 返回。

示例 1：

输入：s = "()())()"
输出：["(())()","()()()"]

示例 2：

输入：s = "(a)())()"
输出：["(a())()","(a)()()"]

示例 3：

输入：s = ")("
输出：[""]

提示：

• 1 <= s.length <= 25
• s 由小写英文字母以及括号 '(' 和 ')' 组成
• s 中至多含 20 个括号

深圳阿里Lazada笔试题T4，30min钟4道题，这道题没时间写

2、解题思路​

回溯+剪枝枚举所有可行的情况，遍历过程中判断合法子串只需要判断已选子串长度不为0且左括号被消耗完即 lc=0，详细逻辑见注释

3、代码​

var removeInvalidParentheses = function (s) {
    let res = [''];

    // 初始状态：字符串下标i，已选字符数组chars，左括号数量lc
    function backtrace(i, chars, lc) {
        // 合法子串，比较长度并填入最终结果
        if (!lc && chars.length && chars.length > res[0].length) res = [chars.join('')];
        else if (!lc && chars.length && chars.length === res[0].length) res.push(chars.join(''));

        // 下标越界，遍历结束
        if (i >= s.length - 1) return;

        // 遍历所有待选字符
        for (let j = i + 1; j < s.length; j++) {
            const c = s[j];
            // 剪枝：存在无法配对的右括号
            if (c === ')' && !lc) continue;
            // 剪枝：1、左括号比剩余子串更长；2、已选子串长度加上未遍历子串长度还是小于结果子串的长度
            if (lc > s.length - j || chars.length + s.length - j < res[0].length) break;

            // 选择当前字符
            chars.push(c);
            // 递归搜索
            backtrace(j, chars, c === '(' ? lc + 1 : (c === ')' ? lc - 1 : lc));
            // 撤销选择
            chars.pop();
        }
    }

    // 初始状态：字符串下标i为-1，已选字符数组chars为空数组，左括号数量lc为0
    backtrace(-1, [], 0);

    return [...new Set(res)];
};

4、执行结果​

1、题干​

给定一个表示整数的字符串 n ，返回与它最近的回文整数（不包括自身）。如果不止一个，返回较小的那个。

“最近的”定义为两个整数差的绝对值最小。

示例 1:

输入: n = "123"
输出: "121"

示例 2:

输入: n = "1"
输出: "0"
解释: 0 和 2是最近的回文，但我们返回最小的，也就是 0。

提示:

• 1 <= n.length <= 18
• n 只由数字组成
• n 不含前导 0
• n 代表在 [1, 1018 - 1] 范围内的整数

2、解题思路​

• 找到中轴并提取中轴前的数字作为前半段，计算前半段数字加1、减1、不变3种情况的结果
• 根据3种计算结果推导3个回文数，对进位导致位数增加、借位导致位数减少、前导0等情况分别进行处理
  • 若进位导致位数增加，求得 10...01 形式的回文数
  • 若借位导致位数减少或出现前导0的情况，求得 99...99 形式的回文数
  • 否则将前半段翻转作为后半段（原数字长度为奇数的需要剔除中轴），求得前后两段拼接而成的回文数
• 在3个回文数中找到与 n 的差值的绝对值最小的数，若存在多个则取较小那个数，最后返回该数

3、代码​

var nearestPalindromic = function (n) {
    const len = n.length, m = Math.floor((len - 1) / 2);
    const s1 = n.slice(0, m + 1);

    const reverse = (s) => [].reduce.call(s, (a, c) => c + a, '');
    const nums = [`${+s1 + 1}`, s1, `${+s1 - 1}`].map((a) => {
        if (a.length > m + 1) return `1${'0'.repeat(len - 1)}1`;
        if (a.length <= m || (a === '0' && len === 2)) return '9'.repeat(len - 1);
        return a + (len % 2 ? reverse(a).slice(1) : reverse(a));
    });
    const diffs = nums.map((d) => BigInt(d) - BigInt(n)).map((d) => (d > 0 ? d : -d));
    const minDiff = diffs.reduce((a, c, i) => (c && c <= a[0] ? [c, i] : a), [Infinity, -1]);
    return nums[minDiff[1]];
};

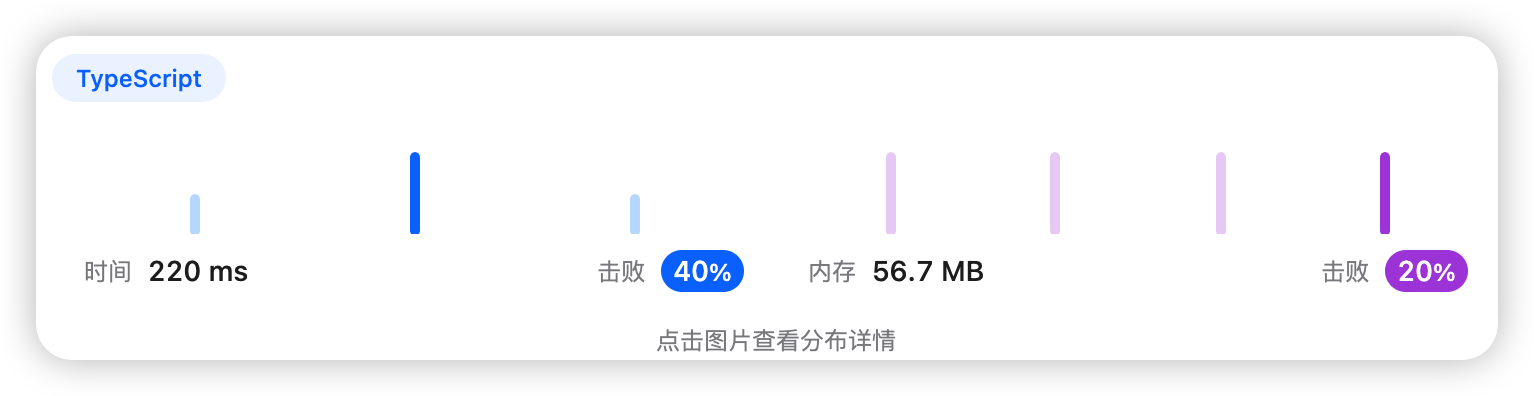
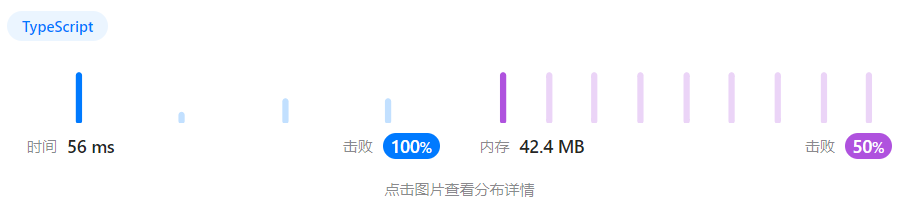
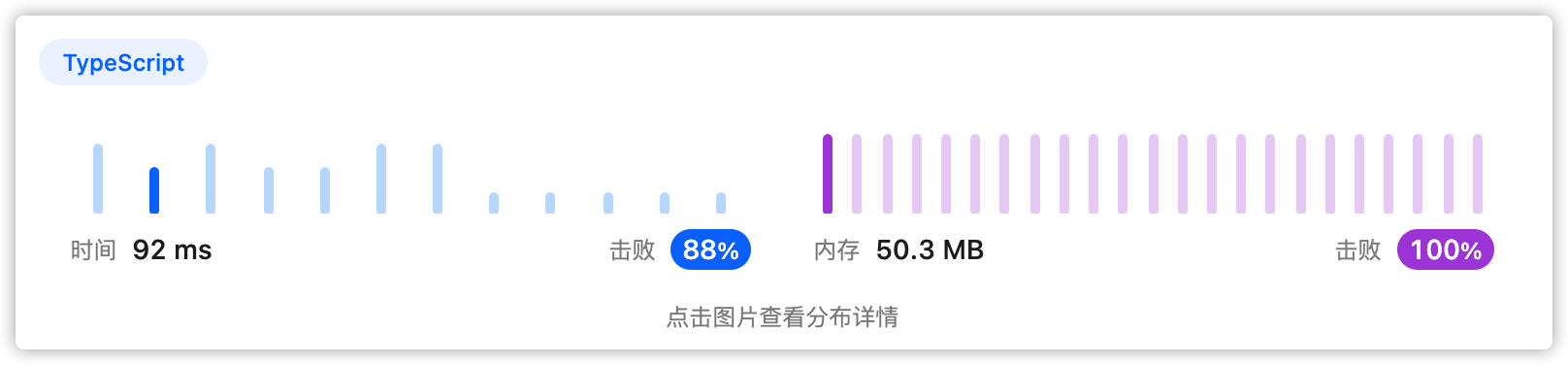
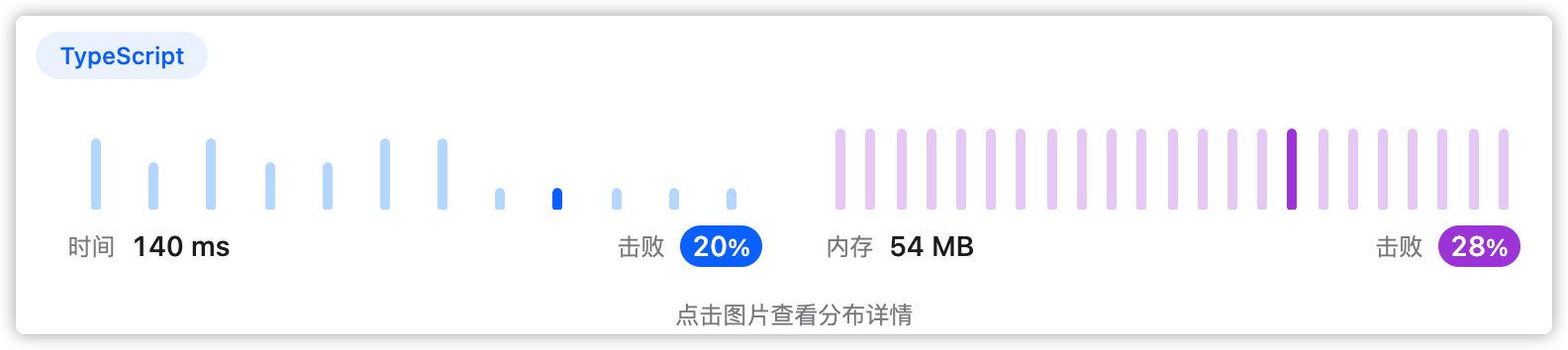
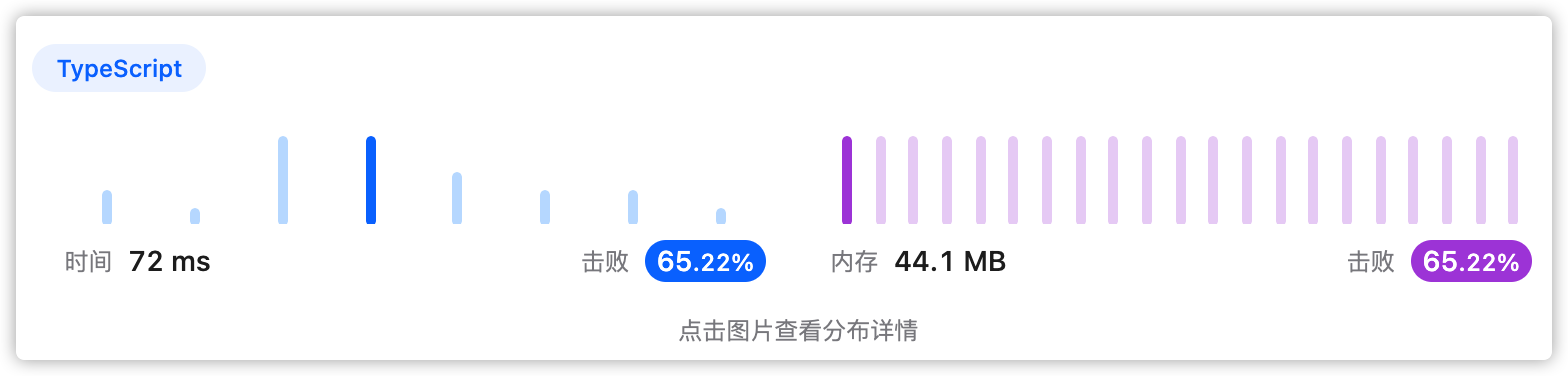
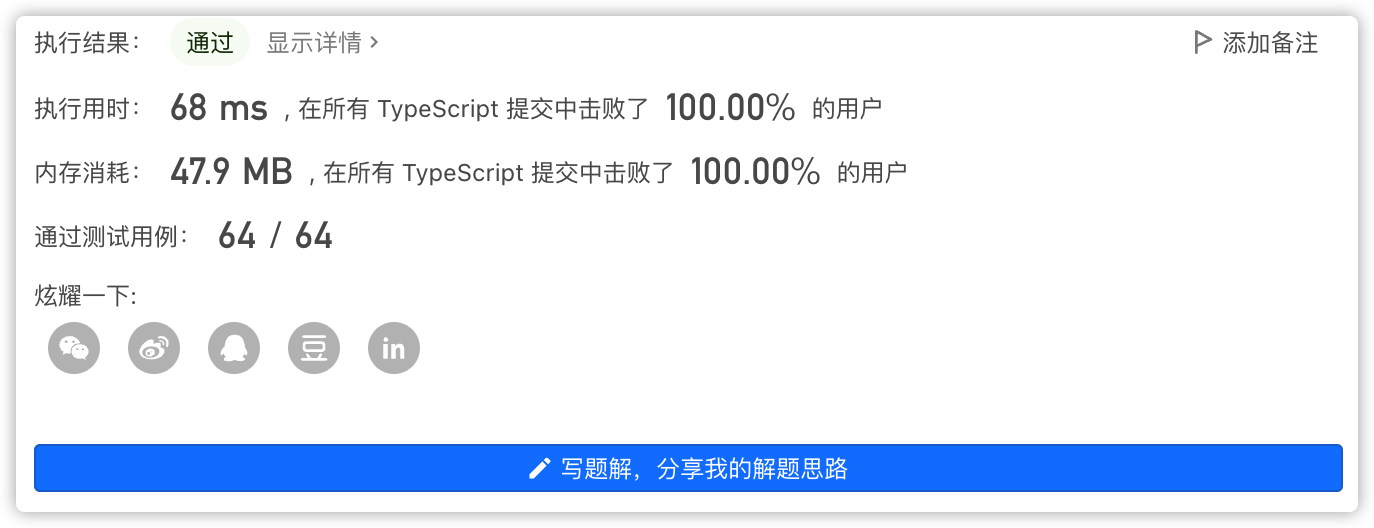
4、执行结果​