8 篇博文含有标签「图」

1、题干

n 座城市和一些连接这些城市的道路 roads 共同组成一个基础设施网络。每个 roads[i] = [a_i, b_i] 都表示在城市 a_i 和 b_i 之间有一条双向道路。

两座不同城市构成的 城市对 的 网络秩 定义为：与这两座城市直接相连的道路总数。如果存在一条道路直接连接这两座城市，则这条道路只计算一次。

整个基础设施网络的 最大网络秩 是所有不同城市对中的 最大网络秩 。

给你整数 n 和数组 roads，返回整个基础设施网络的 最大网络秩 。

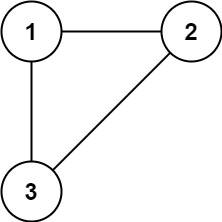
示例 1：

输入：n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
输出：4
解释：城市 0 和 1 的网络秩是 4，因为共有 4 条道路与城市 0 或 1 相连。位于 0 和 1 之间的道路只计算一次。

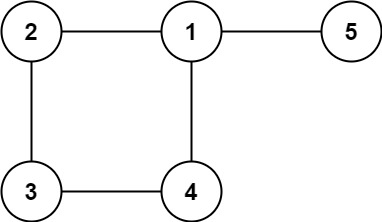
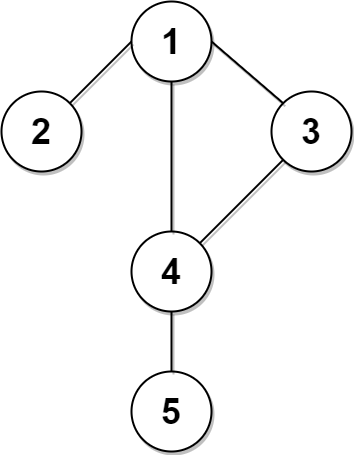
示例 2：

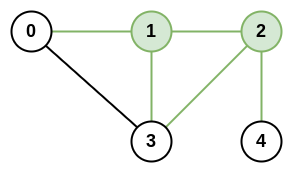
输入：n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
输出：5
解释：共有 5 条道路与城市 1 或 2 相连。

示例 3：

输入：n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
输出：5
解释：2 和 5 的网络秩为 5，注意并非所有的城市都需要连接起来。

提示：

2 <= n <= 100
0 <= roads.length <= n * (n - 1) / 2
roads[i].length == 2
0 <= a_i, b_i <= n-1
a_i != b_i
每对城市之间 最多只有一条 道路相连

2、思路

枚举所有 城市对 的网络秩，取最大值。需要注意，不连通的城市也需要枚举，连通城市对的网络秩需要减1剔除重复。

3、代码

function maximalNetworkRank(n: number, roads: number[][]): number {
    const edges = Array.from({ length: n }, () => new Set<number>());
    for (const [u, v] of roads) {
        edges[u].add(v), edges[v].add(u);
    }

    let ans = 0;
    for (let u = 0; u < n; u++) {
        for (let v = u + 1; v < n; v++) {
            ans = Math.max(ans, edges[u].size + edges[v].size - (edges[u].has(v) ? 1 : 0));
        }
    }

    return ans;
};

4、复杂度

时间复杂度： $O(n^2)$
空间复杂度： $O(n^2)$

5、执行结果

1、题干

给定一个整数 n，即有向图中的节点数，其中节点标记为 0 到 n - 1。图中的每条边为红色或者蓝色，并且可能存在自环或平行边。

给定两个数组 redEdges 和 blueEdges，其中：

redEdges[i] = [a_i, b_i] 表示图中存在一条从节点 a_i 到节点 b_i 的红色有向边，
blueEdges[j] = [u_j, v_j] 表示图中存在一条从节点 u_j 到节点 v_j 的蓝色有向边。

返回长度为 n 的数组 answer，其中 answer[X] 是从节点 0 到节点 X 的红色边和蓝色边交替出现的最短路径的长度。如果不存在这样的路径，那么 answer[x] = -1。

示例 1：

输入：n = 3, red_edges = [[0,1],[1,2]], blue_edges = []
输出：[0,1,-1]

示例 2：

输入：n = 3, red_edges = [[0,1]], blue_edges = [[2,1]]
输出：[0,1,-1]

提示：

1 <= n <= 100
0 <= redEdges.length, blueEdges.length <= 400
redEdges[i].length == blueEdges[j].length == 2
0 <= a_i, b_i, u_j, v_j < n

2、思路

整体思路分为 建表 和 BFS 两步：

建表：将所有邻接点关系存入二维矩阵，第一维下标表示出发点，第二维元素表示到达点，到达点使用正负数表示红蓝两种状态
BFS：广度优先搜索所有可能存在的红蓝交替路径，找出最短路径

3、代码

function shortestAlternatingPaths(n: number, redEdges: number[][], blueEdges: number[][]): number[] {
    const edges: Set<number>[] = new Array(n).fill(0).map(() => new Set());
    for (const [e0, e1] of redEdges) edges[e0].add(e1);
    for (const [e0, e1] of blueEdges) edges[e0].add(-e1);

    const ans = new Array(n).fill(Infinity);
    let nodes = edges[0], visited = new Set([0]);

    for (let depth = 1; nodes.size; depth++) {
        const nextNodes: Set<number> = new Set();

        for (const n of nodes) {
            if (visited.has(n)) continue;
            visited.add(n);

            const i = n < 0 ? -n : n;
            ans[i] = Math.min(ans[i], depth);

            for (const e of edges[i]) {
                if (Math.sign(n) !== Math.sign(e)) nextNodes.add(e);
            }
        }

        nodes = nextNodes;
    }

    return ans[0] = 0, ans.map(a => a === Infinity ? -1 : a);
}

4、复杂度

时间复杂度： $O(n)$
空间复杂度： $O(n)$

5、执行结果

1、题干

有一个需要密码才能打开的保险箱。密码是 n 位数, 密码的每一位都是范围 [0, k - 1] 中的一个数字。

保险箱有一种特殊的密码校验方法，你可以随意输入密码序列，保险箱会自动记住 最后 n 位输入 ，如果匹配，则能够打开保险箱。

例如，正确的密码是 "345" ，并且你输入的是 "012345" ：
- 输入 0 之后，最后 3 位输入是 "0" ，不正确。
- 输入 1 之后，最后 3 位输入是 "01" ，不正确。
- 输入 2 之后，最后 3 位输入是 "012" ，不正确。
- 输入 3 之后，最后 3 位输入是 "123" ，不正确。
- 输入 4 之后，最后 3 位输入是 "234" ，不正确。
- 输入 5 之后，最后 3 位输入是 "345" ，正确，打开保险箱。

在只知道密码位数 n 和范围边界 k 的前提下，请你找出并返回确保在输入的 某个时刻 能够打开保险箱的任一最短密码序列。

示例 1：

输入：n = 1, k = 2
输出："10"
解释：密码只有 1 位，所以输入每一位就可以。"01" 也能够确保打开保险箱。

示例 2：

输入：n = 2, k = 2
输出："01100"
解释：对于每种可能的密码：
- "00" 从第 4 位开始输入。
- "01" 从第 1 位开始输入。
- "10" 从第 3 位开始输入。
- "11" 从第 2 位开始输入。
因此 "01100" 可以确保打开保险箱。"01100"、"10011" 和 "11001" 也可以确保打开保险箱。

提示：

1 <= n <= 4
1 <= k <= 10
1 <= kⁿ <= 4096

2、思路1

题意

题目要找一个能打开保险箱的最短字符串，实际是想找一个所有密码组合而成的最短字符串，该字符串的特征是：截取其中任意长度为 n 的字符串都是保险箱的密码。

思路

先找出所有密码串，再用所有密码串组合出最短字符串。

找出所有密码时要注意，任一密码串长度都为 n，每一位的取值范围是 $[0,k-1]$ 。

组合最短字符串时要注意，在组合任意两个密码串 a 和 b 时，必须满足 a 剔除首位字符后与 b 剔除末位字符后相等。举个例子：

012 与 123 可以组合，因为 012 剔除首位后与 123 剔除末位后都是 12
012 与 213 则不能组合

代码主要逻辑：
- 先找出所有可能的密码串 pwds
- 将所有密码串按前缀分组存入哈希表 pwdMap，前缀指的是剔除密码末位字符之后的字符串
- 使用回溯组合所有密码串
- 所有密码串都用完则顺序拼接并返回

3、代码

function crackSafe(n: number, k: number): string {
    if (k === 1) return '0'.padStart(n, '0');

    // 生成pwds
    const pwds = new Array(k ** n).fill('0').map((v, i) => {
        return k < 2 ? v : i.toString(k).padStart(n, "0");
    });

    if (n === 1) return pwds.join('');

    const pwdMap = new Map();
    for (const p of pwds) {
        const prefix = p.slice(0, n - 1);
        if (!pwdMap.has(prefix)) pwdMap.set(prefix, []);
        pwdMap.get(prefix).push(p);
    }

    // 组合pwds
    let ans = '';
    function dfs(cur: string, used: Set<string>) {
        if (ans) return;
        if (used.size === pwds.length) {
            const nums = [...used];
            ans = nums[0] + nums.slice(1).map(w => w.slice(-1)).join('');
            return;
        }

        const nums = pwdMap.get(cur.slice(1));
        for (const n of nums) {
            if (used.has(n)) continue;
            used.add(n);
            dfs(n, used);
            used.delete(n);
        }
    }

    for (const p of pwds) dfs(p, new Set([p]));

    return ans;
}

4、复杂度

时间复杂度： $O(k*k^{2n})$
空间复杂度： $O(k*k^{2n})$

5、执行结果

6、思路2

这是思路1的优化版，时间复杂度更低。主要是猜测以任意密码开头都有可能找到最短字符串，因此枚举时只取第一个密码作为起点构造字符串。代码的不同表现在倒数第二行，移除了遍历，只取第一个密码 pwds[0] 进行回溯。

7、代码

function crackSafe(n: number, k: number): string {
    if (k === 1) return '0'.padStart(n, '0');

    // 生成pwds
    const pwds = new Array(k ** n).fill('0').map((v, i) => {
        return k < 2 ? v : i.toString(k).padStart(n, "0");
    });

    if (n === 1) return pwds.join('');

    const pwdMap = new Map();
    for (const p of pwds) {
        const prefix = p.slice(0, n - 1);
        if (!pwdMap.has(prefix)) pwdMap.set(prefix, []);
        pwdMap.get(prefix).push(p);
    }

    // 组合pwds
    let ans = '';
    function dfs(cur: string, used: Set<string>) {
        if (ans) return;
        if (used.size === pwds.length) {
            const nums = [...used];
            ans = nums[0] + nums.slice(1).map(w => w.slice(-1)).join('');
            return;
        }

        const nums = pwdMap.get(cur.slice(1));
        for (const n of nums) {
            if (used.has(n)) continue;
            used.add(n);
            dfs(n, used);
            used.delete(n);
        }
    }

    dfs(pwds[0], new Set([pwds[0]]));

    return ans;
}

8、复杂度

时间复杂度： $O(k*k^n)$
空间复杂度： $O(k*k^n)$

9、执行结果

1、题干

给你一个数组 pairs ，其中 pairs[i] = [x_i, y_i] ，并且满足：

pairs 中没有重复元素
x_i < y_i

令 ways 为满足下面条件的有根树的方案数：

树所包含的所有节点值都在 pairs 中。
一个数对 [x_i, y_i] 出现在 pairs 中 当且仅当 x_i 是 y_i 的祖先或者 y_i 是 x_i的祖先。
注意：构造出来的树不一定是二叉树。

两棵树被视为不同的方案当存在至少一个节点在两棵树中有不同的父节点。

请你返回：

如果 ways == 0 ，返回 0 。
如果 ways == 1 ，返回 1 。
如果 ways > 1 ，返回 2 。

一棵 有根树 指的是只有一个根节点的树，所有边都是从根往外的方向。

我们称从根到一个节点路径上的任意一个节点（除去节点本身）都是该节点的祖先。根节点没有祖先。

示例 1：

输入：pairs = [[1,2],[2,3]]
输出：1
解释：如上图所示，有且只有一个符合规定的有根树。

示例 2：

输入：pairs = [[1,2],[2,3],[1,3]]
输出：2
解释：有多个符合规定的有根树，其中三个如上图所示。

示例 3：

输入：pairs = [[1,2],[2,3],[2,4],[1,5]]
输出：0
解释：没有符合规定的有根树。

提示：

1 <= pairs.length <= 10⁵
1 <= x_i< y_i <= 500
pairs 中的元素互不相同。

尽力了，磨了大半天，只想出这么个方法。思路还算清晰，但无法证明解法的正确性，能AC纯粹靠运气。。。

2、解题思路

先排除 ways = 0 不存在根节点的情况
再排除 ways = 0 存在互为祖先节点的情况
- 如果任意两个节点 a 和 b 不存在祖孙关系，但二者祖孙链上有共同的节点 c，则 c 是 a 和 b 的共同祖先
- 若后续能推出 a 或 b 是 c 的祖先，则说明存在矛盾无法构建树
再排除 ways = 2 的情况：节点存在祖孙关系，且祖孙链长度相同
- 补充：任意父节点只有1个子节点都会造成这种情况，此时父子节点可以互换位置构成多棵树
剩余情况 ways = 1
- 补充：所有父节点都有2个以上子节点才能保证唯一

3、代码

var checkWays = function (pairs) {
    const linkDict = [];
    const add = (i, j) => {
        if (!linkDict[i]) linkDict[i] = new Set();
        linkDict[i].add(j);
    };
    for (const [i, j] of pairs) add(i, j), add(j, i);
    const keys = linkDict.map((v, i) => i).filter((v) => v > -1);
    keys.sort((a, b) => linkDict[b].size - linkDict[a].size);

    // 排除 ways = 0: 不存在根节点
    if (linkDict[keys[0]].size !== keys.length - 1) return 0;

    // 排除 ways = 0: 存在互为祖先的节点
    const ancestorDict = keys.reduce((a, c) => (a[c] = new Set(), a), []);
    for (let i = 1; i < keys.length; i++) {
        for (let j = i + 1; j < keys.length; j++) {
            if (linkDict[keys[i]].has(keys[j])) continue;
            for (const li of linkDict[keys[i]]) {
                if (li === keys[0] || !linkDict[keys[j]].has(li)) continue;
                if (ancestorDict[keys[i]].has(li) || ancestorDict[keys[j]].has(li)) return 0;
                ancestorDict[li].add(keys[i]), ancestorDict[li].add(keys[j]);
            }
        }
    }

    // 排除 ways = 2: 节点存在祖孙关系，且祖孙链长度相同
    for (const [i, j] of pairs) if (linkDict[i].size === linkDict[j].size) return 2;

    return 1;
};

4、复杂度

时间复杂度： $O(n^3)$ ，其中 $n$ 为节点数
空间复杂度： $O(n^2)$

5、执行结果

1、题干

树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [a_i, b_i] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

示例 1：

输入: edges = [[1,2],[1,3],[2,3]]
输出: [2,3]

示例 2：

输入: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
输出: [1,4]

提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

注意：本题与主站 684 题相同： https://leetcode-cn.com/problems/redundant-connection/

并查集还没学会，只能先用树和图的思想解题

2、解题思路

在树的概念中，叶子结点是指没有子结点的结点，叶子节点只跟父节点存在关联，即只有1条边。如果某个节点下只有叶子节点，把该节点下的所有叶子节点都移除掉之后它自己就变成了叶子节点。如果循环往复地移除树的所有叶子节点，最终这棵树的节点数会变为0 。

如果按题目意思在树中添加一条边，这棵树会变成一个有环图，而在移除所有叶子节点的操作中，环上的所有节点都不会被移除，本题就是利用这个结论解题。

总体思路 ：循环往复地移除树上所有的叶子节点，直到不存在叶子节点，最后遍历找到环中最后出现的边。

大体步骤 ：

先用矩阵建立节点关联关系，记为 matrix
- matrix 是一维数组，下标表示节点值
- matrix 中的元素是哈希集合，集合中包含与当前节点关联的所有节点
遍历 matrix 并把当前节点加入队列 queue 中，进行叶子节点的判断与移除
- 若该节点是叶子节点，则双向移除该节点与父节点的关联关系，同时把父节点加入队列 queue 中进行下一轮处理
- 若该节点不是叶子节点则跳过
最后遍历二维数组 edges 并在 matrix 中查找出处于环上且序号最大的边

3、代码

var findRedundantConnection = function (edges) {
    const n = edges.length, matrix = new Array(n + 1).fill(0);

    for (const [i, j] of edges) {
        !matrix[i] ? (matrix[i] = new Set([j])) : matrix[i].add(j);
        !matrix[j] ? (matrix[j] = new Set([i])) : matrix[j].add(i);
    }

    for (let k = 1; k <= n; k++) {
        const queue = [k];

        for (const i of queue) {
            if (matrix[i].size !== 1) continue;

            const j = matrix[i].keys().next().value;
            matrix[i].delete(j), matrix[j].delete(i);
            queue.push(j);
        }
    }

    return edges.reduce((a, [i, j]) => (matrix[i].size > 1 && matrix[j].size > 1 ? [i, j] : a), null);
};

4、复杂度

时间复杂度： $O(nlogn)$ ，复杂度比较高的代码在双层循环剪叶子那一段，外层循环 $n$ 次，内层循环最多为树的高度 $logn$ 次
空间复杂度： $O(n)$

5、执行结果

执行用时: 68 ms
内存消耗: 42.1 MB

1、题干

树可以看成是一个连通且无环的无向图。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

示例 1：

输入: edges = [[1,2],[1,3],[2,3]]
输出: [2,3]

示例 2：

输入: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
输出: [1,4]

提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

注意：本题与主站 684 题相同： https://leetcode-cn.com/problems/redundant-connection/

并查集还没学会，只能先用树和图的思想解题

2、解题思路

总体思路 ：循环往复地移除树上所有的叶子节点，直到不存在叶子节点，最后遍历找到环中最后出现的边。

大体步骤 ：

先用矩阵建立节点关联关系，记为 matrix
- matrix 是一维数组，下标表示节点值
- matrix 中的元素是哈希集合，集合中包含与当前节点关联的所有节点
遍历 matrix 并把当前节点加入队列 queue 中，进行叶子节点的判断与移除
- 若该节点是叶子节点，则双向移除该节点与父节点的关联关系，同时把父节点加入队列 queue 中进行下一轮处理
- 若该节点不是叶子节点则跳过
最后遍历二维数组 edges 并在 matrix 中查找出处于环上且序号最大的边

3、代码

var findRedundantConnection = function (edges) {
    const n = edges.length, matrix = new Array(n + 1).fill(0);

    for (const [i, j] of edges) {
        !matrix[i] ? (matrix[i] = new Set([j])) : matrix[i].add(j);
        !matrix[j] ? (matrix[j] = new Set([i])) : matrix[j].add(i);
    }

    for (let k = 1; k <= n; k++) {
        const queue = [k];

        for (const i of queue) {
            if (matrix[i].size !== 1) continue;

            const j = matrix[i].keys().next().value;
            matrix[i].delete(j), matrix[j].delete(i);
            queue.push(j);
        }
    }

    return edges.reduce((a, [i, j]) => (matrix[i].size > 1 && matrix[j].size > 1 ? [i, j] : a), null);
};

4、复杂度

时间复杂度： $O(nlogn)$ ，复杂度比较高的代码在双层循环剪叶子那一段，外层循环 $n$ 次，内层循环最多为树的高度 $logn$ 次
空间复杂度： $O(n)$

5、执行结果

执行用时: 68 ms
内存消耗: 42.1 MB

1、题干

城市用一个 双向连通 图表示，图中有 n 个节点，从 1 到 n 编号（包含 1 和 n）。图中的边用一个二维整数数组 edges 表示，其中每个 edges[i] = [u_i, v_i] 表示一条节点 u_i 和节点 v_i 之间的双向连通边。每组节点对由 最多一条 边连通，顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。

每个节点都有一个交通信号灯，每 change 分钟改变一次，从绿色变成红色，再由红色变成绿色，循环往复。所有信号灯都同时改变。你可以在 任何时候 进入某个节点，但是只能在节点 信号灯是绿色时 才能离开。如果信号灯是绿色，你不能在节点等待，必须离开。

第二小的值 是 严格大于 最小值的所有值中最小的值。

例如，[2, 3, 4] 中第二小的值是 3 ，而 [2, 2, 4] 中第二小的值是 4 。

给你 n、edges、time 和 change ，返回从节点 1 到节点 n 需要的 第二短时间 。

注意：

你可以 任意次 穿过任意顶点，包括 1 和 n 。
你可以假设在 启程时 ，所有信号灯刚刚变成绿色。

示例 1：

输入：n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出：13
解释：
上面的左图展现了给出的城市交通图。
右图中的蓝色路径是最短时间路径。
花费的时间是：
- 从节点 1 开始，总花费时间=0
- 1 -> 4：3 分钟，总花费时间=3
- 4 -> 5：3 分钟，总花费时间=6
因此需要的最小时间是 6 分钟。

右图中的红色路径是第二短时间路径。
- 从节点 1 开始，总花费时间=0
- 1 -> 3：3 分钟，总花费时间=3
- 3 -> 4：3 分钟，总花费时间=6
- 在节点 4 等待 4 分钟，总花费时间=10
- 4 -> 5：3 分钟，总花费时间=13
因此第二短时间是 13 分钟。

示例 2：

输入：n = 2, edges = [[1,2]], time = 3, change = 2
输出：11
解释：
最短时间路径是 1 -> 2 ，总花费时间 = 3 分钟
第二短时间路径是 1 -> 2 -> 1 -> 2 ，总花费时间 = 11 分钟

提示：

2 <= n <= 10⁴
n - 1 <= edges.length <= min(2 * 10⁴, n * (n - 1) / 2)
edges[i].length == 2
1 <= u_i, v_i <= n
u_i != v_i
不含重复边
每个节点都可以从其他节点直接或者间接到达
1 <= time, change <= 10³

2、解题思路

将路径数组 edges 转为邻接矩阵便于后续搜索
- 转换过程中注意本题是双向连通图，任意边上的两个点都可以作为出发点
利用BFS求最短路径步数 min1 和次短路径步数 min2，BFS过程中需要注意剪枝：
- 剪枝1：若 min2 已经找到则退出
- 剪枝2：若从当前节点到达下一节点的步数 step+1 与到达下一节点的最小步数 minSteps.get(k) 之差不小于2 step + 1 - minSteps.get(k) >= 2，则跳过
- 剪枝3：同一层级每个节点只出现一次
按最短路径逐步叠加通过时间和等待红灯时间

这里剪枝的主要方式跟大多数题解不太一样，大部分题解都是利用节点不可能访问超过2次作为主要剪枝方式，确实没有想到这个点；这里主要利用次短路径与最短路径步数差值不超过2进行剪枝，原因是最短路径在任意节点上重复一个来回只需要2步，若次短路径的步数比最短路径多2步以上则说明其不能成为次短。

3、代码

var secondMinimum = function (n, edges, time, change) {
    edges = edges.reduce((a, c) => {
        // 双向连通图，建表时两个都可以作为出发点
        !a[c[0]] ? (a[c[0]] = [c[1]]) : a[c[0]].push(c[1]);
        !a[c[1]] ? (a[c[1]] = [c[0]]) : a[c[1]].push(c[0]);
        return a;
    }, new Array(n + 1));

    let min1 = Infinity, min2 = Infinity, nodes = new Set([1]), step = 1;
    const minSteps = new Map();

    while (nodes.size && min2 === Infinity) {
        const nextNodes = new Set();
        for (const i of nodes) {
            minSteps.set(i, step);
            if (i === n) min1 === Infinity || min1 === step ? (min1 = step) : (min2 = step);
            for (const k of edges[i]) {
                if (minSteps.has(k) && step + 1 - minSteps.get(k) >= 2) continue;
                nextNodes.add(k);
            }
        }

        step++;
        nodes = nextNodes;
    }

    let cost = 0;
    for (let i = 1; i < Math.min(min1 + 2, min2); i++) {
        if (((cost / change) >> 0) % 2) cost += change - (cost % change);
        cost += time;
    }

    return cost;
};

4、执行结果

执行用时: 400 ms
内存消耗: 66.9 MB

207.课程表

2021年12月13日 · 阅读需 5 分钟

Whilconn

1、题干

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [a_i, b_i] ，表示如果要学习课程 a_i 则必须先学习课程 b_i。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

1 <= numCourses <= 2000
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= a_i, b_i < numCourses
prerequisites[i] 中的所有课程对 互不相同

2、解题思路

题干很长，浓缩下就简单很多：给一个有向图，判定其中是否有环 。总的思路是 BFS 或 DFS 遍历整个图，如果存在环则返回 false，否则返回 true。

第一步 ：把先修课程 prerequisites 转换为二维数组，即用二维数组存储图的信息
- 创建二维数组 edges 来表示先修课程，下标表示课程，内层数组表示先修课程集合
- edges[i] 中的下标 i 表示课程 i ，edges[i] 表示课程i的先修课程集合
- edges[i][j] 表示课程 i 的一个先修课程，edges[i][j] 的值是 edges 的一个下标

第二步 ：按课程序号从0开始深度遍历edges，判定图中是否存在环

第三步 ：以任意课程 c 为起始点深度遍历其先修课程，过程中注意3点：
- 所有遍历过的节点使用哈希集合 visited 记录，以达到剪枝效果避免超时
- 当前路径遍历过的节点使用哈希集合 paths 记录，如果当前节点已存在于 paths 中，说明存在环
- 如果课程 c2 后续路径合法，记得将其从 paths 中移除，以免干扰其他路径遍历（类似回溯中的状态重置）

3、复杂度

时间复杂度: $O(n)$
空间复杂度: $O(n)$

4、代码

var canFinish = function (numCourses, prerequisites) {
    // 1、把先修课程`prerequisites`转换为二维数组表示的图
    const edges = new Array(numCourses).fill(0).map(() => []);
    for (let p of prerequisites) edges[p[1]].push(p[0]);

    // 以课程c为起始点，深度遍历所有先修课程
    const visited = new Set();
    function dfs(c, paths) {
        if (visited.has(c)) return false;
        visited.add(c);

        paths.add(c);
        for (const c2 of edges[c]) {
            if (paths.has(c2) || dfs(c2, paths)) return true;
            paths.delete(c2);
        }

        return false;
    }

    // 2、按课程序号从0开始深度遍历`edges`，判定图中是否存在环
    for (let i = 0; i < edges.length; i++) {
        if (dfs(i, new Set())) return false;
    }

    return true;
};

1、题干​

2、思路​

3、代码​

4、复杂度​

5、执行结果​

1、题干​

2、思路​

3、代码​

4、复杂度​

5、执行结果​

1、题干​

2、思路1​

3、代码​

4、复杂度​

5、执行结果​

6、思路2​

7、代码​

8、复杂度​

9、执行结果​

1、题干​

2、解题思路​

3、代码​

4、复杂度​

5、执行结果​

1、题干​

2、解题思路​

3、代码​

4、复杂度​

5、执行结果​

1、题干​

2、解题思路​

3、代码​

4、复杂度​

5、执行结果​

1、题干​

2、解题思路​

3、代码​

4、执行结果​

1、题干​

2、解题思路​

3、复杂度​

4、代码​

1、题干

2、思路

3、代码

4、复杂度

5、执行结果

1、题干

2、思路

3、代码

4、复杂度

5、执行结果

1、题干

2、思路1

3、代码

4、复杂度

5、执行结果

6、思路2

7、代码

8、复杂度

9、执行结果

1、题干

2、解题思路

3、代码

4、复杂度

5、执行结果

1、题干

2、解题思路

3、代码

4、复杂度

5、执行结果

1、题干

2、解题思路

3、代码

4、复杂度

5、执行结果

1、题干

2、解题思路

3、代码

4、执行结果

1、题干

2、解题思路

3、复杂度

4、代码