1、题干
给你一个下标从 0 开始的整数数组 arr 和一个 m x n 的整数 矩阵 mat 。arr 和 mat 都包含范围 [1,m * n] 内的 所有 整数。
从下标 0 开始遍历 arr 中的每个下标 i ,并将包含整数 arr[i] 的 mat 单元格涂色。
请你找出 arr 中第一个使得 mat 的某一行或某一列都被涂色的元素,并返回其下标 i 。
示例 1:
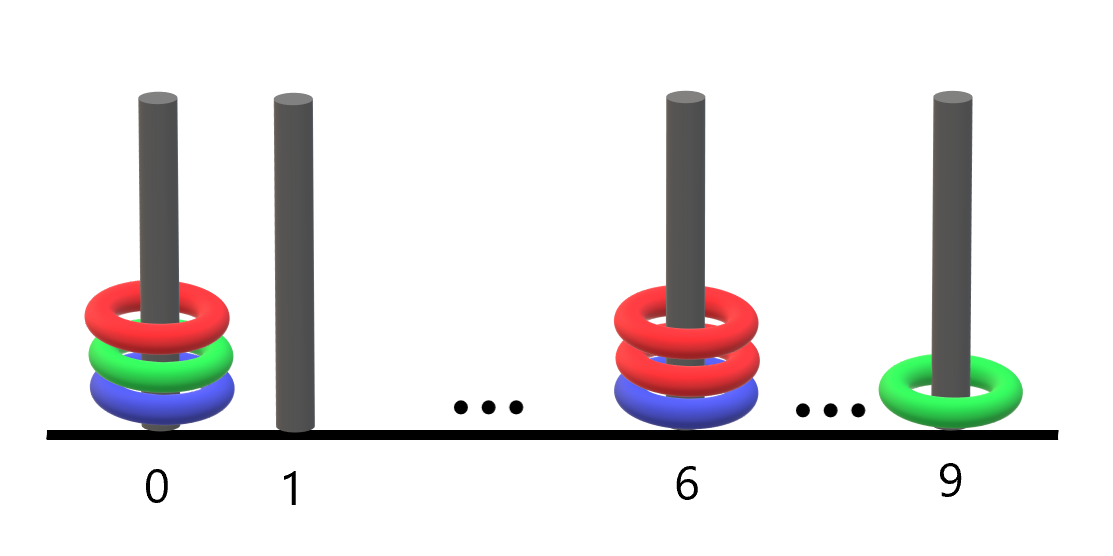
输入:arr = [1,3,4,2], mat = [[1,4],[2,3]]
输出:2
解释:遍历如上图所示,arr[2] 在矩阵中的第一行或第二列上都被涂色。
示例 2:
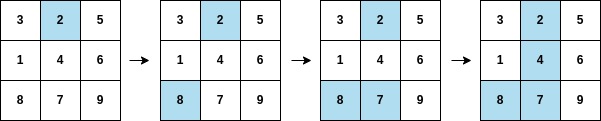
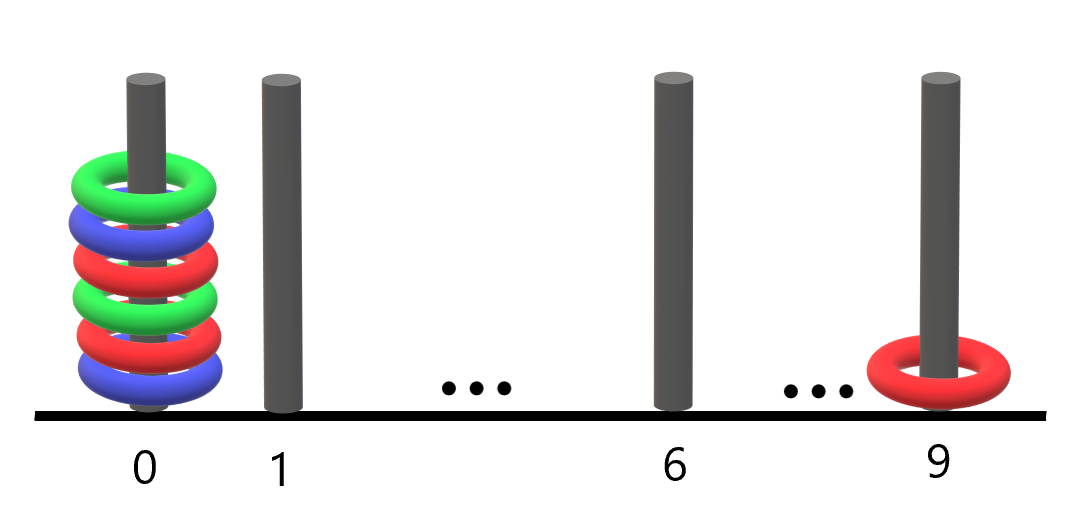
输入:arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
输出:3
解释:遍历如上图所示,arr[3] 在矩阵中的第二列上都被涂色。
提示:
m == mat.lengthn = mat[i].lengtharr.length == m * n1 <= m, n <= 1051 <= m * n <= 1051 <= arr[i], mat[r][c] <= m * narr中的所有整数 互不相同mat中的所有整数 互不相同
2、思路
模拟题,对行列涂色计数即可
3、代码
function firstCompleteIndex(arr: number[], mat: number[][]): number {
const map = new Array(arr.length + 1);
for (let i = 0; i < mat.length; i++) {
for (let j = 0; j < mat[i].length; j++) {
map[mat[i][j]] = [i, j];
}
}
const rows = new Array(mat.length).fill(0), cols = new Array(mat[0].length).fill(0);
for (let i = 0; i < arr.length; i++) {
const [r, c] = map[arr[i]];
rows[r]++, cols[c]++;
if (rows[r] === mat[0].length || cols[c] === mat.length) return i;
}
return -1;
};