1、题干
给定一个二叉搜索树,请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1:
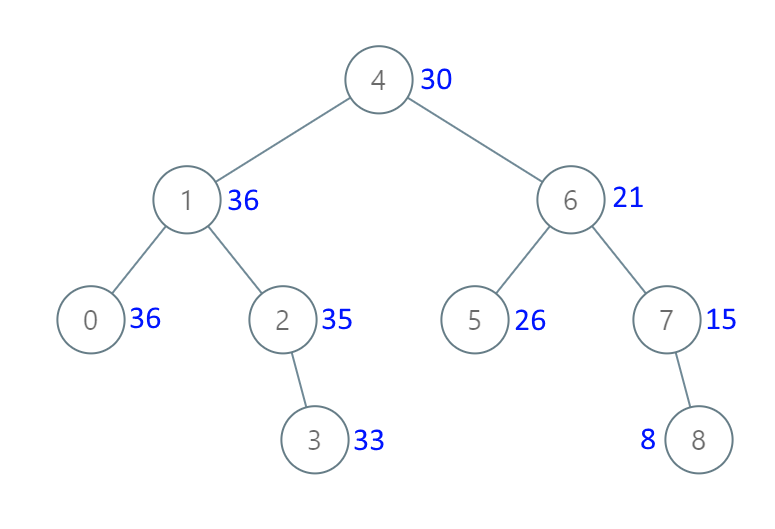
输入:root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
注意:
- 本题与主站 538 题相同: https://leetcode-cn.com/problems/convert-bst-to-greater-tree/
- 本题与主站 1038 题相同:https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/
2、解题思路
按中序相反的顺序(右子节点、父节点、左子节点)深度遍历所有节点,所有节点将会从大到小依次被访问,遍历过程中利用前缀和思想叠加节点之和,将当前节点值修改为前缀和加自身值presum + node.val即可。
如果不好理解,可以使用中序遍历所有节点并将节点依次存入数组,这样数组中的节点是按照值的大小升序排列,然后再倒序遍历数组并累加节点值、修改节点值即可。
3、代码
var convertBST = function (root) {
let presum = 0;
function dfs(node) {
if (!node) return;
dfs(node.right);
node.val = (presum += node.val);
dfs(node.left, node.val);
}
return dfs(root), root;
};
4、复杂度
时间复杂度:
空间复杂度:
5、执行结果