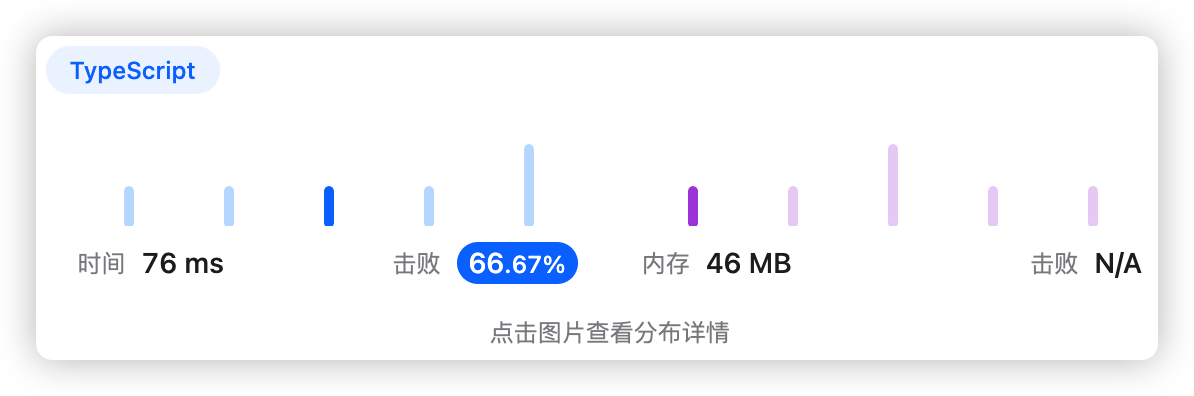
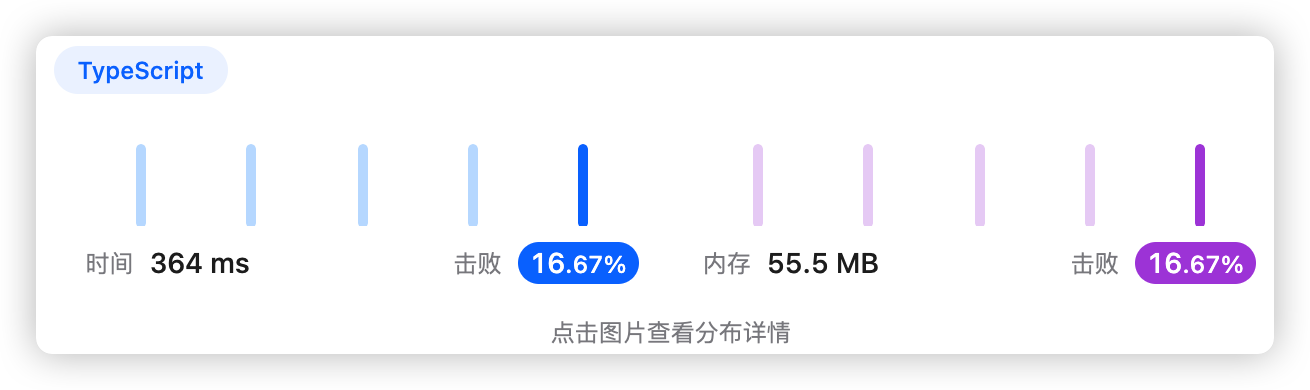
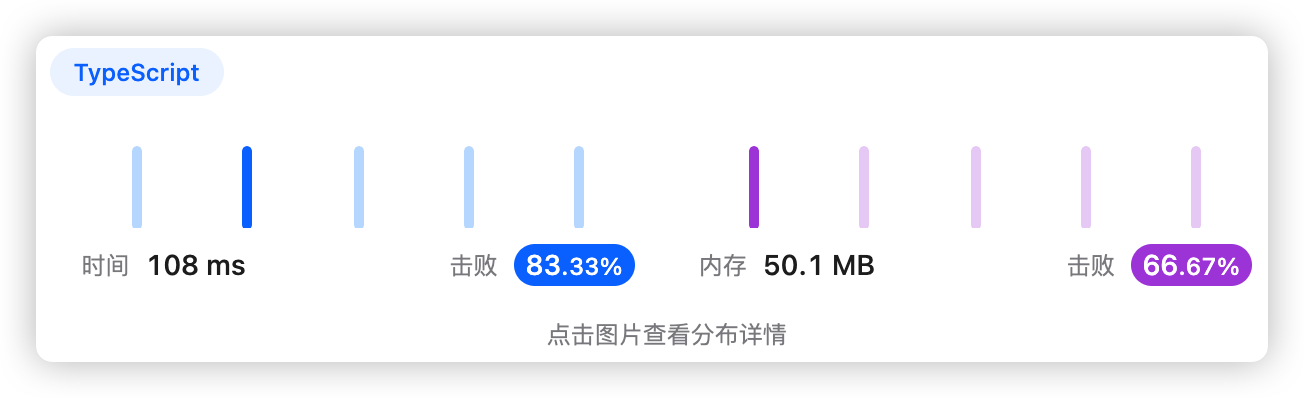
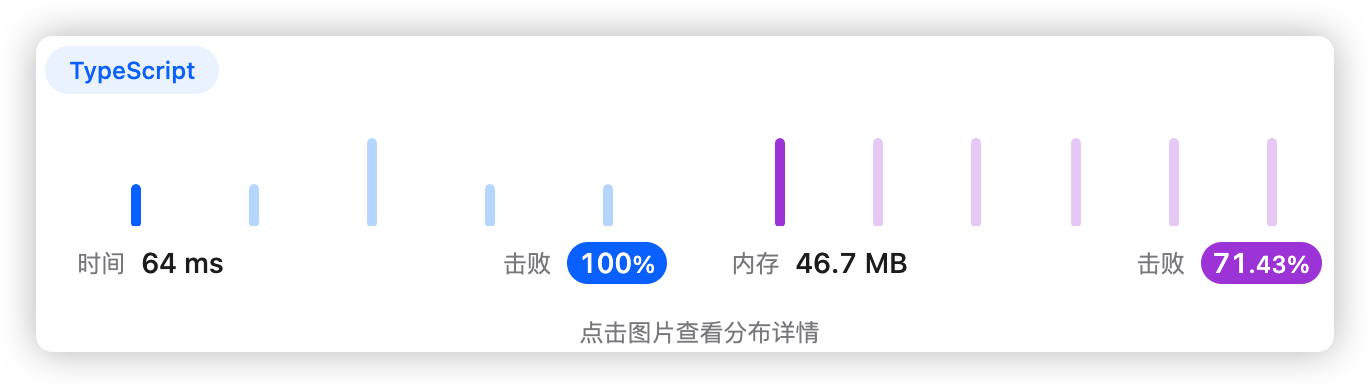
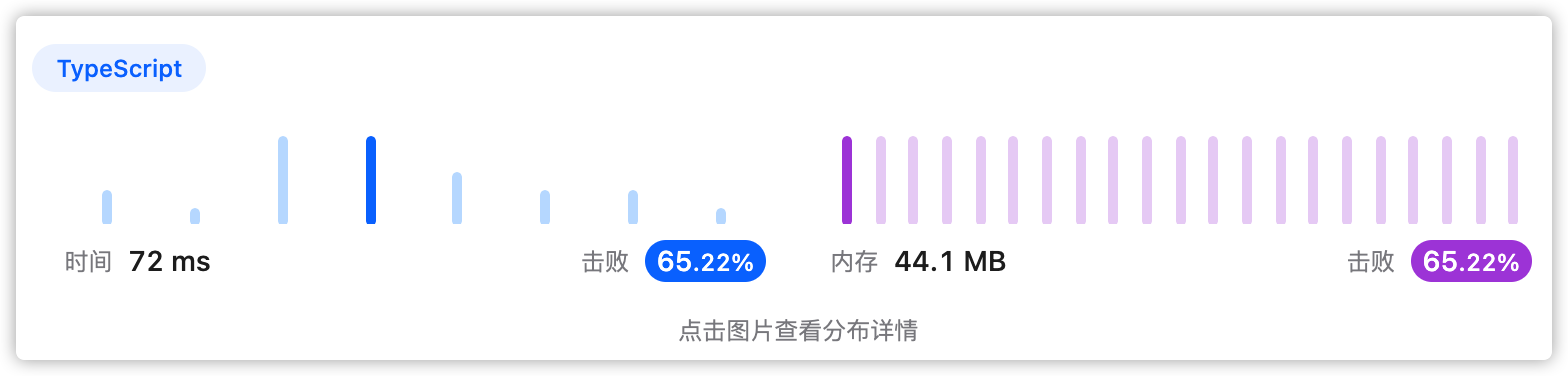
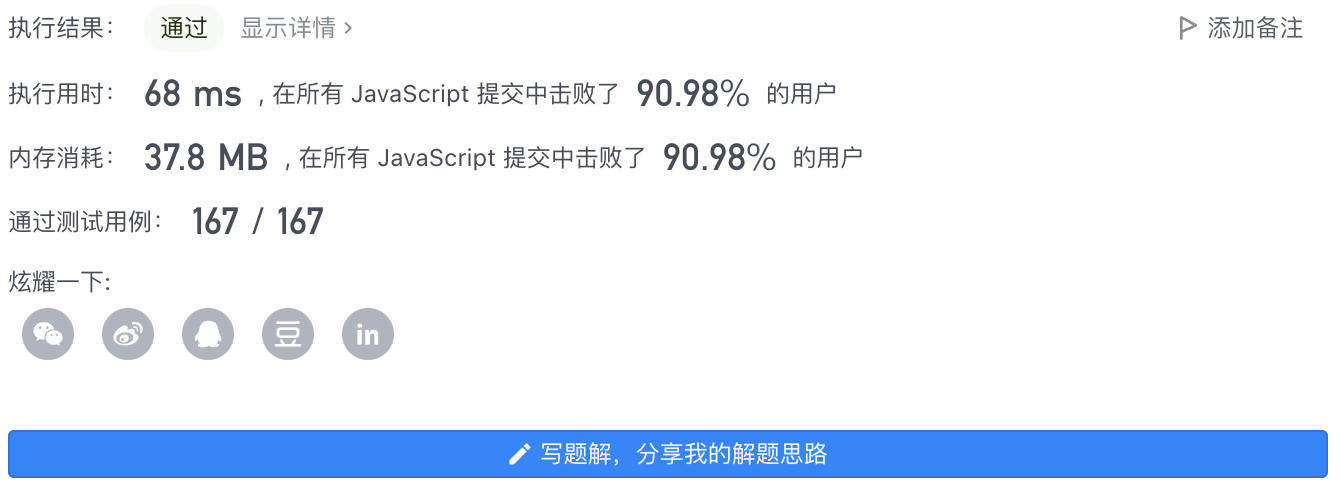
1、题干​

给你一个下标从 0 开始的整数数组 nums ，如果满足下述条件，则认为数组 nums 是一个 美丽数组 ：

• nums.length 为偶数
• 对所有满足 i % 2 == 0 的下标 i ，nums[i] != nums[i + 1] 均成立

注意，空数组同样认为是美丽数组。

你可以从 nums 中删除任意数量的元素。当你删除一个元素时，被删除元素右侧的所有元素将会向左移动一个单位以填补空缺，而左侧的元素将会保持 不变 。

返回使 nums 变为美丽数组所需删除的 最少 元素数目。

示例 1：

输入：nums = [1,1,2,3,5]
输出：1
解释：可以删除 nums[0] 或 nums[1] ，这样得到的 nums = [1,2,3,5] 是一个美丽数组。可以证明，要想使 nums 变为美丽数组，至少需要删除 1 个元素。

示例 2：

输入：nums = [1,1,2,2,3,3]
输出：2
解释：可以删除 nums[0] 和 nums[5] ，这样得到的 nums = [1,2,2,3] 是一个美丽数组。可以证明，要想使 nums 变为美丽数组，至少需要删除 2 个元素。

提示：

• 1 <= nums.length <= 105
• 0 <= nums[i] <= 105

2、思路​

模拟一遍删除过程就能过。其他题解说是贪心，也有证明过程，看完还是不懂不理解。这题证明比AC难得多。

3、代码​

function minDeletion(nums: number[]): number {
    let cur = -Infinity, size = 0;
    
    for (const k of nums) {
        if (size % 2 === 0 || k !== cur) cur = k, size++;
    }

    return nums.length - size + (size % 2);
};

1、题干​

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 3：

输入：s = "(]"
输出：false

提示：

• 1 <= s.length <= 104
• s 仅由括号 '()[]{}' 组成

2、思路​

遍历字符串，使用栈存储字符，若栈顶字符与当前字符配对则出栈，否则入栈，最后栈为空则字符串有效

3、代码​

function isValid(s: string): boolean {
    const stack = [], map = { "(": ")", "[": "]", "{": "}" };
    for (const c of s) {
        map[stack.at(-1)] === c ? stack.pop() : stack.push(c);
    }
    return !stack.length;
};

1、题干​

如果你熟悉 Shell 编程，那么一定了解过花括号展开，它可以用来生成任意字符串。

花括号展开的表达式可以看作一个由 花括号、逗号 和 小写英文字母 组成的字符串，定义下面几条语法规则：

• 如果只给出单一的元素 x，那么表达式表示的字符串就只有 "x"。R(x) = {x}
  • 例如，表达式 "a" 表示字符串 "a"。
  • 而表达式 "w" 就表示字符串 "w"。
• 当两个或多个表达式并列，以逗号分隔，我们取这些表达式中元素的并集。R({e_1,e_2,...}) = R(e_1) ∪ R(e_2) ∪ ...
  • 例如，表达式 "{a,b,c}" 表示字符串 "a","b","c"。
  • 而表达式 "{{a,b},{b,c}}" 也可以表示字符串 "a","b","c"。
• 要是两个或多个表达式相接，中间没有隔开时，我们从这些表达式中各取一个元素依次连接形成字符串。R(e_1 + e_2) = {a + b for (a, b) in R(e_1) × R(e_2)}
  • 例如，表达式 "{a,b}{c,d}" 表示字符串 "ac","ad","bc","bd"。
• 表达式之间允许嵌套，单一元素与表达式的连接也是允许的。
  • 例如，表达式 "a{b,c,d}" 表示字符串 "ab","ac","ad"​​​​​​。
  • 例如，表达式 "a{b,c}{d,e}f{g,h}" 可以表示字符串 "abdfg", "abdfh", "abefg", "abefh", "acdfg", "acdfh", "acefg", "acefh"。

给出表示基于给定语法规则的表达式 expression，返回它所表示的所有字符串组成的有序列表。

假如你希望以「集合」的概念了解此题，也可以通过点击 “显示英文描述” 获取详情。

示例 1：

输入：expression = "{a,b}{c,{d,e}}"
输出：["ac","ad","ae","bc","bd","be"]

示例 2：

输入：expression = "{{a,z},a{b,c},{ab,z}}"
输出：["a","ab","ac","z"]
解释：输出中 不应 出现重复的组合结果。

提示：

• 1 <= expression.length <= 60
• expression[i] 由 '{'，'}'，',' 或小写英文字母组成
• 给出的表达式 expression 用以表示一组基于题目描述中语法构造的字符串

2、思路​

本题要处理的子表达式主要包括3类：

• 单层：{xxx,xxx}
• 嵌套：{{xxx},{xxx}}
• 相接：{xxx}{xxx}，xxx{xxx}，{xxx}xxx

具体代码实现逻辑如下：

• 扁平化：把最内层的单层表达式提取到上一层（这会逐渐把嵌套和单层表达式都处理掉）
• 拼接组合：拼接组合最内层相接子表达式
• 重复这两个步骤直到表达式中没有任何花括号
• 最后对表达式进行拆分、去重、排序

3、代码​

function braceExpansionII(exp: string): string[] {
    const reg0 = /\{([a-z,]+)\}/g;
    const reg1 = new RegExp(`(?<![a-z}])${reg0.source}(?![a-z{])`, 'g');
    const reg2 = new RegExp(`(${reg0.source}){2,}|[a-z]+(${reg0.source})+|(${reg0.source})+[a-z]+`, 'g');

    while (1) {
        const f1 = reg1.test(exp);
        if (f1) exp = exp.replace(reg1, '$1');

        const f2 = reg2.test(exp);
        if (f2) {
            exp = exp.replace(reg2, (m) => {
                const reg = new RegExp(`${reg0.source}|[a-z]+`, 'g');

                const tokenGroup = (m.match(reg) || []).map(s => s.split(/,|\{|\}/).filter(Boolean));

                let ans = tokenGroup[0];
                for (let i = 1; i < tokenGroup.length; i++) {
                    const newAns = [];
                    for (const h of ans) {
                        for (const t of tokenGroup[i]) {
                            newAns.push(h + t);
                        }
                    }
                    ans = newAns;
                }

                return `{${ans.join(',')}}`
            });
        }

        if (!f1 && !f2) break;
    }

    return [...new Set(exp.split(','))].sort();
};

4、执行结果​

1、题干​

给你一个字符串 s ，它仅包含字符 'a' 和 'b'​​​​ 。

你可以删除 s 中任意数目的字符，使得 s 平衡 。当不存在下标对 (i,j) 满足 i < j ，且 s[i] = 'b' 的同时 s[j]= 'a' ，此时认为 s 是 平衡 的。

请你返回使 s 平衡 的 最少 删除次数。

示例 1：

输入：s = "aababbab"
输出：2
解释：你可以选择以下任意一种方案：
下标从 0 开始，删除第 2 和第 6 个字符（"aababbab" -> "aaabbb"），
下标从 0 开始，删除第 3 和第 6 个字符（"aababbab" -> "aabbbb"）。

示例 2：

输入：s = "bbaaaaabb"
输出：2
解释：唯一的最优解是删除最前面两个字符。

提示：

• 1 <= s.length <= 105
• s[i] 要么是 'a' 要么是 'b'​ 。​

本题跟剑指 Offer II 092. 翻转字符的思路一样

2、思路1​

循环剔除所有 ba 子串并累加剔除次数

3、代码​

function minimumDeletions(s: string): number {
    let ans = 0;
    while (s.includes('ba')) s = s.replace(/ba/g, () => (ans++, ''));
    return ans;
};

4、执行结果​

5、思路2​

思路1实际上是消除所有字符 b 后面的字符 a，可以使用常规遍历模拟消除过程。

具体实现时需要遍历字符串 s 两次，先统计字符 a 的个数，再消除字符 a。

6、代码​

function minimumDeletions(s: string): number {
    let ac = 0;
    for (let i = 0; i < s.length; i++) {
        if (s[i] === 'a') ac++;
    };

    let ans = 0, bc = 0;
    for (let i = 0; ac > 0 && i < s.length; i++) {
        if (s[i] === 'a') bc > 0 ? bc-- : ac--;
        else ans++, bc++, ac--;
    }

    return ans;
};

7、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

8、执行结果​

1、题干​

给你一份工作时间表 hours，上面记录着某一位员工每天的工作小时数。

我们认为当员工一天中的工作小时数大于 8 小时的时候，那么这一天就是「劳累的一天」。

所谓「表现良好的时间段」，意味在这段时间内，「劳累的天数」是严格 大于「不劳累的天数」。

请你返回「表现良好时间段」的最大长度。

示例 1：

输入：hours = [9,9,6,0,6,6,9]
输出：3
解释：最长的表现良好时间段是 [9,9,6]。

示例 2：

输入：hours = [6,6,6]
输出：0

提示：

• 1 <= hours.length <= 104
• 0 <= hours[i] <= 16

2、思路-前缀和+哈希表​

• 计算 hours 的前缀和数组 sums，当 hours[i] 大于 8 时前缀和 +1 否则 -1
• 将 sums[i] 与 i 分别作为键值存入哈希表 map；为保证结果时段最大，仅当哈希表中不存在 sums[i] 时才存入该键值对
• 如果 sums[i] 大于 0，则区间 [0,i] 可能是最长时段
• 如果 sums[i] 小于等于 0，则区间 [map.get(sums[i] - 1),i) 也可能是最长时段
• 所有备选时段长度的最大值即所求的最长时段

这题的前缀和在整数范围上具有连续性，所以能用哈希表

3、代码​

function longestWPI(hours: number[]): number {
    const sums = hours.map(() => 0);
    const map = new Map();

    let ans = 0;
    for (let i = 0; i < hours.length; i++) {
        sums[i] = (sums[i - 1] || 0) + (hours[i] > 8 ? 1 : -1);
        if (sums[i] > 0) ans = Math.max(ans, i + 1);
        else {
            if (map.has(sums[i] - 1)) ans = Math.max(ans, i - map.get(sums[i] - 1));
        }

        if (!map.has(sums[i])) map.set(sums[i], i);
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

5、执行结果​

6、前缀和+栈​

这个思路是我能写出来的吗

function longestWPI(hours: number[]): number {
    const sums = hours.map(() => 0);
    const minStack = [0];

    let ans = 0;
    for (let i = 0; i < hours.length; i++) {
        sums[i] = (sums[i - 1] || 0) + (hours[i] > 8 ? 1 : -1);
        if (sums[i] > 0) ans = Math.max(ans, i + 1);
        if (sums[i] < sums[minStack.at(-1)]) minStack.push(i);
    }

    for (let i = hours.length - 1; i > -1; i--) {
        while (sums[minStack.at(-1)] < sums[i]) {
            const l = minStack.pop();
            ans = Math.max(ans, i - l);
        }
    }

    return ans;
};

1、题干​

布尔表达式 是计算结果不是 true 就是 false 的表达式。有效的表达式需遵循以下约定：

• 't'，运算结果为 true
• 'f'，运算结果为 false
• '!(subExpr)'，运算过程为对内部表达式 subExpr 进行 逻辑非（NOT）运算
• '&(subExpr1, subExpr2, ..., subExprn)'，运算过程为对 2 个或以上内部表达式 subExpr1, subExpr2, ..., subExprn 进行 逻辑与（AND）运算
• '|(subExpr1, subExpr2, ..., subExprn)'，运算过程为对 2 个或以上内部表达式 subExpr1, subExpr2, ..., subExprn 进行 逻辑或（OR）运算

给你一个以字符串形式表述的 布尔表达式 expression，返回该式的运算结果。

题目测试用例所给出的表达式均为有效的布尔表达式，遵循上述约定。

示例 1：

输入：expression = "&(|(f))"
输出：false
解释：
首先，计算 |(f) --> f ，表达式变为 "&(f)" 。
接着，计算 &(f) --> f ，表达式变为 "f" 。
最后，返回 false 。

示例 2：

输入：expression = "|(f,f,f,t)"
输出：true
解释：计算 (false OR false OR false OR true) ，结果为 true 。

示例 3：

输入：expression = "!(&(f,t))"
输出：true
解释：
首先，计算 &(f,t) --> (false AND true) --> false --> f ，表达式变为 "!(f)" 。
接着，计算 !(f) --> NOT false --> true ，返回 true 。

提示：

• 1 <= expression.length <= 2 * 104
• expression[i] 为 '('、')'、'&'、'|'、'!'、't'、'f' 和 ',' 之一

Problem: 1106. 解析布尔表达式

[TOC]

思路

使用正则不断提取最小表达式进行计算，再将该表达式替换为计算结果。其中最小表达式就是题干中给出的3种情况："!(expr)"，"&(expr1,expr2,...)"，"|(expr1,expr2,...)"

代码

function parseBoolExpr(exp: string): boolean {
    const T = "t", F = "f", reg = /.\([^()]+\)/g;
    while (reg.test(exp)) {
        exp = exp.replace(reg, (m) => {
            if (m[0] === "&") return m.includes(F) ? F : T;
            if (m[0] === "|") return m.includes(T) ? T : F;
            return m.includes(T) ? F : T;
        });
    }
    return exp.includes(T);
}

结果

1、题干​

给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。

由于答案可能很大，因此 返回答案模 10^9 + 7 。

示例 1：

输入：arr = [3,1,2,4]
输出：17
解释：
子数组为 [3]，[1]，[2]，[4]，[3,1]，[1,2]，[2,4]，[3,1,2]，[1,2,4]，[3,1,2,4]。 
最小值为 3，1，2，4，1，1，2，1，1，1，和为 17。

示例 2：

输入：arr = [11,81,94,43,3]
输出：444

提示：

• 1 <= arr.length <= 3 * 104
• 1 <= arr[i] <= 3 * 104

解题思路​

单调栈，写得有点费力

代码​

function sumSubarrayMins(arr: number[]): number {
  let res = 0;

  function dfs(c: number) {
    const n = arr[c];
    let [mins, preSum] = c < arr.length - 1 ? dfs(c + 1) : [[], 0];

    let count = 1;
    while (mins.at(-1)?.at(0) >= n) {
      const pair = mins.pop();
      count += pair[1];
      preSum -= pair[1] * pair[0];
    }

    mins.push([n, count]);
    preSum = (preSum + n * count) % (1e9 + 7);
    res = (res + preSum) % (1e9 + 7);

    return [mins, preSum];
  }

  dfs(0);

  return res;
}

1、题干​

你正在参加一个多角色游戏，每个角色都有两个主要属性：攻击 和 防御 。给你一个二维整数数组 properties ，其中 properties[i] = [attacki, defensei] 表示游戏中第 i 个角色的属性。

如果存在一个其他角色的攻击和防御等级 都严格高于 该角色的攻击和防御等级，则认为该角色为 弱角色 。更正式地，如果认为角色 i 弱于 存在的另一个角色 j ，那么 attackj > attacki 且 defensej > defensei 。

返回 弱角色 的数量。

示例 1：

输入：properties = [[5,5],[6,3],[3,6]]
输出：0
解释：不存在攻击和防御都严格高于其他角色的角色。

示例 2：

输入：properties = [[2,2],[3,3]]
输出：1
解释：第一个角色是弱角色，因为第二个角色的攻击和防御严格大于该角色。

示例 3：

输入：properties = [[1,5],[10,4],[4,3]]
输出：1
解释：第三个角色是弱角色，因为第二个角色的攻击和防御严格大于该角色。

提示：

• 2 <= properties.length <= 105
• properties[i].length == 2
• 1 <= attacki, defensei <= 105

没想到官解那么巧妙的解法，提供一个普通思路。。。

2、解法1​

方便起见将角色属性数组长度 properties.length 记为 $n$。

总体思路

• 先升序排序：对属性数组 properties 按攻击力升序排序
• 再查找强角色：假设攻击力没有相同值，对于任意角色 i 如果能在区间 $[i+1, n-1]$ 内找到一个防御力更大的角色 j，就说明 i 是一个弱角色
• 预统计区间内最大防御力，加速查找：问题是在区间 $[i+1, n-1]$ 内找一个比较大的值需要遍历，时间复杂度不允许，因此可以先统计区间内的最大值，在查找的时候直接使用最大值进行比较即可

大体步骤

• 先对属性数组 properties 按攻击力升序排序
• 创建数组 maxDefs 用于记录区间最大防御力，对于任意元素 maxDefs[i] 表示区间 $[i, n-1]$ 内的最大防御力
  • 这里需要倒序遍历 properties，对于任意索引 i，maxDefs[i] 取当前防御力 properties[i][1] 与后续区间最大防御力 maxDefs[i + 1] 中的最大值
  • 最后 maxDefs 会形成一个单调递减的数列
• 最后顺序遍历 properties ，对于任意角色属性 properties[i]，如果能在区间 $[i+1, n-1]$ 找到一个攻击力防御力都更大的角色属性 properties[j]，即 properties[i][0] < properties[j][0] && properties[i][1] < maxDefs[j]，则说明这是一个弱角色
  • 注意这里需要跳过攻击力相同的角色

3、代码​

var numberOfWeakCharacters = function (properties) {
    properties.sort((a, b) => a[0] - b[0]);

    const n = properties.length, maxDefs = new Array(n).fill(0);
    for (let i = n - 1; i > -1; i--) {
        maxDefs[i] = Math.max(maxDefs[i + 1] || 0, properties[i][1]);
    }

    let count = 0;
    for (let i = 0; i < n - 1; i++) {
        let j = i + 1;
        // 跳过攻击力相同的角色
        while (j < n && properties[i][0] === properties[j][0]) j++;
        if (properties[i][1] < maxDefs[j]) count++;
    }

    return count;
};

4、复杂度​

• 时间复杂度：$O(nlogn)$ 到 $O(n^2)$ 之间
• 空间复杂度：$O(n)$

5、执行结果​

• 执行用时: 344 ms，超97%
• 内存消耗: 75.2 MB，超7%

6、解法1-优化​

问题：跳过攻击力相同的角色是后置的，在查找过程中通过遍历的方式逐一跳过，这里增加了时间复杂度 优化：可以参考官解的排序方式：依然按攻击力升序排序，但是当攻击力相同时按防御力降序排序。这里很巧妙地规避了需要跳过攻击力相同角色的问题，因为攻击力相同时按防御力降序排序，意味着后续区间如果出现更大的防御力必定不属于攻击力相同的角色

7、代码​

var numberOfWeakCharacters = function (properties) {
    properties.sort((a, b) => a[0] === b[0] ? b[1] - a[1] : a[0] - b[0]);

    const n = properties.length, maxDefs = new Array(n).fill(0);
    for (let i = n - 1; i > -1; i--) {
        maxDefs[i] = Math.max(maxDefs[i + 1] || 0, properties[i][1]);
    }

    let count = 0;
    for (let i = 0; i < n - 1; i++) {
        if (properties[i][1] < maxDefs[i + 1]) count++;
    }

    return count;
};

8、复杂度​

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(n)$

9、执行结果​

• 执行用时: 336 ms，超97%
• 内存消耗: 74.8 MB，超7%

如果把优化后的代码调整为按攻击力降序排序或者按倒序遍历查找弱角色，就跟官解一样了，记录区间最大值不再需要数组，只需要一个变量，空间复杂度可以降到 $O(1)$，时间复杂度相同。

1、题干​

如果字符串满足以下条件之一，则可以称之为 有效括号字符串（valid parentheses string，可以简写为 VPS）：

• 字符串是一个空字符串 ""，或者是一个不为 "(" 或 ")" 的单字符。
• 字符串可以写为 AB（A 与 B 字符串连接），其中 A 和 B 都是 有效括号字符串 。
• 字符串可以写为 (A)，其中 A 是一个 有效括号字符串 。

类似地，可以定义任何有效括号字符串 S 的 嵌套深度 depth(S)：

• depth("") = 0
• depth(C) = 0，其中 C 是单个字符的字符串，且该字符不是 "(" 或者 ")"
• depth(A + B) = max(depth(A), depth(B))，其中 A 和 B 都是 有效括号字符串
• depth("(" + A + ")") = 1 + depth(A)，其中 A 是一个 有效括号字符串

例如：""、"()()"、"()(()())" 都是 有效括号字符串（嵌套深度分别为 0、1、2），而 ")(" 、"(()" 都不是 有效括号字符串 。

给你一个 有效括号字符串 s，返回该字符串的 s 嵌套深度 。

示例 1：

输入：s = "(1+(2*3)+((8)/4))+1"
输出：3
解释：数字 8 在嵌套的 3 层括号中。

示例 2：

输入：s = "(1)+((2))+(((3)))"
输出：3

提示：

• 1 <= s.length <= 100
• s 由数字 0-9 和字符 '+'、'-'、'*'、'/'、'('、')' 组成
• 题目数据保证括号表达式 s 是 有效的括号表达式

2、解题思路​

根据题意统计左括号数量sum和最大值max，遇到左括号(数量sum加1并更新最大值max，遇到右括号)数量sum减1，最后返回最大值max。

3、代码​

var maxDepth = function (s) {
    let sum = 0, max = 0;
    for (const c of s) {
        if (c === '(') max = Math.max(++sum, max);
        else if (c === ')') --sum;
    }
    return max;
};

4、执行结果​

执行用时: 72 ms 内存消耗: 39 MB

5、整活​

用数组的reduce函数遍历字符串，把代码缩减成1行，空间和时间也都有所减少，突然觉得自己又行了😏。

但是，实际项目不推荐这么写，一般情况下写代码更应该重视可维护性。试想这样一行代码过两天自己都看不懂，接手的人心理活动又会是什么样😂。

6、代码​

var maxDepth = s => [].reduce.call(s, (a, c) => (c === '(' ? ++a[0] > a[1] && (a[1] = a[0]) : c === ')' && --a[0], a), [0, 0])[1];

7、执行结果​

1、题干​

给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 '/' 开头），请你将其转化为更加简洁的规范路径。

在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点 （..） 表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠（即，'//'）都被视为单个斜杠 '/' 。 对于此问题，任何其他格式的点（例如，'...'）均被视为文件/目录名称。

请注意，返回的 规范路径 必须遵循下述格式：

• 始终以斜杠 '/' 开头。
• 两个目录名之间必须只有一个斜杠 '/' 。
• 最后一个目录名（如果存在）不能 以 '/' 结尾。
• 此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。

返回简化后得到的 规范路径 。

示例 1：

输入：path = "/home/"
输出："/home"
解释：注意，最后一个目录名后面没有斜杠。 

示例 2：

输入：path = "/../"
输出："/"
解释：从根目录向上一级是不可行的，因为根目录是你可以到达的最高级。

示例 3：

输入：path = "/home//foo/"
输出："/home/foo"
解释：在规范路径中，多个连续斜杠需要用一个斜杠替换。

示例 4：

输入：path = "/a/./b/../../c/"
输出："/c"

提示：

• 1 <= path.length <= 3000
• path 由英文字母，数字，'.'，'/' 或 '_' 组成。
• path 是一个有效的 Unix 风格绝对路径。

2、解法1​

将path字符串按/分割为目录数组dirs，过滤dirs中的空串和.号；再遍历dirs，遇到..则出栈，反之入栈；最后使用/拼接栈中剩余目录。

3、代码​

var simplifyPath = function (path) {
    const dirs = path.split('/').filter(c => c && c !== '.');
    return '/' + dirs.reduce((acc, cur) => (cur === '..' ? acc.pop() : acc.push(cur), acc), []).join('/');
};

4、执行结果​

5、解法2​

使用Node.js内置的path模块解析路径。

6、代码​

var simplifyPath = function (p) {
    return require('path').resolve(p);
};

7、执行结果​

执行用时: 84 ms 内存消耗: 39.9 MB