1、题干
城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由 最多一条 边连通,顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。
每个节点都有一个交通信号灯,每 change 分钟改变一次,从绿色变成红色,再由红色变成绿色,循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点,但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是 绿色 ,你 不能 在节点等待,必须离开。
第二小的值 是 严格大于 最小值的所有值中最小的值。
- 例如,
[2, 3, 4]中第二小的值是3,而[2, 2, 4]中第二小的值是4。
给你 n、edges、time 和 change ,返回从节点 1 到节点 n 需要的 第二短时间 。
注意:
- 你可以 任意次 穿过任意顶点,包括
1和n。 - 你可以假设在 启程时 ,所有信号灯刚刚变成 绿色 。
示例 1:
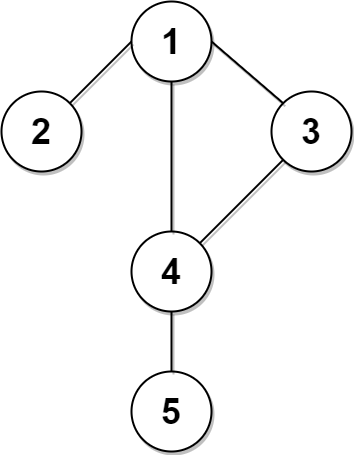
输入:n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出:13
解释:
上面的左图展现了给出的城市交通图。
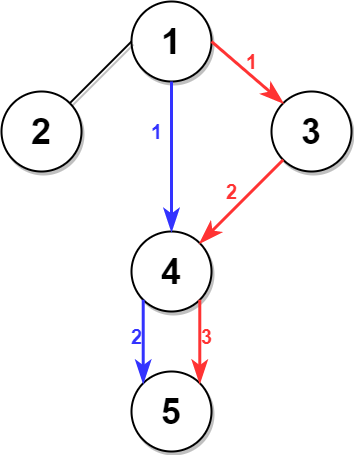
右图中的蓝色路径是最短时间路径。
花费的时间是:
- 从节点 1 开始,总花费时间=0
- 1 -> 4:3 分钟,总花费时间=3
- 4 -> 5:3 分钟,总花费时间=6
因此需要的最小时间是 6 分钟。
右图中的红色路径是第二短时间路径。
- 从节点 1 开始,总花费时间=0
- 1 -> 3:3 分钟,总花费时间=3
- 3 -> 4:3 分钟,总花费时间=6
- 在节点 4 等待 4 分钟,总花费时间=10
- 4 -> 5:3 分钟,总花费时间=13
因此第二短时间是 13 分钟。
示例 2:
输入:n = 2, edges = [[1,2]], time = 3, change = 2
输出:11
解释:
最短时间路径是 1 -> 2 ,总花费时间 = 3 分钟
第二短时间路径是 1 -> 2 -> 1 -> 2 ,总花费时间 = 11 分钟
提示:
2 <= n <= 104n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)edges[i].length == 21 <= ui, vi <= nui != vi- 不含重复边
- 每个节点都可以从其他节点直接或者间接到达
1 <= time, change <= 103
2、解题思路
- 将路径数组
edges转为邻接矩阵便于后续搜索- 转换过程中注意本题是双向连通图,任意边上的两个点都可以作为出发点
- 利用BFS求最短路径步数
min1和次短路径步数min2,BFS过程中需要注意剪枝:- 剪枝1:若
min2已经找到则退出 - 剪枝2:若从当前节点到达下一节点的步数
step+1与到达下一节点的最小步数minSteps.get(k)之差不小于2step + 1 - minSteps.get(k) >= 2,则跳过 - 剪枝3:同一层级每个节点只出现一次
- 剪枝1:若
- 按最短路径逐步叠加通过时间和等待红灯时间
这里剪枝的主要方式跟大多数题解不太一样,大部分题解都是利用节点不可能访问超过2次作为主要剪枝方式,确实没有想到这个点;这里主要利用次短路径与最短路径步数差值不超过2进行剪枝,原因是最短路径在任意节点上重复一个来回只需要2步,若次短路径的步数比最短路径多2步以上则说明其不能成为次短。
3、代码
var secondMinimum = function (n, edges, time, change) {
edges = edges.reduce((a, c) => {
// 双向连通图,建表时两个都可以作为出发点
!a[c[0]] ? (a[c[0]] = [c[1]]) : a[c[0]].push(c[1]);
!a[c[1]] ? (a[c[1]] = [c[0]]) : a[c[1]].push(c[0]);
return a;
}, new Array(n + 1));
let min1 = Infinity, min2 = Infinity, nodes = new Set([1]), step = 1;
const minSteps = new Map();
while (nodes.size && min2 === Infinity) {
const nextNodes = new Set();
for (const i of nodes) {
minSteps.set(i, step);
if (i === n) min1 === Infinity || min1 === step ? (min1 = step) : (min2 = step);
for (const k of edges[i]) {
if (minSteps.has(k) && step + 1 - minSteps.get(k) >= 2) continue;
nextNodes.add(k);
}
}
step++;
nodes = nextNodes;
}
let cost = 0;
for (let i = 1; i < Math.min(min1 + 2, min2); i++) {
if (((cost / change) >> 0) % 2) cost += change - (cost % change);
cost += time;
}
return cost;
};
4、执行结果
- 执行用时: 400 ms
- 内存消耗: 66.9 MB