131 篇博文 含有标签「数组」

1、题干​

设计一个算法：接收一个字符流，并检查这些字符的后缀是否是字符串数组 words 中的一个字符串。

例如，words = ["abc", "xyz"] 且字符流中逐个依次加入 4 个字符 'a'、'x'、'y' 和 'z' ，你所设计的算法应当可以检测到 "axyz" 的后缀 "xyz" 与 words 中的字符串 "xyz" 匹配。

按下述要求实现 StreamChecker 类：

• StreamChecker(String[] words) ：构造函数，用字符串数组 words 初始化数据结构。
• boolean query(char letter)：从字符流中接收一个新字符，如果字符流中的任一非空后缀能匹配 words 中的某一字符串，返回 true ；否则，返回 false。

示例：

输入：
["StreamChecker", "query", "query", "query", "query", "query", "query", "query", "query", "query", "query", "query", "query"]
[[["cd", "f", "kl"]], ["a"], ["b"], ["c"], ["d"], ["e"], ["f"], ["g"], ["h"], ["i"], ["j"], ["k"], ["l"]]
输出：
[null, false, false, false, true, false, true, false, false, false, false, false, true]

解释：
StreamChecker streamChecker = new StreamChecker(["cd", "f", "kl"]);
streamChecker.query("a"); // 返回 False
streamChecker.query("b"); // 返回 False
streamChecker.query("c"); // 返回n False
streamChecker.query("d"); // 返回 True ，因为 'cd' 在 words 中
streamChecker.query("e"); // 返回 False
streamChecker.query("f"); // 返回 True ，因为 'f' 在 words 中
streamChecker.query("g"); // 返回 False
streamChecker.query("h"); // 返回 False
streamChecker.query("i"); // 返回 False
streamChecker.query("j"); // 返回 False
streamChecker.query("k"); // 返回 False
streamChecker.query("l"); // 返回 True ，因为 'kl' 在 words 中

提示：

• 1 <= words.length <= 2000
• 1 <= words[i].length <= 200
• words[i] 由小写英文字母组成
• letter 是一个小写英文字母
• 最多调用查询 4 * 104 次

2、思路​

• 构造函数：字典树存储所有单词的逆序串
• query：数组存储字符流，按字符流逆序查找字典树中是否存在该后缀

3、代码​

class StreamChecker {
    letters = [];
    trie = { end: false };

    constructor(words: string[]) {
        for (const word of words) this.add(word);
    }

    query(letter: string): boolean {
        this.letters.push(letter);
        return this.find(this.letters);
    }

    add(word: string) {
        let t = this.trie;
        for (let i = word.length - 1; i > -1; i--) {
            if (!t[word[i]]) t[word[i]] = { end: false };
            t = t[word[i]];
        }
        t.end = true;
    }

    find(letters: string[]) {
        let t = this.trie;
        for (let i = letters.length - 1; i > -1; i--) {
            t = t[letters[i]];
            if (!t) return false;
            if (t.end) return true;
        }
        return t.end;
    }
}

4、复杂度​

• 时间复杂度：构造函数 $O(mn)$，query $O(mk)$，其中 n为单词数，m 为单词长度，k 为查询次数
• 空间复杂度：$O(mn+k)$

5、执行结果​

1、题干​

如果一个数列由至少两个元素组成，且每两个连续元素之间的差值都相同，那么这个序列就是 等差数列 。更正式地，数列 s 是等差数列，只需要满足：对于每个有效的 i ， s[i+1] - s[i] == s[1] - s[0] 都成立。

例如，下面这些都是 等差数列 ：

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

下面的数列 不是等差数列 ：

1, 1, 2, 5, 7

给你一个由 n 个整数组成的数组 nums，和两个由 m 个整数组成的数组 l 和 r，后两个数组表示 m 组范围查询，其中第 i 个查询对应范围 [l[i], r[i]] 。所有数组的下标都是 从 0 开始 的。

返回 boolean 元素构成的答案列表 answer 。如果子数组 nums[l[i]], nums[l[i]+1], ... , nums[r[i]] 可以 重新排列 形成 等差数列 ，answer[i] 的值就是 true；否则answer[i] 的值就是 false 。

示例 1：

输入：nums = [4,6,5,9,3,7], l = [0,0,2], r = [2,3,5]
输出：[true,false,true]
解释：
第 0 个查询，对应子数组 [4,6,5] 。可以重新排列为等差数列 [6,5,4] 。
第 1 个查询，对应子数组 [4,6,5,9] 。无法重新排列形成等差数列。
第 2 个查询，对应子数组 [5,9,3,7] 。可以重新排列为等差数列 [3,5,7,9] 。

示例 2：

输入：nums = [-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10], l = [0,1,6,4,8,7], r = [4,4,9,7,9,10]
输出：[false,true,false,false,true,true]

提示：

• n == nums.length
• m == l.length
• m == r.length
• 2 <= n <= 500
• 1 <= m <= 500
• 0 <= l[i] < r[i] < n
• -105 <= nums[i] <= 105

2、思路1​

模拟+计数排序

3、代码​

function checkArithmeticSubarrays(nums: number[], l: number[], r: number[]): boolean[] {
    const ans = new Array(l.length).fill(true);

    for (let i = 0; i < l.length; i++) {
        const len = r[i] - l[i] + 1;
        if (len < 3) continue;

        let min = 1e5, max = -1e5;
        for (let j = l[i]; j <= r[i]; j++) {
            min = Math.min(nums[j], min);
            max = Math.max(nums[j], max);
        }

        if (min === max) continue;

        const d = (max - min) / (len - 1);
        const buckt = new Array(len).fill(0);

        for (let j = l[i]; j <= r[i]; j++) {
            const m = (nums[j] - min) % d;
            const bi = (nums[j] - min) / d;
            if (m || buckt[bi]) {
                ans[i] = false;
                break;
            }
            buckt[bi] = 1;
        }
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

5、执行结果​

6、思路2​

模拟+排序API

7、代码​

function checkArithmeticSubarrays(nums: number[], l: number[], r: number[]): boolean[] {
    const ans = l.map(() => true);

    for (let i = 0; i < l.length; i++) {
        if (r[i] - l[i] < 2) continue;
        const arr = nums.slice(l[i], r[i] + 1).sort((a, b) => a - b);

        const d = arr[1] - arr[0];
        for (let j = 2; j < arr.length; j++) {
            if (arr[j] - arr[j - 1] !== d) {
                ans[i] = false;
                break;
            }
        }
    }

    return ans;
};

8、复杂度​

• 时间复杂度：$O(n^2 \log{n})$
• 空间复杂度：$O(n)$

9、执行结果​

1、题干​

骑士在一张 n x n 的棋盘上巡视。在 有效 的巡视方案中，骑士会从棋盘的 左上角 出发，并且访问棋盘上的每个格子 恰好一次 。

给你一个 n x n 的整数矩阵 grid ，由范围 [0, n * n - 1] 内的不同整数组成，其中 grid[row][col] 表示单元格 (row, col) 是骑士访问的第 grid[row][col] 个单元格。骑士的行动是从下标 0 开始的。

如果 grid 表示了骑士的有效巡视方案，返回 true；否则返回 false。

注意，骑士行动时可以垂直移动两个格子且水平移动一个格子，或水平移动两个格子且垂直移动一个格子。下图展示了骑士从某个格子出发可能的八种行动路线。

示例 1：

输入：grid = [[0,11,16,5,20],[17,4,19,10,15],[12,1,8,21,6],[3,18,23,14,9],[24,13,2,7,22]]
输出：true
解释：grid 如上图所示，可以证明这是一个有效的巡视方案。

示例 2：

输入：grid = [[0,3,6],[5,8,1],[2,7,4]]
输出：false
解释：grid 如上图所示，考虑到骑士第 7 次行动后的位置，第 8 次行动是无效的。

提示：

• n == grid.length == grid[i].length
• 3 <= n <= 7
• 0 <= grid[row][col] < n * n
• grid 中的所有整数 互不相同

2、思路​

从左上角开始 DFS 遍历，如果能完成遍历则说明巡视方案有效

3、代码​

function checkValidGrid(grid: number[][]): boolean {
    let vis = 0;
    const dirs = [[-2, -1], [2, 1], [-2, 1], [2, -1], [-1, -2], [1, 2], [-1, 2], [1, -2]];
    const t = grid.length * grid[0].length;

    function dfs(r: number, c: number) {
        vis++;
        if (grid[r][c] === t - 1) return;

        for (const [dr, dc] of dirs) {
            if (grid[r + dr]?.at(c + dc) === grid[r][c] + 1) {
                dfs(r + dr, c + dc);
                break;
            }
        }
    }

    dfs(0, 0);

    return vis === t;
};

4、复杂度​

• 时间复杂度： $O(n^2)$
• 空间复杂度： $O(n^2)$

5、执行结果​

1、题干​

给你一个由正整数组成的数组 nums 和一个 正 整数 k 。

如果 nums 的子集中，任意两个整数的绝对差均不等于 k ，则认为该子数组是一个 美丽 子集。

返回数组 nums 中 非空 且 美丽 的子集数目。

nums 的子集定义为：可以经由 nums 删除某些元素（也可能不删除）得到的一个数组。只有在删除元素时选择的索引不同的情况下，两个子集才会被视作是不同的子集。

示例 1：

输入：nums = [2,4,6], k = 2
输出：4
解释：数组 nums 中的美丽子集有：[2], [4], [6], [2, 6] 。
可以证明数组 [2,4,6] 中只存在 4 个美丽子集。

示例 2：

输入：nums = [1], k = 1
输出：1
解释：数组 nums 中的美丽数组有：[1] 。
可以证明数组 [1] 中只存在 1 个美丽子集。 

提示：

• 1 <= nums.length <= 20
• 1 <= nums[i], k <= 1000

2、思路​

BFS暴力枚举，时间爆炸，有空再优化，下次一定

3、代码​

function beautifulSubsets(nums: number[], k: number): number {
    const hash = new Array(nums.length).fill(0).map(() => new Array(nums.length).fill(0))
    for (let i = 0; i < nums.length; i++) {
        for (let j = i + 1; j < nums.length; j++) {
            if (Math.abs(nums[j] - nums[i]) === k) hash[i][j] = 1;
        }
    }

    let queue = nums.map((v, i) => [i]), ans = 0;
    while (queue.length) {
        const next = [];
        for (const q of queue) {
            ans++;
            for (let j = q.at(-1) + 1; j < nums.length; j++) {
                if (q.every((i) => !hash[i][j])) next.push([...q, j]);
            }
        }
        queue = next;
    }

    return ans;
};

4、执行结果​

1、题干​

给你一个下标从 0 开始的整数数组 nums 和一个整数 value 。

在一步操作中，你可以对 nums 中的任一元素加上或减去 value 。

• 例如，如果 nums = [1,2,3] 且 value = 2 ，你可以选择 nums[0] 减去 value ，得到 nums = [-1,2,3] 。

数组的 MEX (minimum excluded) 是指其中数组中缺失的最小非负整数。

• 例如，[-1,2,3] 的 MEX 是 0 ，而 [1,0,3] 的 MEX 是 2 。

返回在执行上述操作 任意次 后，nums 的最大 MEX 。

示例 1：

输入：nums = [1,-10,7,13,6,8], value = 5
输出：4
解释：执行下述操作可以得到这一结果：
- nums[1] 加上 value 两次，nums = [1,0,7,13,6,8]
- nums[2] 减去 value 一次，nums = [1,0,2,13,6,8]
- nums[3] 减去 value 两次，nums = [1,0,2,3,6,8]
nums 的 MEX 是 4 。可以证明 4 是可以取到的最大 MEX 。

示例 2：

输入：nums = [1,-10,7,13,6,8], value = 7
输出：2
解释：执行下述操作可以得到这一结果：
- nums[2] 减去 value 一次，nums = [1,-10,0,13,6,8]
nums 的 MEX 是 2 。可以证明 2 是可以取到的最大 MEX 。

提示：

• 1 <= nums.length, value <= 105
• -109 <= nums[i] <= 109

2、思路​

• 对 nums 所有元素与 value 取模计数，得到数组 ms
• 遍历区间 [0,nums.length)，消费 ms，直到遍历结束 或 ms 中某个余数被消耗完（ms[i % value] < 1） ，此时的下标 i 即所求结果

3、代码​

function findSmallestInteger(nums: number[], value: number): number {
    const ms = new Array(value).fill(0);
    for (const n of nums) {
        const mod = n % value + (n % value < 0 ? value : 0);
        ms[mod]++;
    }

    let ans = 0;
    for (let i = 0; i < nums.length; i++, ans++) {
        const mod = i % value;
        if (ms[mod] < 1) break;
        ms[mod]--;
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

5、执行结果​

1、题干​

给你一个长度为 n 的整数数组 nums ，和一个长度为 m 的整数数组 queries 。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是 nums 中 元素之和小于等于 queries[i] 的 子序列 的 最大 长度  。

子序列 是由一个数组删除某些元素（也可以不删除）但不改变剩余元素顺序得到的一个数组。

示例 1：

输入：nums = [4,5,2,1], queries = [3,10,21]
输出：[2,3,4]
解释：queries 对应的 answer 如下：
- 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ，所以 answer[0] = 2 。
- 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ，所以 answer[1] = 3 。
- 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ，所以 answer[2] = 4 。

示例 2：

输入：nums = [2,3,4,5], queries = [1]
输出：[0]
解释：空子序列是唯一一个满足元素和小于或等于 1 的子序列，所以 answer[0] = 0 。

提示：

• n == nums.length
• m == queries.length
• 1 <= n, m <= 1000
• 1 <= nums[i], queries[i] <= 106

2、思路1-暴力​

• 对 nums 升序排序，求前缀和
• 暴力查找不大于 queries[i] 的前缀和数量

3、代码​

function answerQueries(nums: number[], queries: number[]): number[] {
    nums.sort((a, b) => a - b);
    for (let i = 1; i < nums.length; i++) nums[i] += nums[i - 1];

    let ans = queries.map(Number);
    for (let i = 0; i < queries.length; i++) {
        if (nums.at(-1) <= queries[i]) ans[i] = nums.length;
        else ans[i] = nums.findIndex((s) => s > queries[i]);
    }

    return ans;
};

4、复杂度​

• 时间复杂度： $O(n^2)$
• 空间复杂度： $O(\log{n})$

5、执行结果​

6、思路2-排序优化​

在思路1的基础上进行优化，如果 queries 是升序数组，那么查找子序列就不用每次都从头到尾遍历前缀和数组，可以从上一个找到的前缀和下标开始往后查找，查找过程复杂度从 $O(n^2)$ 降到 $O(n)$

7、代码​

function answerQueries(nums: number[], queries: number[]): number[] {
    nums.sort((a, b) => a - b);
    for (let i = 1; i < nums.length; i++) nums[i] += nums[i - 1];

    const qs = queries.map((n, i) => [n, i]).sort((a, b) => a[0] - b[0]);

    let ans = queries.map(Number);
    for (let i = 0, j = 0; i < qs.length; i++) {
        if (nums.at(-1) <= qs[i][0]) {
            ans[qs[i][1]] = nums.length;
            continue;
        }

        while (nums[j] <= qs[i][0]) j++;
        ans[qs[i][1]] = j;
    }

    return ans;
};

8、复杂度​

• 时间复杂度： $O(n \log{n})$
• 空间复杂度： $O(n)$

9、执行结果​

1、题干​

给你一个长度为 n 的数组 nums ，该数组由从 1 到 n 的 不同 整数组成。另给你一个正整数 k 。

统计并返回 nums 中的 中位数 等于 k 的非空子数组的数目。

注意：

• 数组的中位数是按 递增 顺序排列后位于 中间 的那个元素，如果数组长度为偶数，则中位数是位于中间靠 左 的那个元素。
  • 例如，[2,3,1,4] 的中位数是 2 ，[8,4,3,5,1] 的中位数是 4 。
• 子数组是数组中的一个连续部分。

示例 1：

输入：nums = [3,2,1,4,5], k = 4
输出：3
解释：中位数等于 4 的子数组有：[4]、[4,5] 和 [1,4,5] 。

示例 2：

输入：nums = [2,3,1], k = 3
输出：1
解释：[3] 是唯一一个中位数等于 3 的子数组。

提示：

• n == nums.length
• 1 <= n <= 105
• 1 <= nums[i], k <= n
• nums 中的整数互不相同

整得有点复杂，错了几次，裂开

2、思路​

对于任意包含 k 的子数组符合要求的条件是：假设小于 k 的数有 cl个，大于 k 的数有 cr个，只要满足 cl === cr 或者 cl + 1 === cr 即可

以 k 的下标 ki 为界限，考虑三类子数组情况：

• 左半边子数组符合要求
• 右半边子数组符合要求
• 左右两边子数组组合后符合要求

前两类情况在 $O(n)$ 时间复杂度内可以出结果，第三类情况如果暴力求解，时间复杂度会达到$O(n^2)$，用哈希表优化可以做到 $O(n)$

3、代码​

function countSubarrays(nums: number[], k: number): number {
    const ki = nums.indexOf(k), om = new Map(), em = new Map();
    let ans = 0, sum = 0;
    for (let i = ki - 1; i > -1; i--) {
        sum += nums[i] < k ? -1 : 1;
        if (!sum || sum === 1) ans++;

        const map = i % 2 ? om : em;
        map.set(sum, (map.get(sum) || 0) + 1);
    }

    sum = 0;
    for (let i = ki + 1; i < nums.length; i++) {
        sum += nums[i] < k ? -1 : 1;
        if (!sum || sum === 1) ans++;

        let map = i % 2 ? om : em;
        if (map.get(-sum)) ans += map.get(-sum);

        map = i % 2 ? em : om;
        if (map.get(1 - sum)) ans += map.get(1 - sum);
    }

    return ans + 1;
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

5、执行结果​

1、题干​

给你一个下标从 0 开始的整数数组 nums ，请你找出一个下标从 0 开始的整数数组 answer ，其中：

• answer.length == nums.length
• answer[i] = |leftSum[i] - rightSum[i]|

其中：

• leftSum[i] 是数组 nums 中下标 i 左侧元素之和。如果不存在对应的元素，leftSum[i] = 0 。
• rightSum[i] 是数组 nums 中下标 i 右侧元素之和。如果不存在对应的元素，rightSum[i] = 0 。

返回数组 answer 。

示例 1：

输入：nums = [10,4,8,3]
输出：[15,1,11,22]
解释：数组 leftSum 为 [0,10,14,22] 且数组 rightSum 为 [15,11,3,0] 。
数组 answer 为 [|0 - 15|,|10 - 11|,|14 - 3|,|22 - 0|] = [15,1,11,22] 。

示例 2：

输入：nums = [1]
输出：[0]
解释：数组 leftSum 为 [0] 且数组 rightSum 为 [0] 。
数组 answer 为 [|0 - 0|] = [0] 。

提示：

• 1 <= nums.length <= 1000
• 1 <= nums[i] <= 105

2、思路​

计算前缀和与总和，遍历求得结果

3、代码​

function leftRigthDifference(nums: number[]): number[] {
    const sum = nums.reduce((a, c) => a + c, 0);

    for (let i = 0, ls = 0; i < nums.length; i++) {
        ls += nums[i];
        nums[i] = Math.abs(ls - nums[i] - (sum - ls));
    }

    return nums;
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

5、执行结果​

1、题干​

给你两个非负整数数组 rowSum 和 colSum ，其中 rowSum[i] 是二维矩阵中第 i 行元素的和， colSum[j] 是第 j 列元素的和。换言之你不知道矩阵里的每个元素，但是你知道每一行和每一列的和。

请找到大小为 rowSum.length x colSum.length 的任意 非负整数 矩阵，且该矩阵满足 rowSum 和 colSum 的要求。

请你返回任意一个满足题目要求的二维矩阵，题目保证存在 至少一个 可行矩阵。

示例 1：

输入：rowSum = [3,8], colSum = [4,7]
输出：[[3,0],
      [1,7]]
解释：
第 0 行：3 + 0 = 3 == rowSum[0]
第 1 行：1 + 7 = 8 == rowSum[1]
第 0 列：3 + 1 = 4 == colSum[0]
第 1 列：0 + 7 = 7 == colSum[1]
行和列的和都满足题目要求，且所有矩阵元素都是非负的。
另一个可行的矩阵为：[[1,2],
                  [3,5]]

示例 2：

输入：rowSum = [5,7,10], colSum = [8,6,8]
输出：[[0,5,0],
      [6,1,0],
      [2,0,8]]

示例 3：

输入：rowSum = [14,9], colSum = [6,9,8]
输出：[[0,9,5],
      [6,0,3]]

示例 4：

输入：rowSum = [1,0], colSum = [1]
输出：[[1],
      [0]]

示例 5：

输入：rowSum = [0], colSum = [0]
输出：[[0]]

提示：

• 1 <= rowSum.length, colSum.length <= 500
• 0 <= rowSum[i], colSum[i] <= 108
• sum(rowSum) == sum(colSum)

以为是个回溯，没想到是个贪心，磨蹭半天才想到，还不是最优的思路

2、思路1​

• 生成元素全为 0 的矩阵 grid，grid[0] 初始化为 colSum
• 遍历所有行的元素（最后一行除外），通过 rowSum[i] 的约束将超出的数转移到下一行

3、代码​

function restoreMatrix(rowSum: number[], colSum: number[]): number[][] {
    const grid = rowSum.map(() => colSum.map(() => 0));
    grid[0] = colSum;

    for (let i = 0; i < rowSum.length - 1; i++) {
        let sum = grid[i].reduce((a, c) => a + c, 0);
        for (let j = 0; j < colSum.length && sum > rowSum[i]; j++) {
            grid[i + 1][j] = Math.min(sum - rowSum[i], grid[i][j]);
            grid[i][j] -= grid[i + 1][j];
            sum -= grid[i + 1][j];
        }
    }

    return grid;
};

4、复杂度​

• 时间复杂度：$O(mn)$
• 空间复杂度：$O(1)$

5、执行结果​

6、思路2​

更直接的贪心，通过 rowSum[i] 与 colSum[j] 直接约束 grid[i][j]

7、代码​

function restoreMatrix(rowSum: number[], colSum: number[]): number[][] {
    const grid = rowSum.map(() => colSum.map(() => 0));

    for (let i = 0; i < rowSum.length; i++) {
        for (let j = 0; j < colSum.length; j++) {
            grid[i][j] = Math.min(rowSum[i], colSum[j]);
            rowSum[i] -= grid[i][j];
            colSum[j] -= grid[i][j];
        }
    }

    return grid;
};

8、复杂度​

• 时间复杂度：$O(mn)$
• 空间复杂度：$O(1)$

9、执行结果​

1、题干​

你正在参加一场比赛，给你两个 正 整数 initialEnergy 和 initialExperience 分别表示你的初始精力和初始经验。

另给你两个下标从 0 开始的整数数组 energy 和 experience，长度均为 n 。

你将会 依次 对上 n 个对手。第 i 个对手的精力和经验分别用 energy[i] 和 experience[i] 表示。当你对上对手时，需要在经验和精力上都 严格 超过对手才能击败他们，然后在可能的情况下继续对上下一个对手。

击败第 i 个对手会使你的经验 增加 experience[i]，但会将你的精力 减少  energy[i] 。

在开始比赛前，你可以训练几个小时。每训练一个小时，你可以选择将增加经验增加 1 或者 将精力增加 1 。

返回击败全部 n 个对手需要训练的 最少 小时数目。

示例 1：

输入：initialEnergy = 5, initialExperience = 3, energy = [1,4,3,2], experience = [2,6,3,1]
输出：8
解释：在 6 小时训练后，你可以将精力提高到 11 ，并且再训练 2 个小时将经验提高到 5 。
按以下顺序与对手比赛：
- 你的精力与经验都超过第 0 个对手，所以获胜。
  精力变为：11 - 1 = 10 ，经验变为：5 + 2 = 7 。
- 你的精力与经验都超过第 1 个对手，所以获胜。
  精力变为：10 - 4 = 6 ，经验变为：7 + 6 = 13 。
- 你的精力与经验都超过第 2 个对手，所以获胜。
  精力变为：6 - 3 = 3 ，经验变为：13 + 3 = 16 。
- 你的精力与经验都超过第 3 个对手，所以获胜。
  精力变为：3 - 2 = 1 ，经验变为：16 + 1 = 17 。
在比赛前进行了 8 小时训练，所以返回 8 。
可以证明不存在更小的答案。

示例 2：

输入：initialEnergy = 2, initialExperience = 4, energy = [1], experience = [3]
输出：0
解释：你不需要额外的精力和经验就可以赢得比赛，所以返回 0 。

提示：

• n == energy.length == experience.length
• 1 <= n <= 100
• 1 <= initialEnergy, initialExperience, energy[i], experience[i] <= 100

2、思路​

需要增加的精力值是：energy 数组总和超出 initialEnergy 的部分再加 1，即 max(sum(energy) - initialEnergy + 1, 0)

需要增加的经验值是：experience 中所有元素超出 initialExperience 的部分再加 1，即 sum(max(experience[i] - initialExperience + 1, 0))

计算经验值的过程中，initialExperience 需要累加已经比较过的 experience[i]

3、代码​

function minNumberOfHours(initialEnergy: number, initialExperience: number, energy: number[], experience: number[]): number {
    const se = energy.reduce((a, c) => a + c, 0);
    let ans = se < initialEnergy ? 0 : se - initialEnergy + 1;

    for (const e of experience) {
        if (initialExperience <= e) {
            ans += e - initialExperience + 1;
            initialExperience = e + 1;
        }
        initialExperience += e;
    }

    return ans;
};

4、复杂度​

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

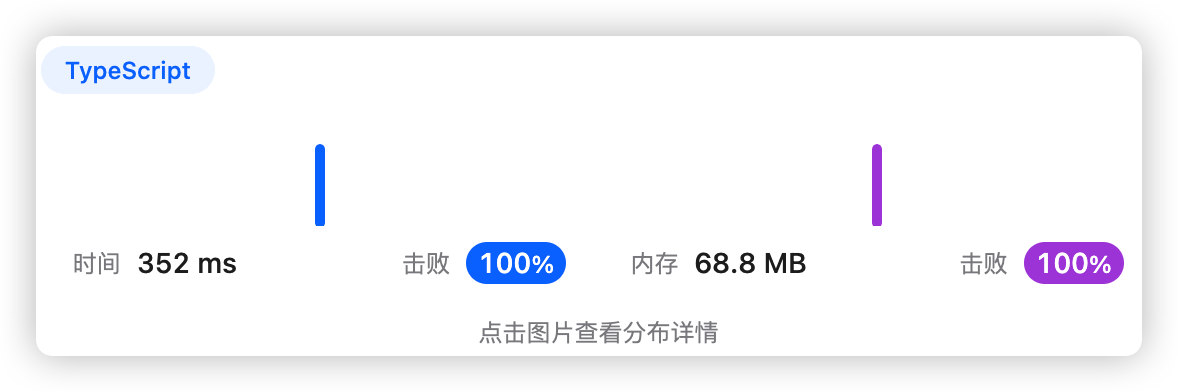
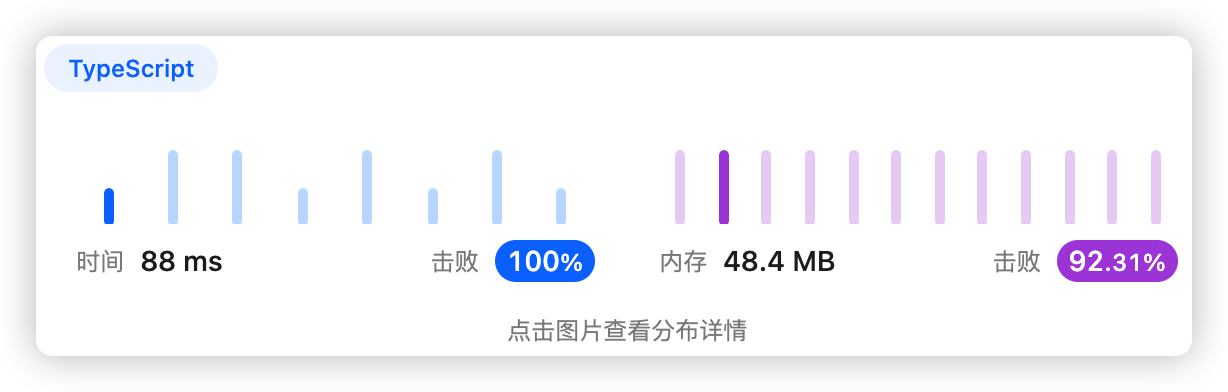
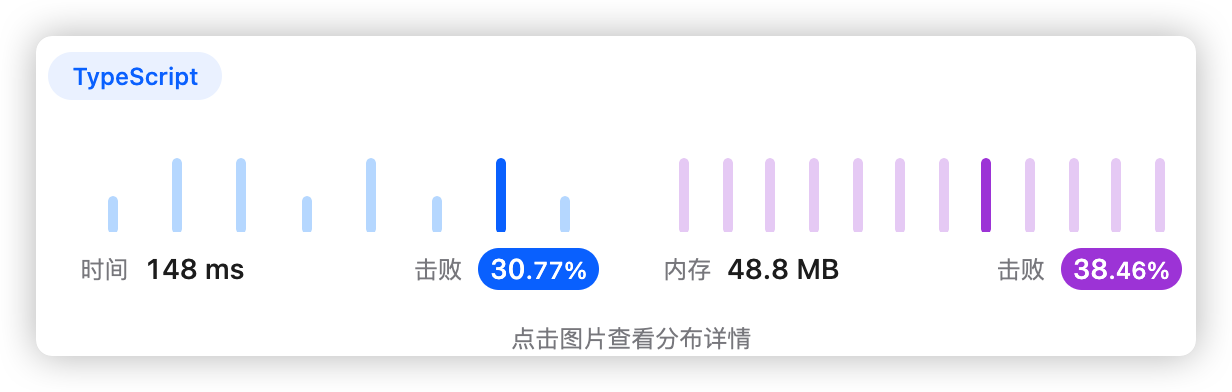
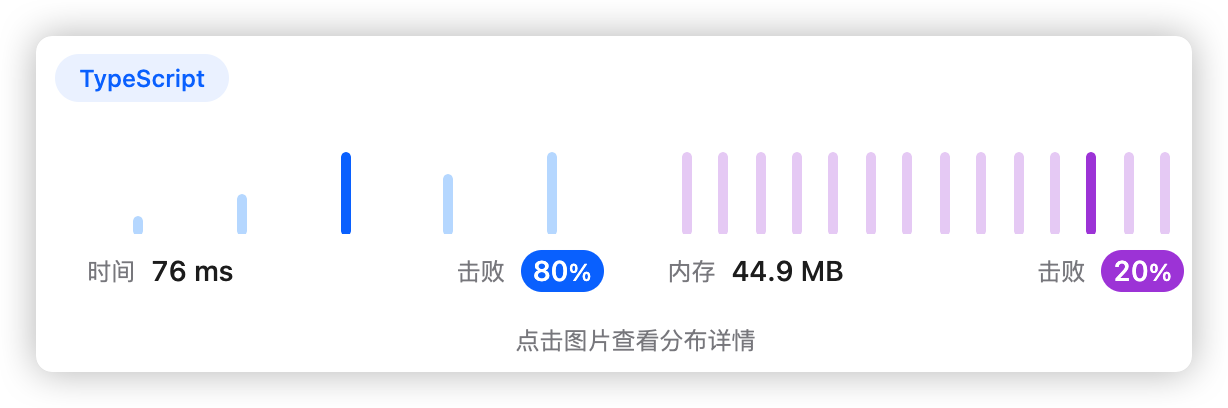
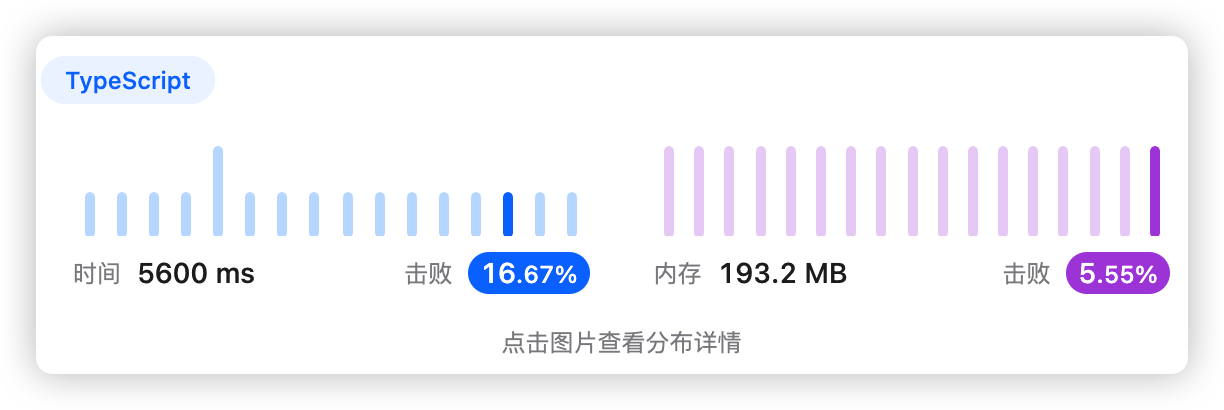
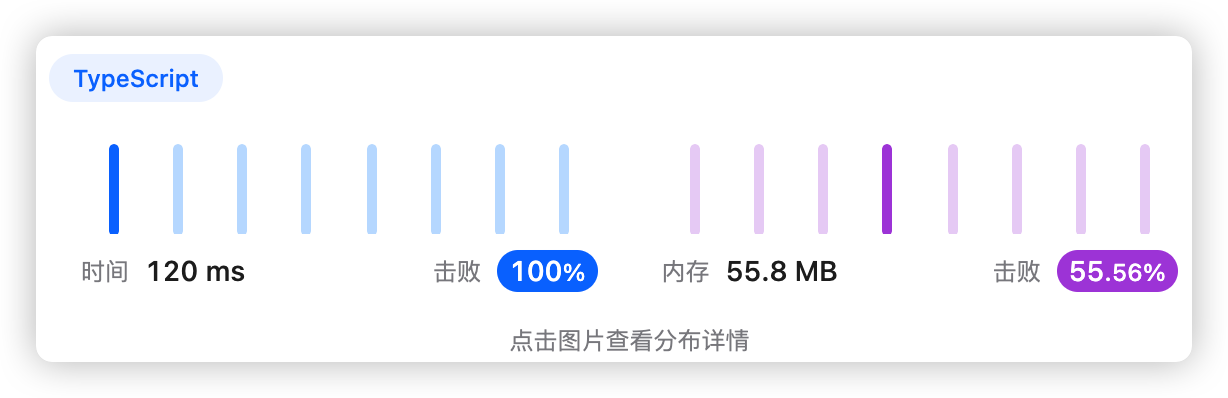
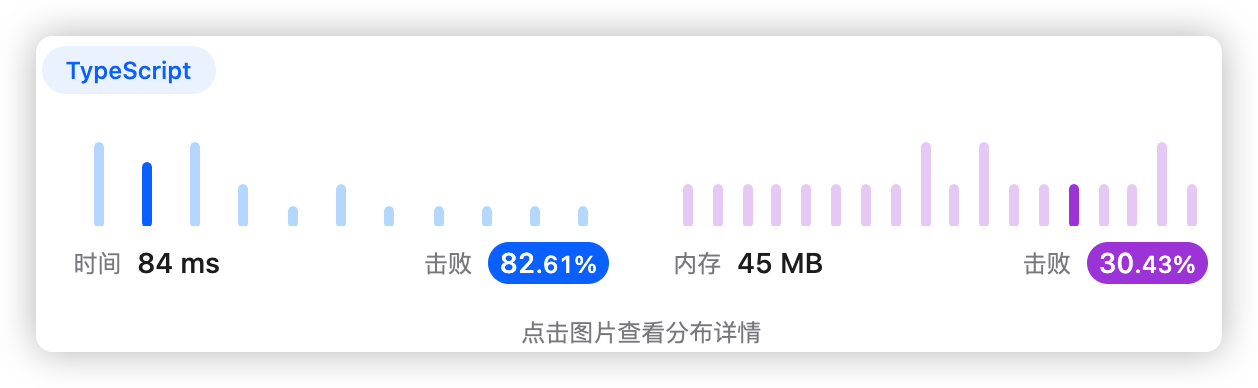
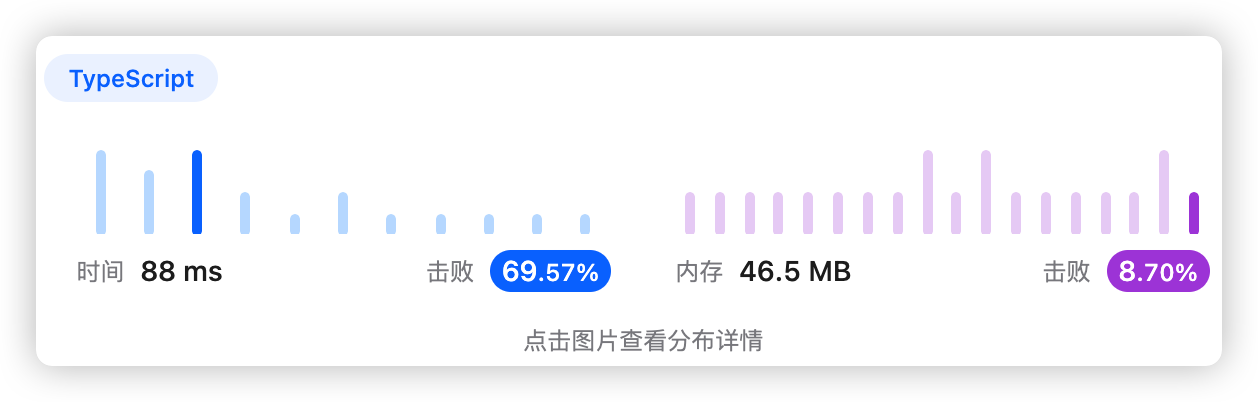
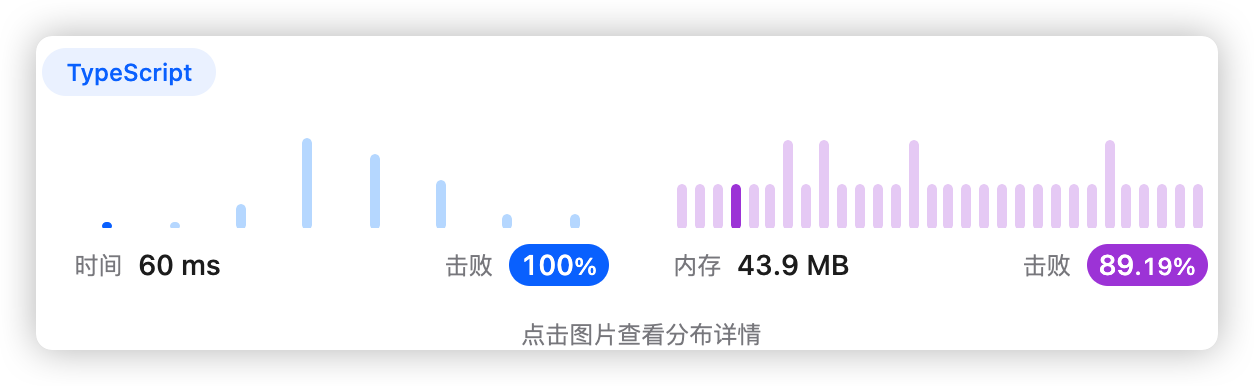
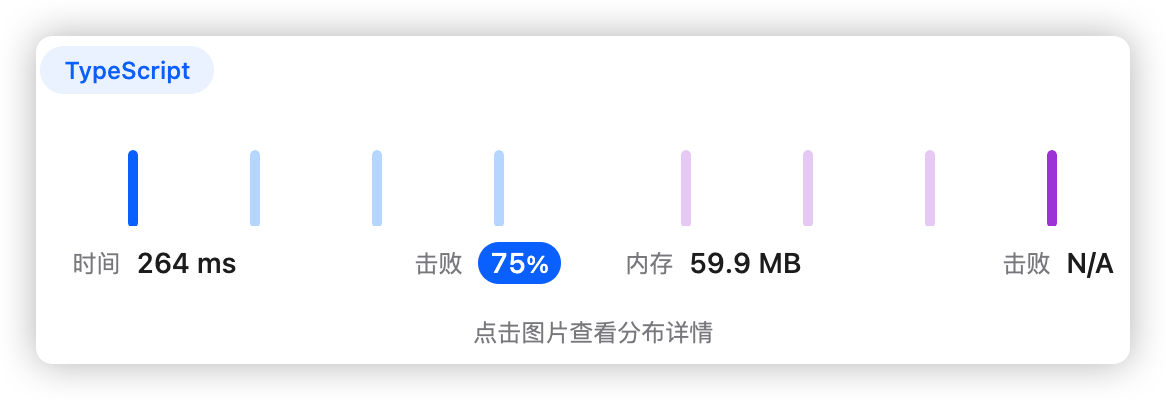
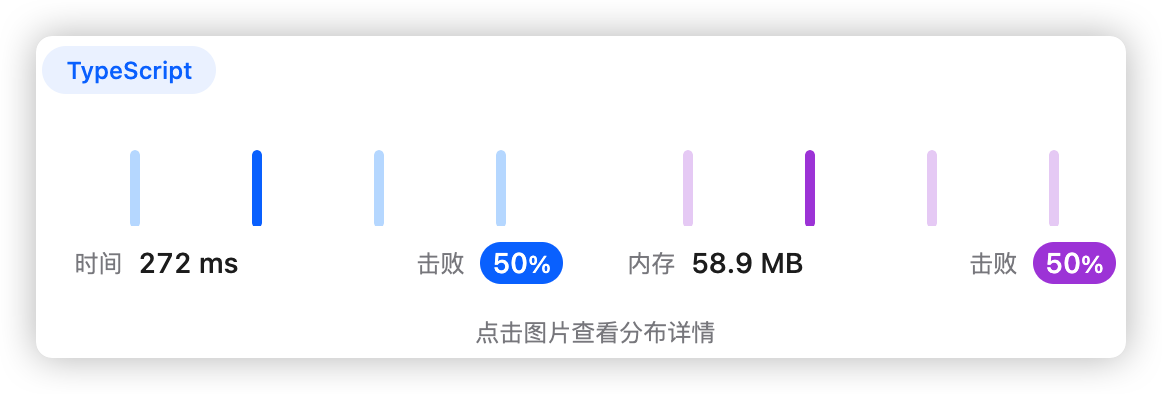
5、执行结果​