1、题干
在一个 106 x 106 的网格中,每个网格上方格的坐标为 (x, y) 。
现在从源方格 source = [sx, sy] 开始出发,意图赶往目标方格 target = [tx, ty] 。数组 blocked 是封锁的方格列表,其中每个 blocked[i] = [xi, yi] 表示坐标为 (xi, yi) 的方格是禁止通行的。
每次移动,都可以走到网格中在四个方向上相邻的方格,只要该方格 不 在给出的封锁列表 blocked 上。同时,不允许走出网格。
只有在可以通过一系列的移动从源方格 source 到达目标方格 target 时才返回 true。否则,返回 false。
示例 1:
输入:blocked = [[0,1],[1,0]], source = [0,0], target = [0,2]
输出:false
解释:
从源方格无法到达目标方格,因为我们无法在网格中移动。
无法向北或者向东移动是因为方格禁止通行。
无法向南或者向西移动是因为不能走出网格。示例 2:
输入:blocked = [], source = [0,0], target = [999999,999999]
输出:true
解释:
因为没有方格被封锁,所以一定可以到达目标方格。
提示:
0 <= blocked.length <= 200blocked[i].length == 20 <= xi, yi < 106source.length == target.length == 20 <= sx, sy, tx, ty < 106source != target- 题目数据保证
source和target不在封锁列表内
2、解题思路
迷宫的封锁列表blocked会形成围栏,假设从起点和终点分别进行深度遍历,遍历过程中设定步数最大值steps为围栏最大面积,若2条路径行进的步数都超过最大步数或者遍历过程中起点和终点都能访问到则表示起止点连通,则表示起止点连通,反之不连通。
注意点
- 最开始认为围栏的最大面积是,是一块正方形区域。实际官解给出的是,是一块等腰直角三角形区域,其中
n为blocked数组长度。具体实现时没看官解,限制的是,实际上围栏最大面积略偏高不影响结果,因为在不被围的情况下可以走的步数肯定远超这个值。这个最大面积的推导和精确计算可以说有点复杂了,答题时被用例28教育了一番。 - 遍历过程中如果起止两个点都能访问到则表示起止点连通(用例
[[0,3],[1,0],[1,1],[1,2],[1,3]] [0,0] [0,2]) - 走过的坐标使用哈希表记录,以免重复遍历导致死循环
- JS若使用递归实现在执行用例28时会出现栈溢出(本地溢出,力扣判题程序未溢出,后面补充了递归DFS代码)
3、代码-非递归
var isEscapePossible = function (blocked, source, target) {
const hash = (x, y) => 1123 * x + y;
const maxSteps = blocked.length ** 2 / 2, dirs = [[0, 1], [0, -1], [1, 0], [-1, 0]];
const blockSet = blocked.reduce((a, c) => a.add(hash(c[0], c[1])), new Set());
function move(s, t, steps, visited) {
const stack = [s];
while (stack.length) {
const [x, y] = stack.pop();
if (x < 0 || x >= 1e6 || y < 0 || y >= 1e6 || blockSet.has(hash(x, y)) || visited.has(hash(x, y))) continue;
if (--steps <= 0 || (x === t[0] && y === t[1])) return true;
visited.add(hash(x, y));
for (const d of dirs) stack.push([x + d[0], y + d[1]]);
}
return false;
}
return move(source, target, maxSteps, new Set()) && move(target, source, maxSteps, new Set());
};
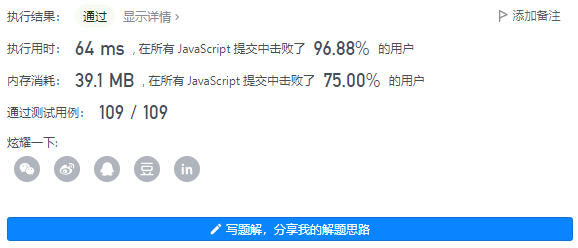
4、执行结果
执行用时: 156 ms 内存消耗: 58.8 MB
5、代码-递归
var isEscapePossible = function (blocked, source, target) {
const hash = (x, y) => 1123 * x + y;
const maxSteps = blocked.length ** 2 / 2, dirs = [[0, 1], [0, -1], [1, 0], [-1, 0]];
const blockSet = blocked.reduce((a, c) => a.add(hash(c[0], c[1])), new Set());
function dfs(x, y, steps, visited, t) {
if (x < 0 || x >= 1e6 || y < 0 || y >= 1e6 || blockSet.has(hash(x, y)) || visited.has(hash(x, y))) return false;
if (--steps <= 0 || (x === t[0] && y === t[1])) return true;
visited.add(hash(x, y));
return dirs.reduce((a, c) => a || dfs(x + c[0], y + c[1], steps, visited, t), false);
}
return dfs(...source, maxSteps, new Set(), target) && dfs(...target, maxSteps, new Set(), source);
};
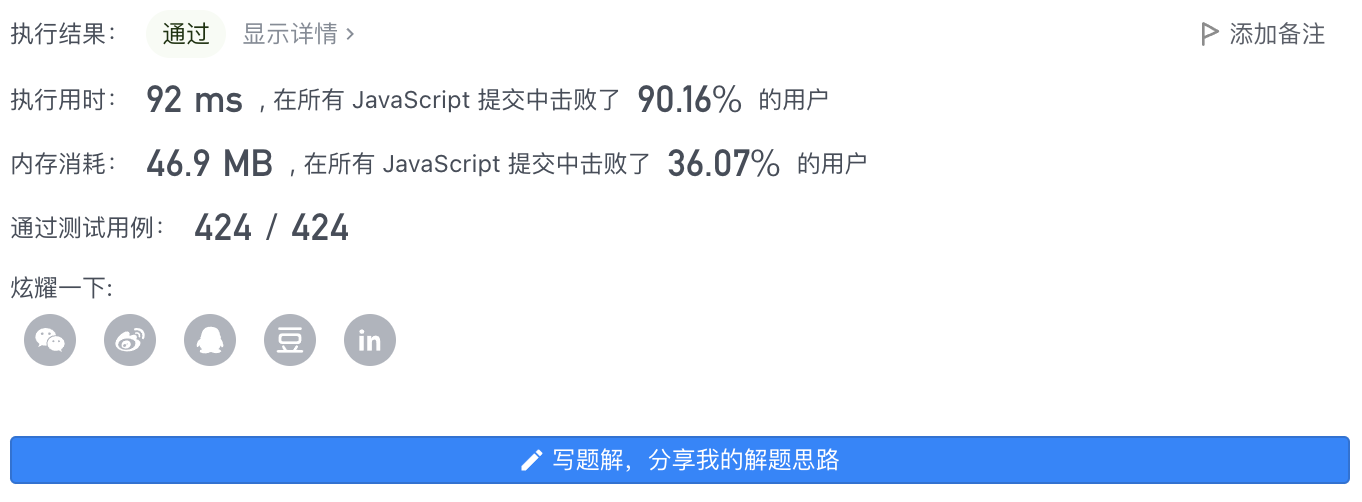
6、执行结果
执行用时: 120 ms 内存消耗: 47.8 MB

7、优化点
- 问题:最开始哈希表保存的坐标是字符串拼接而来,但是字符串消耗空间更多、操作耗时更多,所以执行结果的时长和内存偏高
- 优化:不用字符串做key,使用质数乘法把坐标转成唯一数字,使用该唯一数字做key
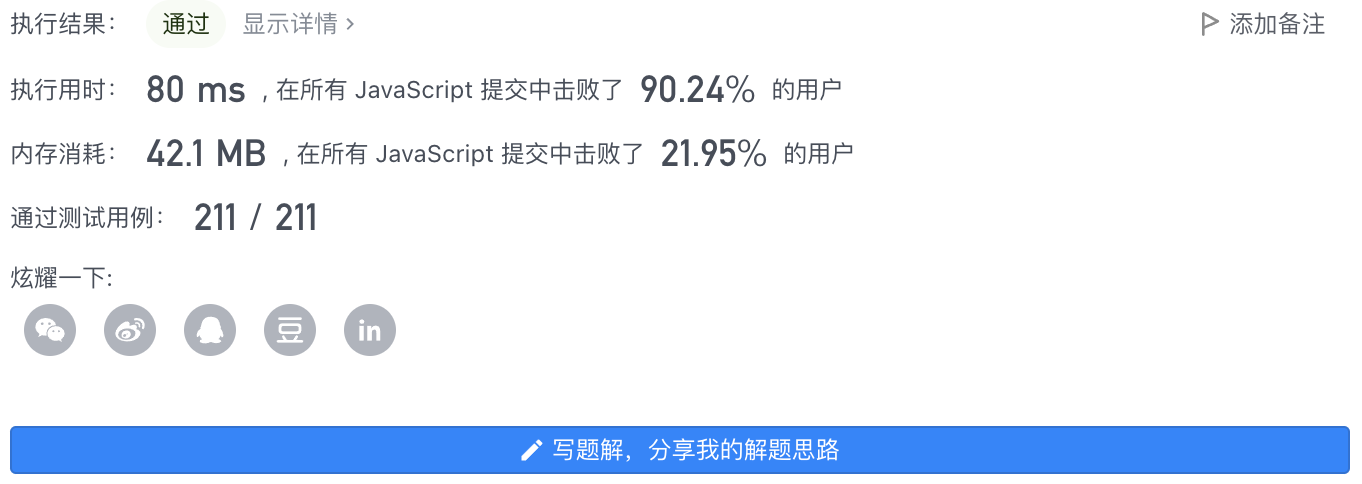
- 结果:优化后两种代码执行结果用时减半(240ms 到 120ms),内存消耗也大幅减少(57.3 MB 到 47.8 MB),递归DFS代码执行结果破双百
字符串做key比较容易理解和实现且不会冲突,但消耗时间空间较多;而数字做key的好处在于消耗时间空间较少,但麻烦点在于实现时要注意避免key冲突的问题。