你还记得那条风靡全球的贪吃蛇吗?
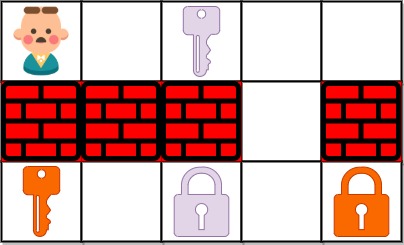
我们在一个 n*n 的网格上构建了新的迷宫地图,蛇的长度为 2,也就是说它会占去两个单元格。蛇会从左上角((0, 0) 和 (0, 1))开始移动。我们用 0 表示空单元格,用 1 表示障碍物。蛇需要移动到迷宫的右下角((n-1, n-2) 和 (n-1, n-1))。
每次移动,蛇可以这样走:
- 如果没有障碍,则向右移动一个单元格。并仍然保持身体的水平/竖直状态。
- 如果没有障碍,则向下移动一个单元格。并仍然保持身体的水平/竖直状态。
- 如果它处于水平状态并且其下面的两个单元都是空的,就顺时针旋转 90 度。蛇从(
(r, c)、(r, c+1))移动到 ((r, c)、(r+1, c))。
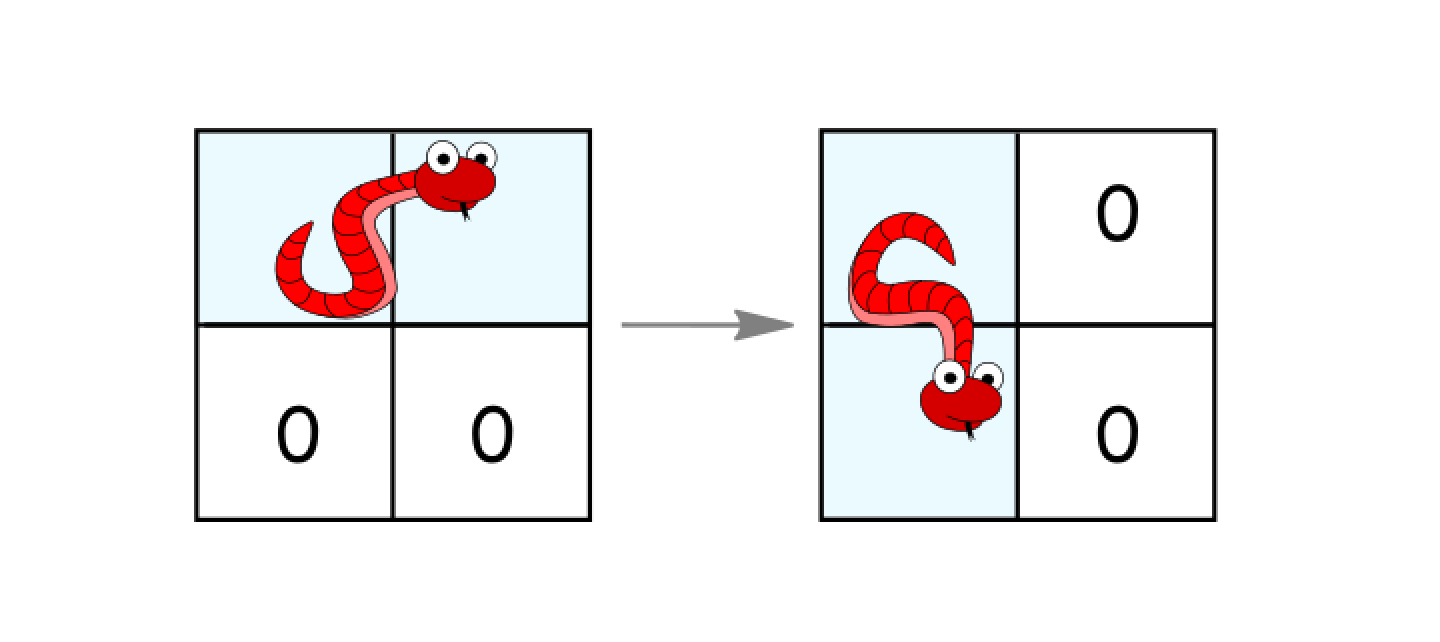
- 如果它处于竖直状态并且其右面的两个单元都是空的,就逆时针旋转 90 度。蛇从(
(r, c)、(r+1, c))移动到((r, c)、(r, c+1))。
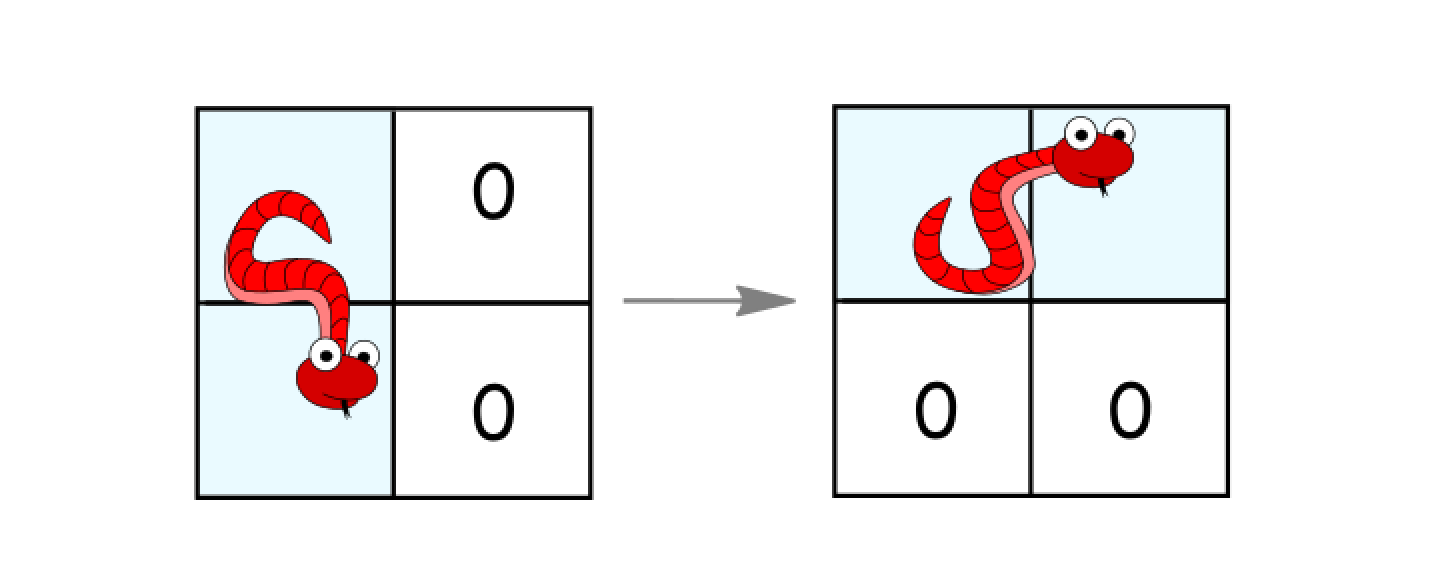
返回蛇抵达目的地所需的最少移动次数。
如果无法到达目的地,请返回 -1。
示例 1:
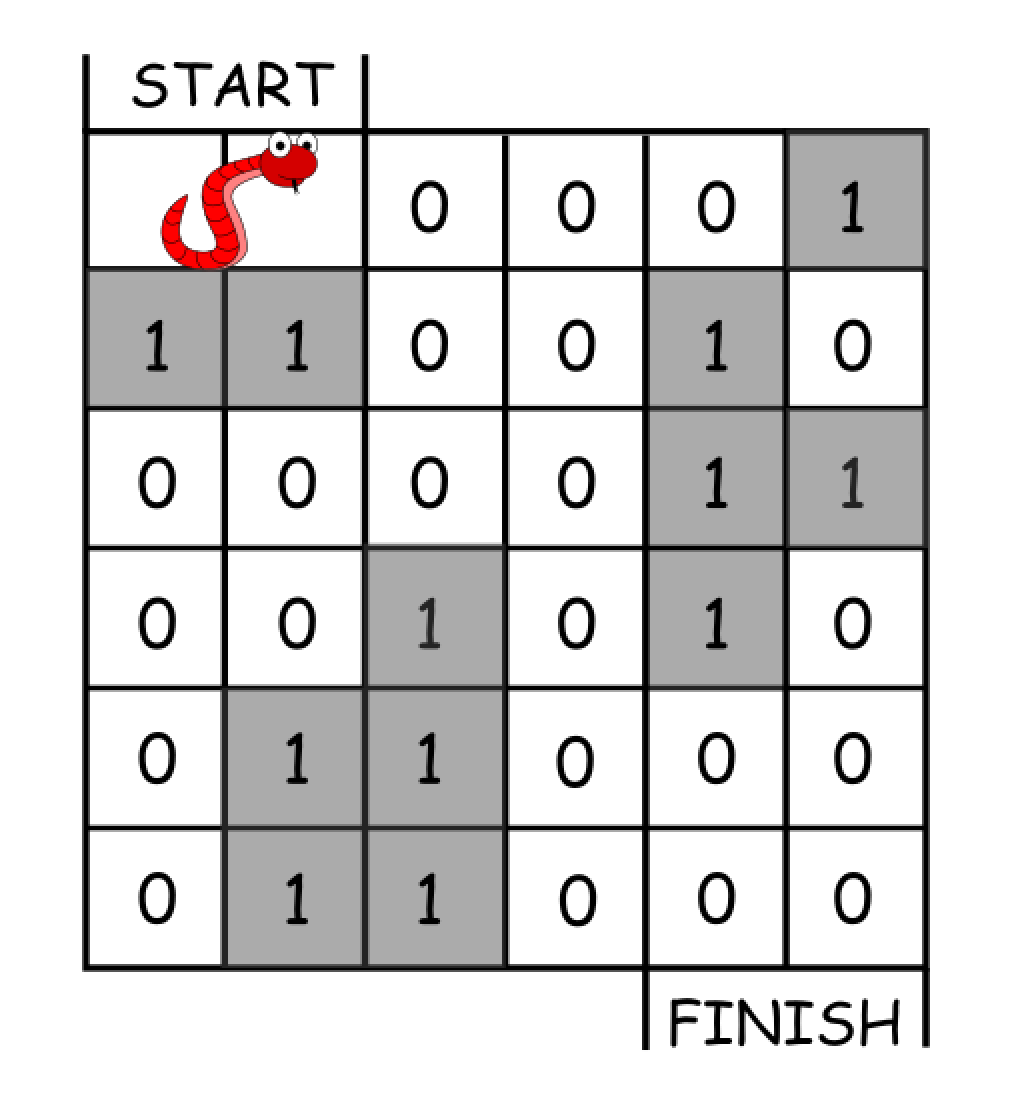
输入:grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
输出:11
解释:
一种可能的解决方案是 [右, 右, 顺时针旋转, 右, 下, 下, 下, 下, 逆时针旋转, 右, 下]。
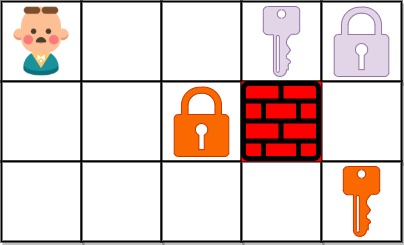
示例 2:
输入:grid = [[0,0,1,1,1,1],
[0,0,0,0,1,1],
[1,1,0,0,0,1],
[1,1,1,0,0,1],
[1,1,1,0,0,1],
[1,1,1,0,0,0]]
输出:9
提示:
2 <= n <= 1000 <= grid[i][j] <= 1- 蛇保证从空单元格开始出发。
使用 BFS 模拟,模拟过程使用二维矩阵存储访问状态,访问状态使用二进制表示:0未访问,1水平访问,2垂直访问,3水平访问+垂直访问
function minimumMoves(grid: number[][]): number {
const n = grid.length;
const dirs = [[0, 0], [0, 1], [1, 0], [1, 1]];
const visited = grid.map(g => g.map(() => 0));
function validate([r1, c1, r2, c2]: number[]) {
const s = r1 === r2 ? 1 : 2;
return grid[r1]?.at(c1) === 0 && grid[r2]?.at(c2) === 0 && (visited[r1][c1] | s) !== visited[r1][c1];
}
for (let step = 0, queue = [[0, 0, 0, 1]]; queue.length; step++) {
const nextQueue = [];
for (const [r1, c1, r2, c2] of queue) {
if (r1 === n - 1 && r2 === n - 1 && c1 === n - 2 && c2 === n - 1) return step;
const s = r1 === r2 ? 1 : 2;
if ((visited[r1][c1] | s) === visited[r1][c1]) continue;
visited[r1][c1] = visited[r1][c1] | s;
const p1 = [r1, c1 + 1, r2, c2 + 1], p2 = [r1 + 1, c1, r2 + 1, c2];
if (validate(p1)) nextQueue.push(p1);
if (validate(p2)) nextQueue.push(p2);
if (!dirs.every(([dr, dc]) => grid[r1 + dr]?.at(c1 + dc) === 0)) continue;
const p3 = [r1, c1, r2 + 1, c2 - 1];
if (r1 === r2 && validate(p3)) nextQueue.push(p3);
const p4 = [r1, c1, r2 - 1, c2 + 1];
if (c1 === c2 && validate(p4)) nextQueue.push(p4);
}
queue = nextQueue;
}
return -1;
};
- 时间复杂度:O(n2)
- 空间复杂度:O(n2)