1、题干
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N
A P L S I I G
Y I R之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入:s = "PAYPALISHIRING", numRows = 3
输出:"PAHNAPLSIIGYIR"
输入:s = "PAYPALISHIRING", numRows = 4
输出:"PINALSIGYAHRPI"
解释:
P I N
A L S I G
Y A H R
P I
示例 3:
输入:s = "A", numRows = 1
输出:"A"
提示:
1 <= s.length <= 1000s由英文字母(小写和大写)、','和'.'组成1 <= numRows <= 1000
2、解法1-逐行计算
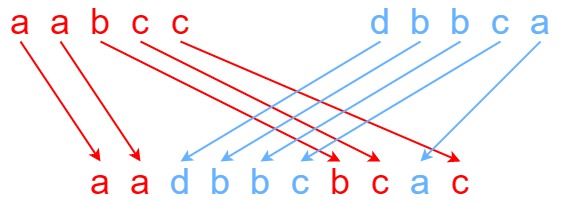
字符按 Z 字形排列后可以分割成多个竖列加斜列字符串,每串长度为 N = 2 * numRows - 2;可以按行计算结果字符串,不处于斜列上的字符其下标计算公式为 i + j * N,其中 i、j 分别为行列号,斜列上的字符下标计算公式为 j * N + N - i,逐行累加所有字符即可
3、代码
var convert = function (s, numRows) {
if (numRows === 1) return s;
const N = 2 * numRows - 2;
const col = Math.ceil(s.length / N);
let res = '';
for (let i = 0; i < numRows; i++) {
for (let j = 0; j < col && i + j * N < s.length; j++) {
if (i % (numRows - 1) === 0) res += s[i + j * N];
else res += s[i + j * N] + (s[j * N + N - i] || '');
}
}
return res;
};
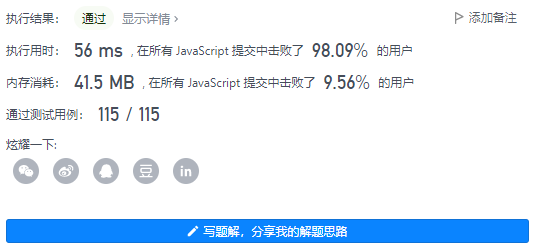
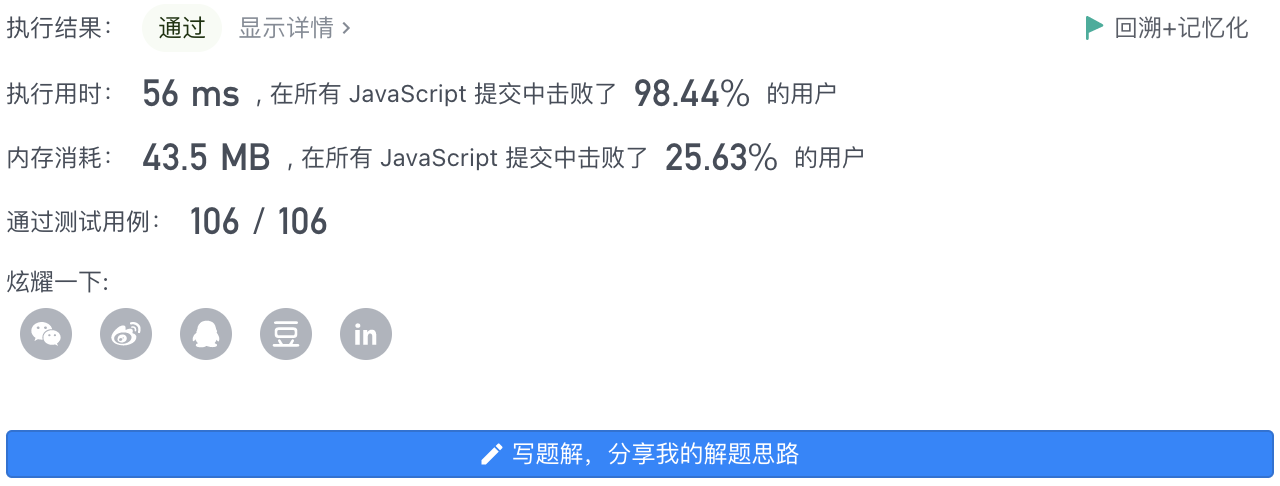
4、执行结果
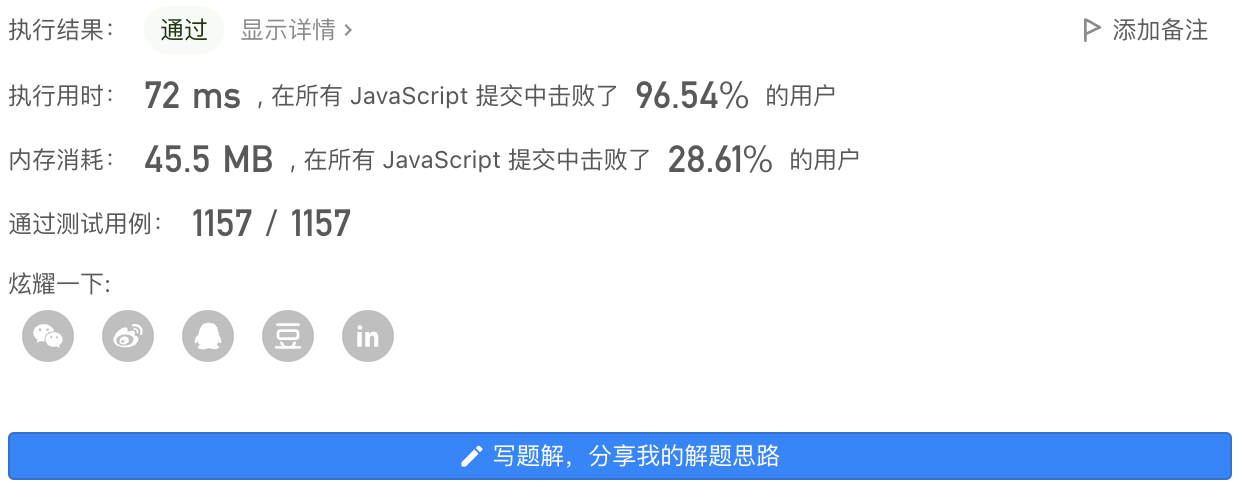
5、解法2-矩阵填充
3年前写的,实际是矩阵模拟的升级版本,思路是遍历字符串并计算当前字符所属行并追加到该行字符串末尾,最后累加所有行的字符串
6、代码
var convert = function (s, numRows) {
if (!s || numRows <= 1 || numRows >= s.length) return s;
const matrix = new Array(numRows).fill('');
const offset = 2 * numRows - 2 || 1;
for (let i = 0; i < s.length; i++) {
let mod = i % offset;
if (mod >= numRows) mod = offset - mod;
matrix[mod] += s[i];
}
return matrix.join('');
};
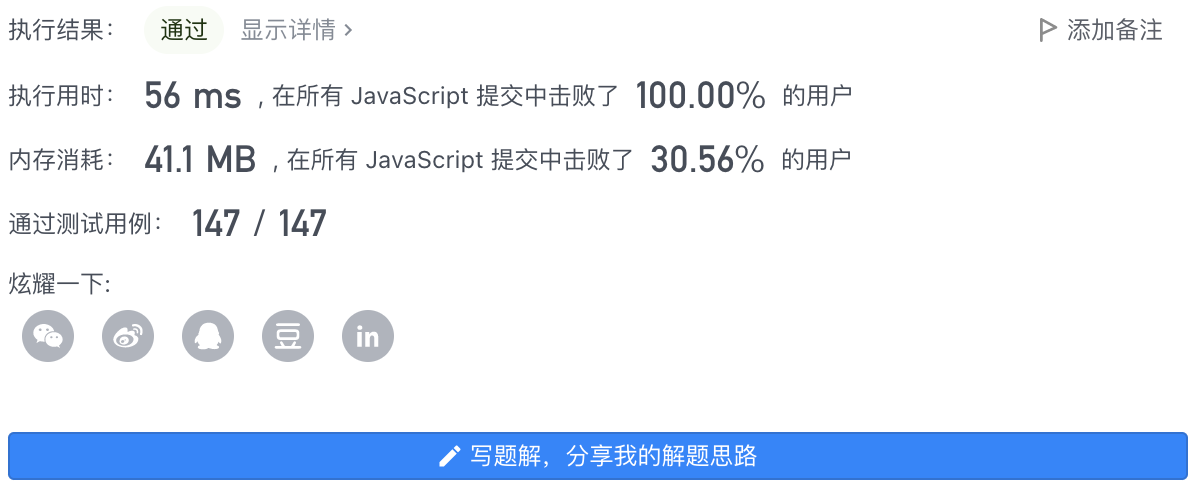
7、执行结果
- 执行用时: 132 ms
- 内存消耗: 37.5 MB