跳到主要内容

3 篇博文 含有标签「单调栈」

查看所有标签

· 阅读需 3 分钟

1、题干​

给你一份工作时间表 hours，上面记录着某一位员工每天的工作小时数。

我们认为当员工一天中的工作小时数大于 8 小时的时候，那么这一天就是「劳累的一天」。

所谓「表现良好的时间段」，意味在这段时间内，「劳累的天数」是严格 大于「不劳累的天数」。

请你返回「表现良好时间段」的最大长度。

 

示例 1：

输入：hours = [9,9,6,0,6,6,9]
输出：3
解释：最长的表现良好时间段是 [9,9,6]。

示例 2：

输入：hours = [6,6,6]
输出：0

 

提示：

  • 1 <= hours.length <= 104
  • 0 <= hours[i] <= 16

2、思路-前缀和+哈希表​

  • 计算 hours 的前缀和数组 sums，当 hours[i] 大于 8 时前缀和 +1 否则 -1
  • 将 sums[i] 与 i 分别作为键值存入哈希表 map；为保证结果时段最大，仅当哈希表中不存在 sums[i] 时才存入该键值对
  • 如果 sums[i] 大于 0，则区间 [0,i] 可能是最长时段
  • 如果 sums[i] 小于等于 0，则区间 [map.get(sums[i] - 1),i) 也可能是最长时段
  • 所有备选时段长度的最大值即所求的最长时段

这题的前缀和在整数范围上具有连续性，所以能用哈希表

3、代码​

function longestWPI(hours: number[]): number {
    const sums = hours.map(() => 0);
    const map = new Map();

    let ans = 0;
    for (let i = 0; i < hours.length; i++) {
        sums[i] = (sums[i - 1] || 0) + (hours[i] > 8 ? 1 : -1);
        if (sums[i] > 0) ans = Math.max(ans, i + 1);
        else {
            if (map.has(sums[i] - 1)) ans = Math.max(ans, i - map.get(sums[i] - 1));
        }

        if (!map.has(sums[i])) map.set(sums[i], i);
    }

    return ans;
};

4、复杂度​

  • 时间复杂度：O(n)O(n)
  • 空间复杂度：O(n)O(n)

5、执行结果​

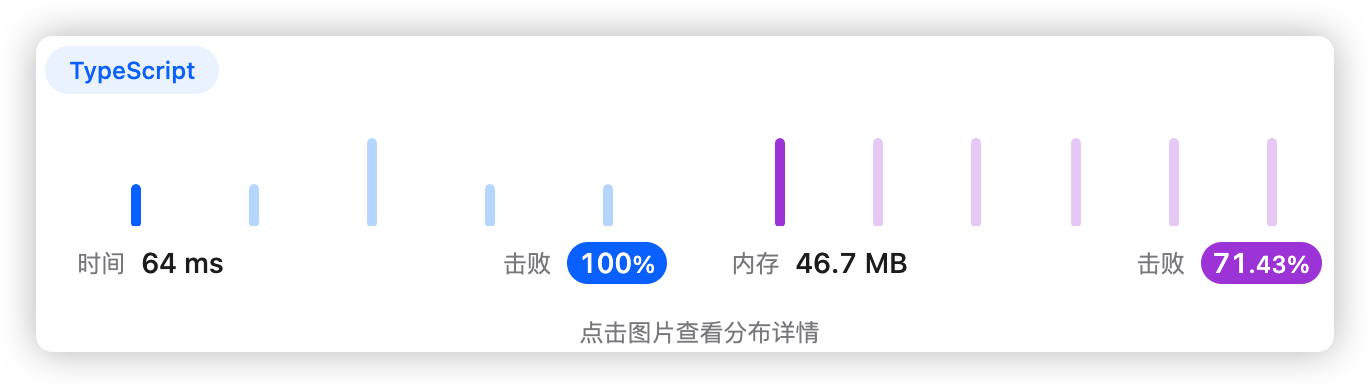
image.png

6、前缀和+栈​

这个思路是我能写出来的吗

function longestWPI(hours: number[]): number {
    const sums = hours.map(() => 0);
    const minStack = [0];

    let ans = 0;
    for (let i = 0; i < hours.length; i++) {
        sums[i] = (sums[i - 1] || 0) + (hours[i] > 8 ? 1 : -1);
        if (sums[i] > 0) ans = Math.max(ans, i + 1);
        if (sums[i] < sums[minStack.at(-1)]) minStack.push(i);
    }

    for (let i = hours.length - 1; i > -1; i--) {
        while (sums[minStack.at(-1)] < sums[i]) {
            const l = minStack.pop();
            ans = Math.max(ans, i - l);
        }
    }

    return ans;
};

· 阅读需 2 分钟

1、题干​

给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。

由于答案可能很大，因此 返回答案模 10^9 + 7 。

 

示例 1：

输入：arr = [3,1,2,4]
输出：17
解释：
子数组为 [3]，[1]，[2]，[4]，[3,1]，[1,2]，[2,4]，[3,1,2]，[1,2,4]，[3,1,2,4]。 
最小值为 3，1，2，4，1，1，2，1，1，1，和为 17。

示例 2：

输入：arr = [11,81,94,43,3]
输出：444

 

提示：

  • 1 <= arr.length <= 3 * 104
  • 1 <= arr[i] <= 3 * 104

 

解题思路​

单调栈，写得有点费力

代码​

function sumSubarrayMins(arr: number[]): number {
  let res = 0;

  function dfs(c: number) {
    const n = arr[c];
    let [mins, preSum] = c < arr.length - 1 ? dfs(c + 1) : [[], 0];

    let count = 1;
    while (mins.at(-1)?.at(0) >= n) {
      const pair = mins.pop();
      count += pair[1];
      preSum -= pair[1] * pair[0];
    }

    mins.push([n, count]);
    preSum = (preSum + n * count) % (1e9 + 7);
    res = (res + preSum) % (1e9 + 7);

    return [mins, preSum];
  }

  dfs(0);

  return res;
}

· 阅读需 7 分钟

1、题干​

你正在参加一个多角色游戏，每个角色都有两个主要属性：攻击 和 防御 。给你一个二维整数数组 properties ，其中 properties[i] = [attacki, defensei] 表示游戏中第 i 个角色的属性。

如果存在一个其他角色的攻击和防御等级 都严格高于 该角色的攻击和防御等级，则认为该角色为 弱角色 。更正式地，如果认为角色 i 弱于 存在的另一个角色 j ，那么 attackj > attacki 且 defensej > defensei 。

返回 弱角色 的数量。

 

示例 1：

输入：properties = [[5,5],[6,3],[3,6]]
输出：0
解释：不存在攻击和防御都严格高于其他角色的角色。

示例 2：

输入：properties = [[2,2],[3,3]]
输出：1
解释：第一个角色是弱角色，因为第二个角色的攻击和防御严格大于该角色。

示例 3：

输入：properties = [[1,5],[10,4],[4,3]]
输出：1
解释：第三个角色是弱角色，因为第二个角色的攻击和防御严格大于该角色。

 

提示：

  • 2 <= properties.length <= 105
  • properties[i].length == 2
  • 1 <= attacki, defensei <= 105

没想到官解那么巧妙的解法，提供一个普通思路。。。

1a709d284924ca5858f365c4e6f6f112.gif


2、解法1​

方便起见将角色属性数组长度 properties.length 记为 nn。


总体思路

  • 先升序排序：对属性数组 properties 按攻击力升序排序
  • 再查找强角色：假设攻击力没有相同值，对于任意角色 i 如果能在区间 [i+1,n−1][i+1, n-1] 内找到一个防御力更大的角色 j，就说明 i 是一个弱角色
  • 预统计区间内最大防御力，加速查找：问题是在区间 [i+1,n−1][i+1, n-1] 内找一个比较大的值需要遍历，时间复杂度不允许，因此可以先统计区间内的最大值，在查找的时候直接使用最大值进行比较即可

大体步骤

  • 先对属性数组 properties 按攻击力升序排序
  • 创建数组 maxDefs 用于记录区间最大防御力，对于任意元素 maxDefs[i] 表示区间 [i,n−1][i, n-1] 内的最大防御力
    • 这里需要倒序遍历 properties，对于任意索引 i，maxDefs[i] 取当前防御力 properties[i][1] 与后续区间最大防御力 maxDefs[i + 1] 中的最大值
    • 最后 maxDefs 会形成一个单调递减的数列
  • 最后顺序遍历 properties ，对于任意角色属性 properties[i]，如果能在区间 [i+1,n−1][i+1, n-1] 找到一个攻击力防御力都更大的角色属性 properties[j]，即 properties[i][0] < properties[j][0] && properties[i][1] < maxDefs[j]，则说明这是一个弱角色
    • 注意这里需要跳过攻击力相同的角色

3、代码​

var numberOfWeakCharacters = function (properties) {
    properties.sort((a, b) => a[0] - b[0]);

    const n = properties.length, maxDefs = new Array(n).fill(0);
    for (let i = n - 1; i > -1; i--) {
        maxDefs[i] = Math.max(maxDefs[i + 1] || 0, properties[i][1]);
    }

    let count = 0;
    for (let i = 0; i < n - 1; i++) {
        let j = i + 1;
        // 跳过攻击力相同的角色
        while (j < n && properties[i][0] === properties[j][0]) j++;
        if (properties[i][1] < maxDefs[j]) count++;
    }

    return count;
};

4、复杂度​

  • 时间复杂度：O(nlogn)O(nlogn) 到 O(n2)O(n^2) 之间
  • 空间复杂度：O(n)O(n)

5、执行结果​

  • 执行用时: 344 ms，超97%
  • 内存消耗: 75.2 MB，超7%

6、解法1-优化​

问题：跳过攻击力相同的角色是后置的，在查找过程中通过遍历的方式逐一跳过，这里增加了时间复杂度 优化：可以参考官解的排序方式：依然按攻击力升序排序，但是当攻击力相同时按防御力降序排序。这里很巧妙地规避了需要跳过攻击力相同角色的问题，因为攻击力相同时按防御力降序排序，意味着后续区间如果出现更大的防御力必定不属于攻击力相同的角色


7、代码​

var numberOfWeakCharacters = function (properties) {
    properties.sort((a, b) => a[0] === b[0] ? b[1] - a[1] : a[0] - b[0]);

    const n = properties.length, maxDefs = new Array(n).fill(0);
    for (let i = n - 1; i > -1; i--) {
        maxDefs[i] = Math.max(maxDefs[i + 1] || 0, properties[i][1]);
    }

    let count = 0;
    for (let i = 0; i < n - 1; i++) {
        if (properties[i][1] < maxDefs[i + 1]) count++;
    }

    return count;
};

8、复杂度​

  • 时间复杂度：O(nlogn)O(nlogn)
  • 空间复杂度：O(n)O(n)

9、执行结果​

  • 执行用时: 336 ms，超97%
  • 内存消耗: 74.8 MB，超7%

如果把优化后的代码调整为按攻击力降序排序或者按倒序遍历查找弱角色，就跟官解一样了，记录区间最大值不再需要数组，只需要一个变量，空间复杂度可以降到 O(1)O(1)，时间复杂度相同。