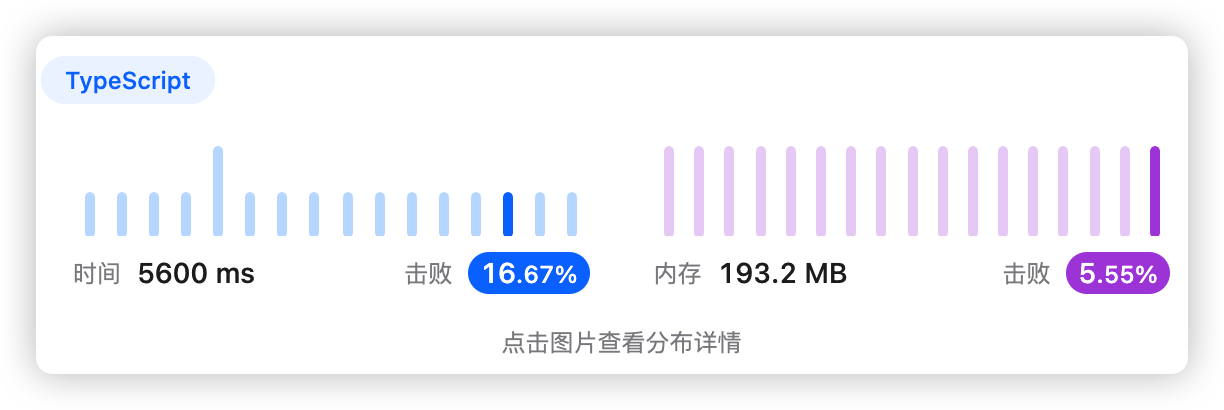
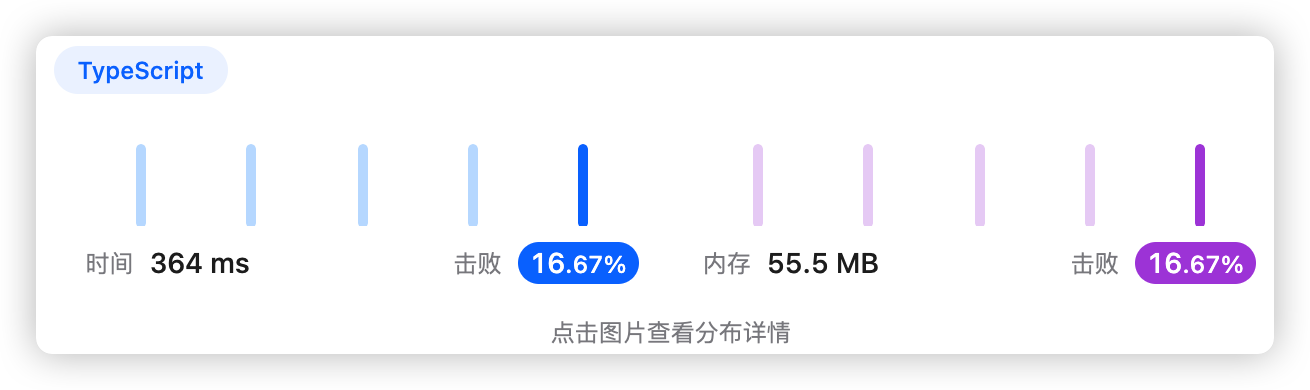
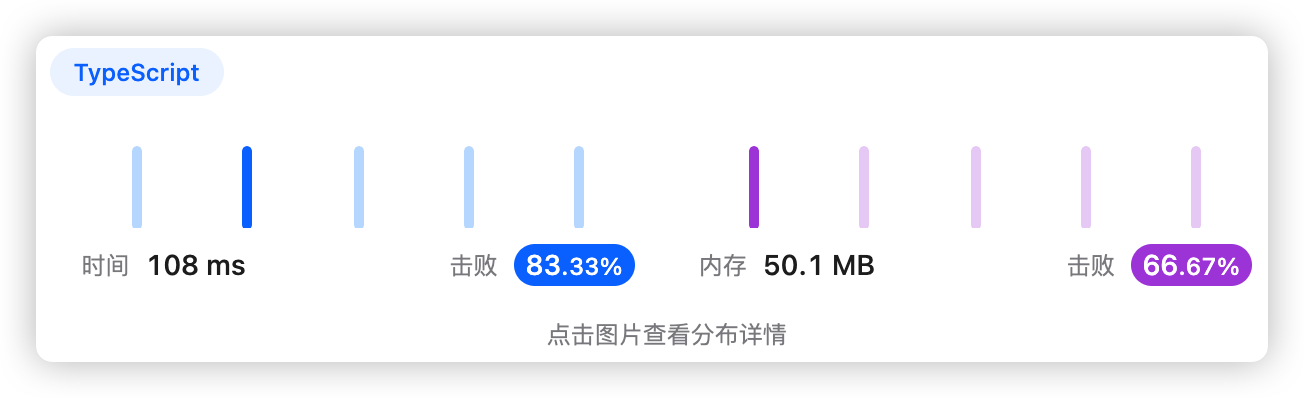
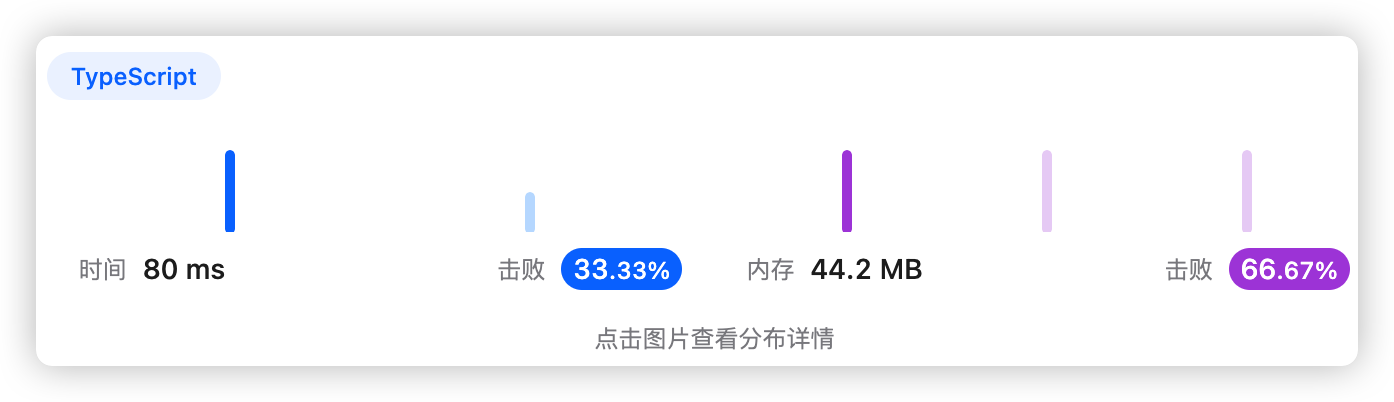
你将会得到一份单词表 words,一个字母表 letters (可能会有重复字母),以及每个字母对应的得分情况表 score。
请你帮忙计算玩家在单词拼写游戏中所能获得的「最高得分」:能够由 letters 里的字母拼写出的 任意 属于 words 单词子集中,分数最高的单词集合的得分。
单词拼写游戏的规则概述如下:
- 玩家需要用字母表
letters 里的字母来拼写单词表 words 中的单词。 - 可以只使用字母表
letters 中的部分字母,但是每个字母最多被使用一次。 - 单词表
words 中每个单词只能计分(使用)一次。 - 根据字母得分情况表
score,字母 'a', 'b', 'c', ... , 'z' 对应的得分分别为 score[0], score[1], ..., score[25]。 - 本场游戏的「得分」是指:玩家所拼写出的单词集合里包含的所有字母的得分之和。
示例 1:
输入:words = ["dog","cat","dad","good"], letters = ["a","a","c","d","d","d","g","o","o"], score = [1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0]
输出:23
解释:
字母得分为 a=1, c=9, d=5, g=3, o=2
使用给定的字母表 letters,我们可以拼写单词 "dad" (5+1+5)和 "good" (3+2+2+5),得分为 23 。
而单词 "dad" 和 "dog" 只能得到 21 分。
示例 2:
输入:words = ["xxxz","ax","bx","cx"], letters = ["z","a","b","c","x","x","x"], score = [4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10]
输出:27
解释:
字母得分为 a=4, b=4, c=4, x=5, z=10
使用给定的字母表 letters,我们可以组成单词 "ax" (4+5), "bx" (4+5) 和 "cx" (4+5) ,总得分为 27 。
单词 "xxxz" 的得分仅为 25 。
示例 3:
输入:words = ["leetcode"], letters = ["l","e","t","c","o","d"], score = [0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0]
输出:0
解释:
字母 "e" 在字母表 letters 中只出现了一次,所以无法组成单词表 words 中的单词。
提示:
1 <= words.length <= 141 <= words[i].length <= 151 <= letters.length <= 100letters[i].length == 1score.length == 260 <= score[i] <= 10words[i] 和 letters[i] 只包含小写的英文字母。
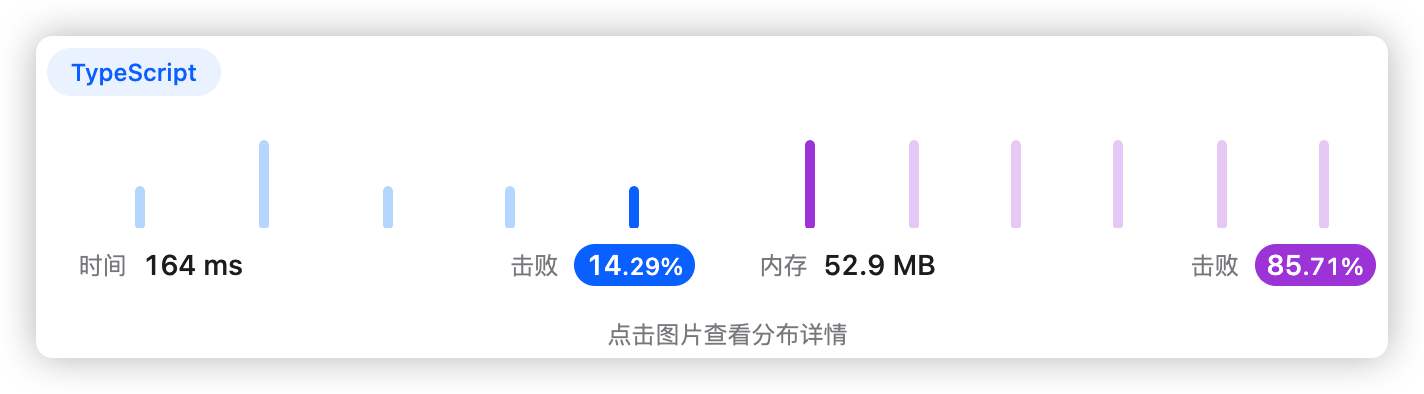
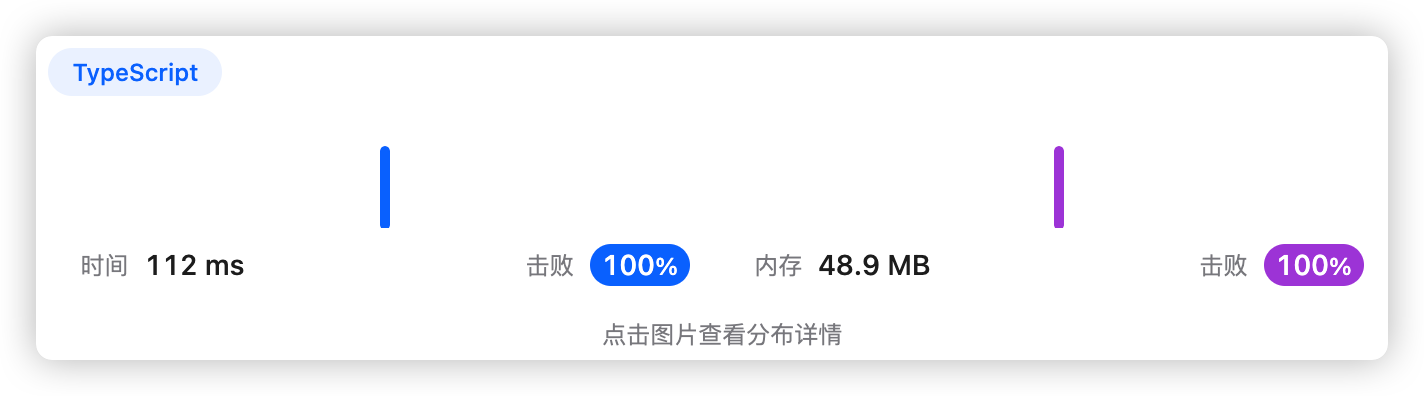
回溯,枚举所有情况计算最高得分。未优化,存在重复计算,效率不高。
function maxScoreWords(words: string[], letters: string[], score: number[]): number {
const wordScore = new Array(words.length).fill(0);
for (let i = 0; i < words.length; i++) {
for (let j = 0; j < words[i].length; j++) {
wordScore[i] += score[words[i][j].charCodeAt(0) - 97];
}
}
const letterDict = new Array(26).fill(0);
for (let i = 0; i < letters.length; i++) {
letterDict[letters[i].charCodeAt(0) - 97] += 1;
}
let ans = 0;
function dfs(sc: number, visited: Set<number>) {
for (let i = 0; i < words.length; i++) {
if (visited.has(i)) continue;
let valid = true;
for (let j = 0; j < words[i].length; j++) {
const c = words[i][j].charCodeAt(0) - 97;
letterDict[c]--;
if (letterDict[c] < 0) valid = false;
}
if (valid) {
ans = Math.max(ans, sc + wordScore[i]);
visited.add(i);
dfs(sc + wordScore[i], visited);
visited.delete(i);
}
for (let j = 0; j < words[i].length; j++) {
letterDict[words[i][j].charCodeAt(0) - 97]++;
}
}
}
return dfs(0, new Set()), ans;
};