1、题干
给你一个长度为 n 的整数数组 nums ,和一个长度为 m 的整数数组 queries 。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是 nums 中 元素之和小于等于 queries[i] 的 子序列 的 最大 长度 。
子序列 是由一个数组删除某些元素(也可以不删除)但不改变剩余元素顺序得到的一个数组。
示例 1:
输入:nums = [4,5,2,1], queries = [3,10,21]
输出:[2,3,4]
解释:queries 对应的 answer 如下:
- 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ,所以 answer[0] = 2 。
- 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ,所以 answer[1] = 3 。
- 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ,所以 answer[2] = 4 。
示例 2:
输入:nums = [2,3,4,5], queries = [1]
输出:[0]
解释:空子序列是唯一一个满足元素和小于或等于 1 的子序列,所以 answer[0] = 0 。
提示:
n == nums.lengthm == queries.length1 <= n, m <= 10001 <= nums[i], queries[i] <= 106
2、思路1-暴力
- 对
nums升序排序,求前缀和 - 暴力查找不大于
queries[i]的前缀和数量
3、代码
function answerQueries(nums: number[], queries: number[]): number[] {
nums.sort((a, b) => a - b);
for (let i = 1; i < nums.length; i++) nums[i] += nums[i - 1];
let ans = queries.map(Number);
for (let i = 0; i < queries.length; i++) {
if (nums.at(-1) <= queries[i]) ans[i] = nums.length;
else ans[i] = nums.findIndex((s) => s > queries[i]);
}
return ans;
};
4、复杂度
- 时间复杂度:
- 空间复杂度:
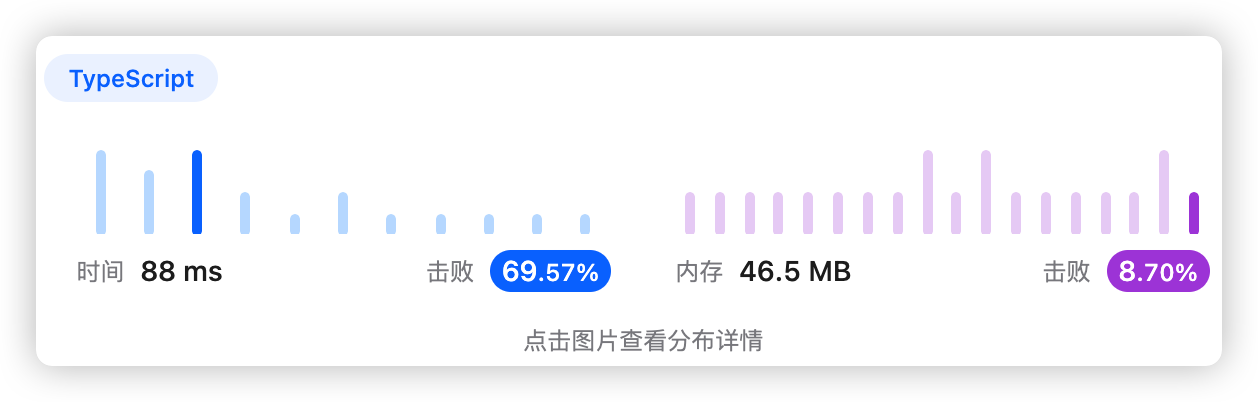
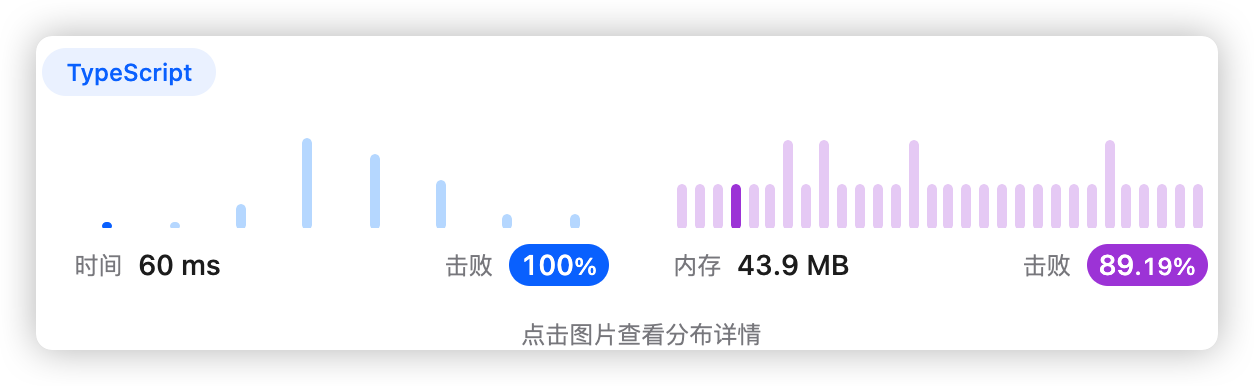
5、执行结果
6、思路2-排序优化
在思路1的基础上进行优化,如果 queries 是升序数组,那么查找子序列就不用每次都从头到尾遍历前缀和数组,可以从上一个找到的前缀和下标开始往后查找,查找过程复杂度从 降到
7、代码
function answerQueries(nums: number[], queries: number[]): number[] {
nums.sort((a, b) => a - b);
for (let i = 1; i < nums.length; i++) nums[i] += nums[i - 1];
const qs = queries.map((n, i) => [n, i]).sort((a, b) => a[0] - b[0]);
let ans = queries.map(Number);
for (let i = 0, j = 0; i < qs.length; i++) {
if (nums.at(-1) <= qs[i][0]) {
ans[qs[i][1]] = nums.length;
continue;
}
while (nums[j] <= qs[i][0]) j++;
ans[qs[i][1]] = j;
}
return ans;
};
8、复杂度
- 时间复杂度:
- 空间复杂度:
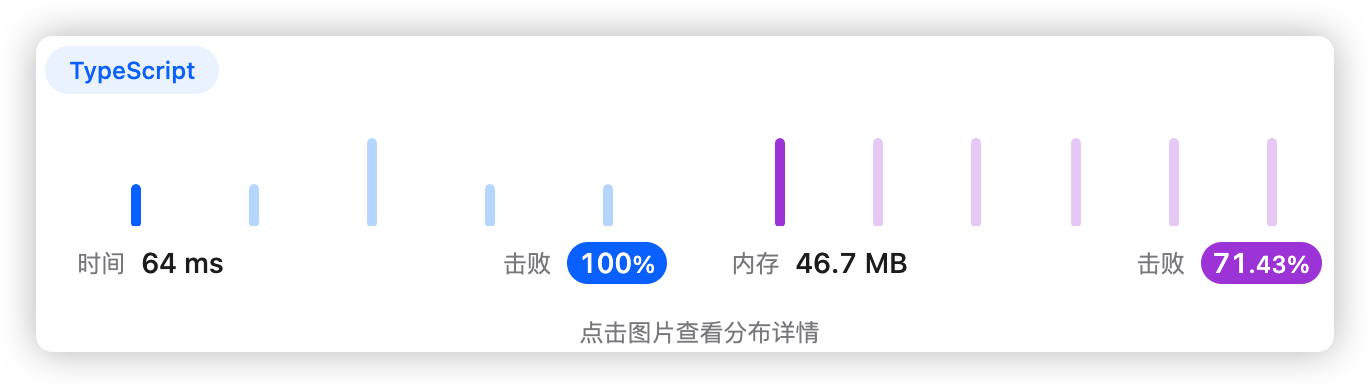
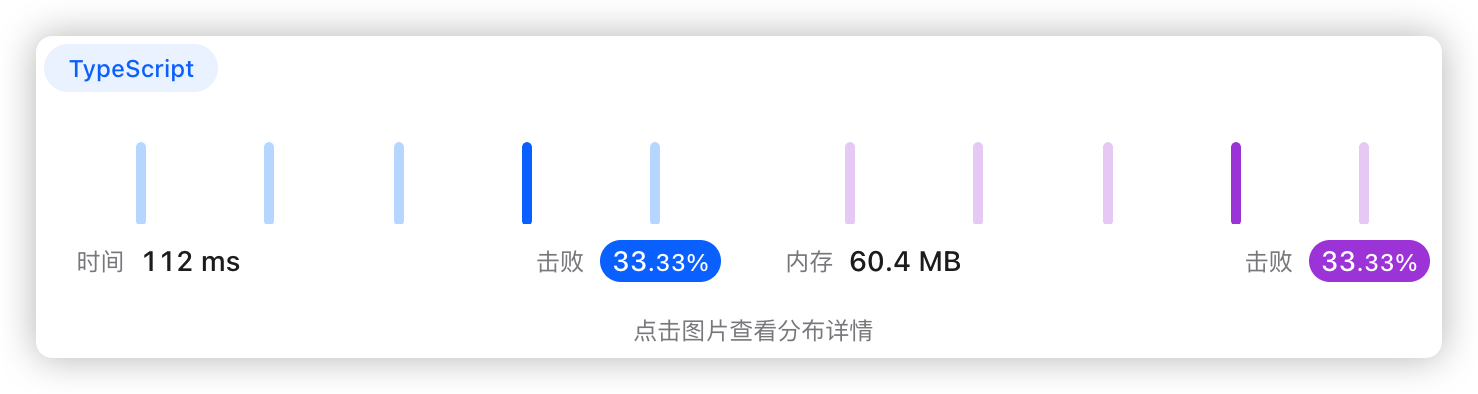
9、执行结果