跳到主要内容

1630.等差子数组

· 阅读需 4 分钟

1、题干​

如果一个数列由至少两个元素组成，且每两个连续元素之间的差值都相同，那么这个序列就是 等差数列 。更正式地，数列 s 是等差数列，只需要满足：对于每个有效的 i ， s[i+1] - s[i] == s[1] - s[0] 都成立。

例如，下面这些都是 等差数列 ：

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

下面的数列 不是等差数列 ：

1, 1, 2, 5, 7

给你一个由 n 个整数组成的数组 nums，和两个由 m 个整数组成的数组 l 和 r，后两个数组表示 m 组范围查询，其中第 i 个查询对应范围 [l[i], r[i]] 。所有数组的下标都是 从 0 开始 的。

返回 boolean 元素构成的答案列表 answer 。如果子数组 nums[l[i]], nums[l[i]+1], ... , nums[r[i]] 可以 重新排列 形成 等差数列 ，answer[i] 的值就是 true；否则answer[i] 的值就是 false 。

 

示例 1：

输入：nums = [4,6,5,9,3,7], l = [0,0,2], r = [2,3,5]
输出：[true,false,true]
解释：
第 0 个查询，对应子数组 [4,6,5] 。可以重新排列为等差数列 [6,5,4] 。
第 1 个查询，对应子数组 [4,6,5,9] 。无法重新排列形成等差数列。
第 2 个查询，对应子数组 [5,9,3,7] 。可以重新排列为等差数列 [3,5,7,9] 。

示例 2：

输入：nums = [-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10], l = [0,1,6,4,8,7], r = [4,4,9,7,9,10]
输出：[false,true,false,false,true,true]

 

提示：

  • n == nums.length
  • m == l.length
  • m == r.length
  • 2 <= n <= 500
  • 1 <= m <= 500
  • 0 <= l[i] < r[i] < n
  • -105 <= nums[i] <= 105

2、思路1​

模拟+计数排序

3、代码​

function checkArithmeticSubarrays(nums: number[], l: number[], r: number[]): boolean[] {
    const ans = new Array(l.length).fill(true);

    for (let i = 0; i < l.length; i++) {
        const len = r[i] - l[i] + 1;
        if (len < 3) continue;

        let min = 1e5, max = -1e5;
        for (let j = l[i]; j <= r[i]; j++) {
            min = Math.min(nums[j], min);
            max = Math.max(nums[j], max);
        }

        if (min === max) continue;

        const d = (max - min) / (len - 1);
        const buckt = new Array(len).fill(0);

        for (let j = l[i]; j <= r[i]; j++) {
            const m = (nums[j] - min) % d;
            const bi = (nums[j] - min) / d;
            if (m || buckt[bi]) {
                ans[i] = false;
                break;
            }
            buckt[bi] = 1;
        }
    }

    return ans;
};

4、复杂度​

  • 时间复杂度：O(n2)O(n^2)
  • 空间复杂度：O(n)O(n)

5、执行结果​

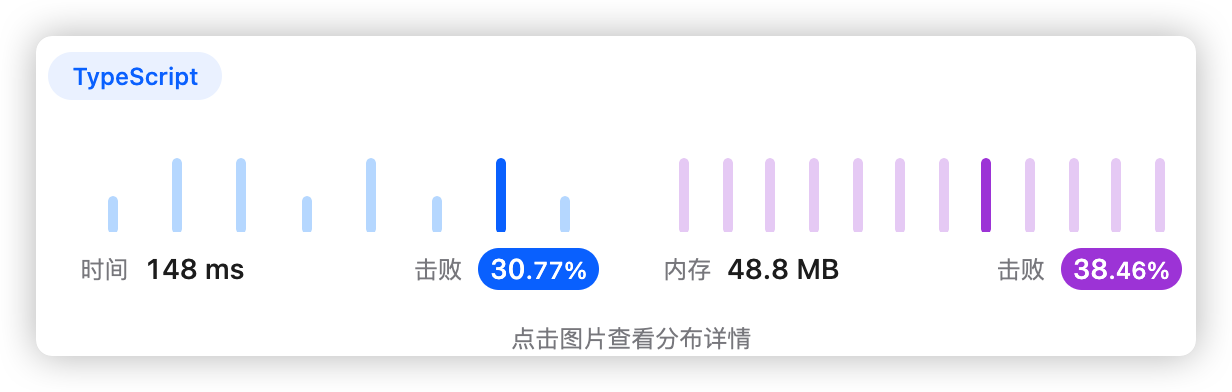
image.png

6、思路2​

模拟+排序API

7、代码​

function checkArithmeticSubarrays(nums: number[], l: number[], r: number[]): boolean[] {
    const ans = l.map(() => true);

    for (let i = 0; i < l.length; i++) {
        if (r[i] - l[i] < 2) continue;
        const arr = nums.slice(l[i], r[i] + 1).sort((a, b) => a - b);

        const d = arr[1] - arr[0];
        for (let j = 2; j < arr.length; j++) {
            if (arr[j] - arr[j - 1] !== d) {
                ans[i] = false;
                break;
            }
        }
    }

    return ans;
};

8、复杂度​

  • 时间复杂度：O(n2log⁡n)O(n^2 \log{n})
  • 空间复杂度：O(n)O(n)

9、执行结果​

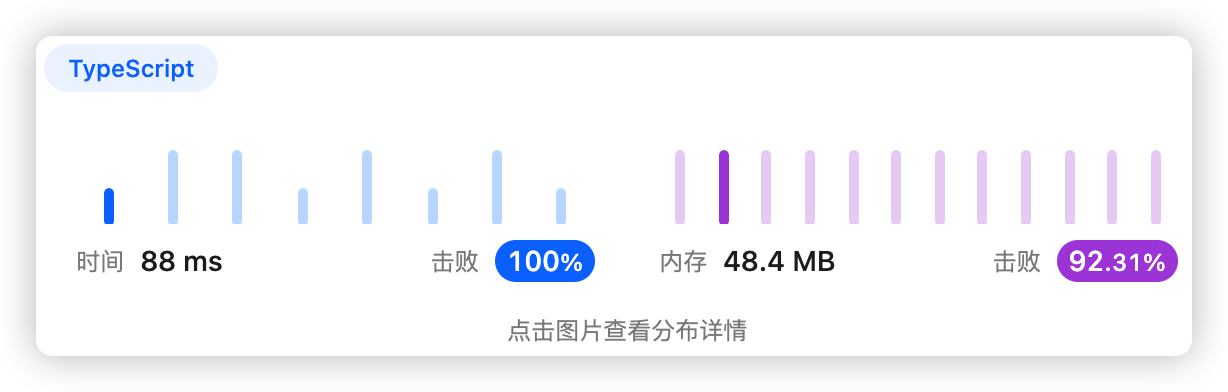
image.png