跳到主要内容

2596.检查骑士巡视方案

· 阅读需 3 分钟

1、题干​

骑士在一张 n x n 的棋盘上巡视。在 有效 的巡视方案中，骑士会从棋盘的 左上角 出发，并且访问棋盘上的每个格子 恰好一次 。

给你一个 n x n 的整数矩阵 grid ，由范围 [0, n * n - 1] 内的不同整数组成，其中 grid[row][col] 表示单元格 (row, col) 是骑士访问的第 grid[row][col] 个单元格。骑士的行动是从下标 0 开始的。

如果 grid 表示了骑士的有效巡视方案，返回 true；否则返回 false。

注意，骑士行动时可以垂直移动两个格子且水平移动一个格子，或水平移动两个格子且垂直移动一个格子。下图展示了骑士从某个格子出发可能的八种行动路线。

 

示例 1：

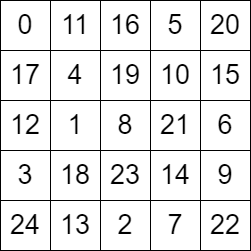
输入：grid = [[0,11,16,5,20],[17,4,19,10,15],[12,1,8,21,6],[3,18,23,14,9],[24,13,2,7,22]]
输出：true
解释：grid 如上图所示，可以证明这是一个有效的巡视方案。

示例 2：

输入：grid = [[0,3,6],[5,8,1],[2,7,4]]
输出：false
解释：grid 如上图所示，考虑到骑士第 7 次行动后的位置，第 8 次行动是无效的。

 

提示：

  • n == grid.length == grid[i].length
  • 3 <= n <= 7
  • 0 <= grid[row][col] < n * n
  • grid 中的所有整数 互不相同

2、思路​

从左上角开始 DFS 遍历，如果能完成遍历则说明巡视方案有效

3、代码​

function checkValidGrid(grid: number[][]): boolean {
    let vis = 0;
    const dirs = [[-2, -1], [2, 1], [-2, 1], [2, -1], [-1, -2], [1, 2], [-1, 2], [1, -2]];
    const t = grid.length * grid[0].length;

    function dfs(r: number, c: number) {
        vis++;
        if (grid[r][c] === t - 1) return;

        for (const [dr, dc] of dirs) {
            if (grid[r + dr]?.at(c + dc) === grid[r][c] + 1) {
                dfs(r + dr, c + dc);
                break;
            }
        }
    }

    dfs(0, 0);

    return vis === t;
};

4、复杂度​

  • 时间复杂度： O(n2)O(n^2)
  • 空间复杂度： O(n2)O(n^2)

5、执行结果​

image.png