1、题干
给你两个非负整数数组 rowSum 和 colSum ,其中 rowSum[i] 是二维矩阵中第 i 行元素的和, colSum[j] 是第 j 列元素的和。换言之你不知道矩阵里的每个元素,但是你知道每一行和每一列的和。
请找到大小为 rowSum.length x colSum.length 的任意 非负整数 矩阵,且该矩阵满足 rowSum 和 colSum 的要求。
请你返回任意一个满足题目要求的二维矩阵,题目保证存在 至少一个 可行矩阵。
示例 1:
输入:rowSum = [3,8], colSum = [4,7]
输出:[[3,0],
[1,7]]
解释:
第 0 行:3 + 0 = 3 == rowSum[0]
第 1 行:1 + 7 = 8 == rowSum[1]
第 0 列:3 + 1 = 4 == colSum[0]
第 1 列:0 + 7 = 7 == colSum[1]
行和列的和都满足题目要求,且所有矩阵元素都是非负的。
另一个可行的矩阵为:[[1,2],
[3,5]]
示例 2:
输入:rowSum = [5,7,10], colSum = [8,6,8]
输出:[[0,5,0],
[6,1,0],
[2,0,8]]
示例 3:
输入:rowSum = [14,9], colSum = [6,9,8]
输出:[[0,9,5],
[6,0,3]]
示例 4:
输入:rowSum = [1,0], colSum = [1]
输出:[[1],
[0]]
示例 5:
输入:rowSum = [0], colSum = [0]
输出:[[0]]
提示:
1 <= rowSum.length, colSum.length <= 5000 <= rowSum[i], colSum[i] <= 108sum(rowSum) == sum(colSum)
以为是个回溯,没想到是个贪心,磨蹭半天才想到,还不是最优的思路
2、思路1
- 生成元素全为 0 的矩阵
grid,grid[0]初始化为colSum - 遍历所有行的元素(最后一行除外),通过
rowSum[i]的约束将超出的数转移到下一行
3、代码
function restoreMatrix(rowSum: number[], colSum: number[]): number[][] {
const grid = rowSum.map(() => colSum.map(() => 0));
grid[0] = colSum;
for (let i = 0; i < rowSum.length - 1; i++) {
let sum = grid[i].reduce((a, c) => a + c, 0);
for (let j = 0; j < colSum.length && sum > rowSum[i]; j++) {
grid[i + 1][j] = Math.min(sum - rowSum[i], grid[i][j]);
grid[i][j] -= grid[i + 1][j];
sum -= grid[i + 1][j];
}
}
return grid;
};
4、复杂度
- 时间复杂度:
- 空间复杂度:
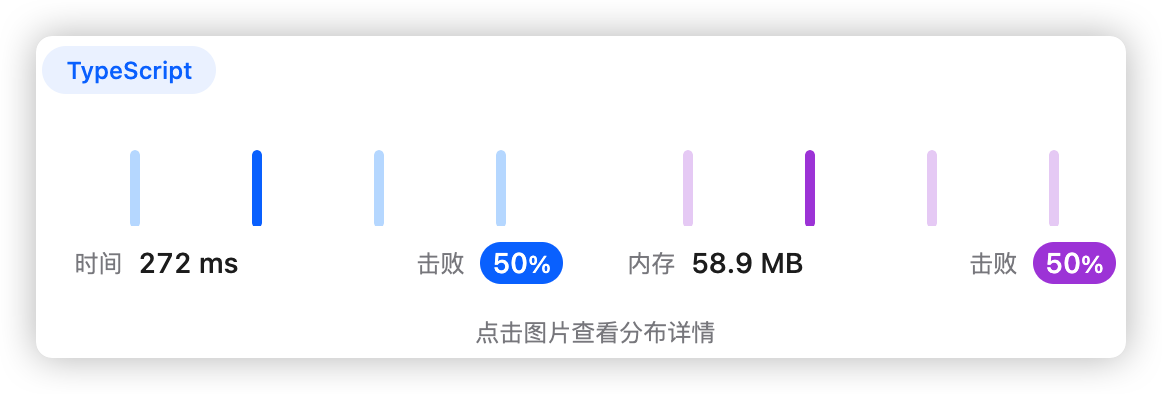
5、执行结果
6、思路2
更直接的贪心,通过 rowSum[i] 与 colSum[j] 直接约束 grid[i][j]
7、代码
function restoreMatrix(rowSum: number[], colSum: number[]): number[][] {
const grid = rowSum.map(() => colSum.map(() => 0));
for (let i = 0; i < rowSum.length; i++) {
for (let j = 0; j < colSum.length; j++) {
grid[i][j] = Math.min(rowSum[i], colSum[j]);
rowSum[i] -= grid[i][j];
colSum[j] -= grid[i][j];
}
}
return grid;
};
8、复杂度
- 时间复杂度:
- 空间复杂度:
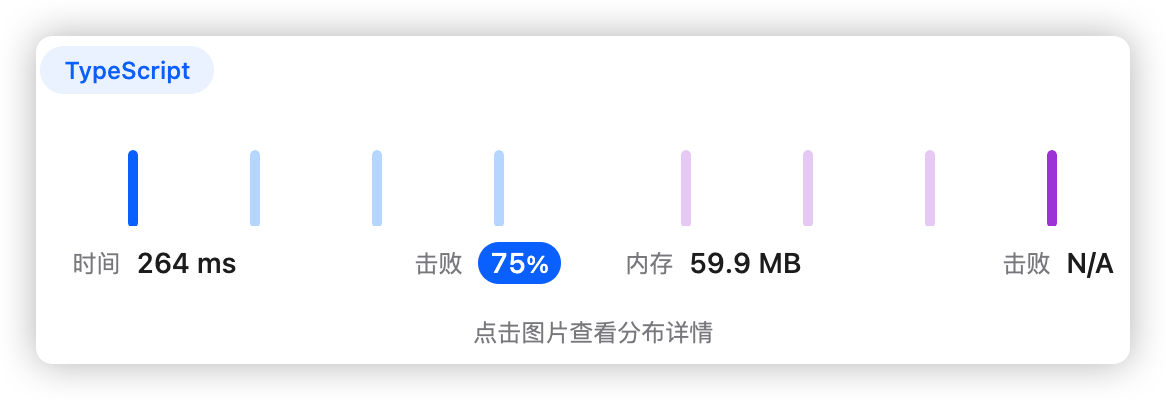
9、执行结果