跳到主要内容

2373.矩阵中的局部最大值

· 阅读需 3 分钟

1、题干​

给你一个大小为 n x n 的整数矩阵 grid 。

生成一个大小为 (n - 2) x (n - 2) 的整数矩阵  maxLocal ，并满足：

  • maxLocal[i][j] 等于 grid 中以 i + 1 行和 j + 1 列为中心的 3 x 3 矩阵中的 最大值 。

换句话说，我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。

返回生成的矩阵。

 

示例 1：

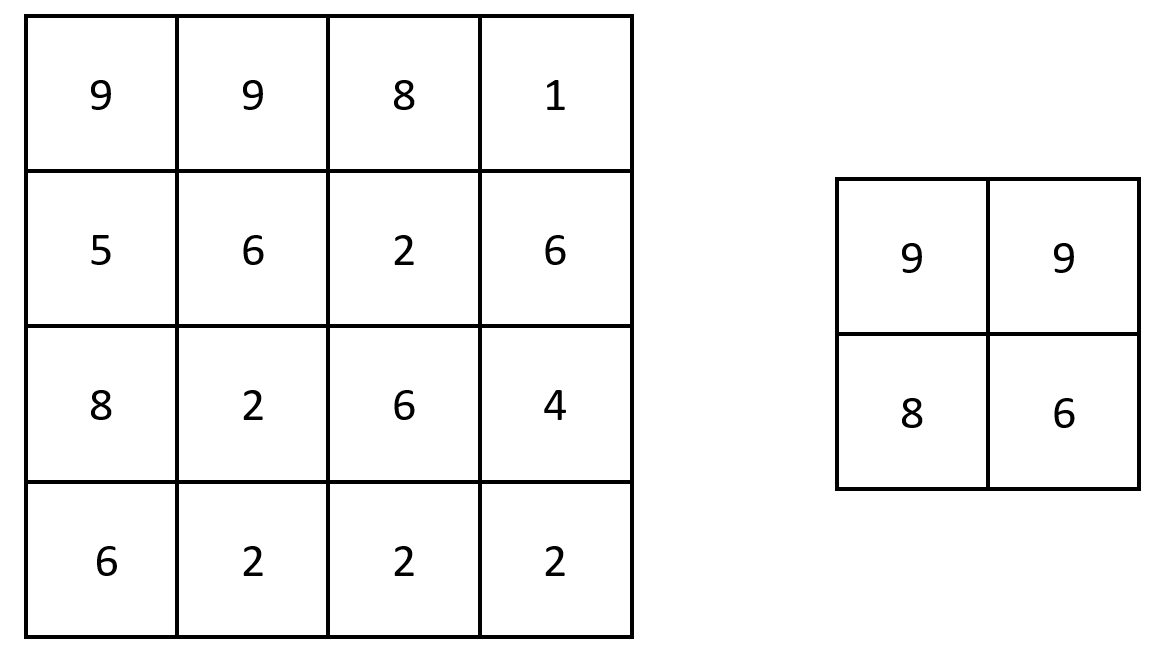
输入：grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
输出：[[9,9],[8,6]]
解释：原矩阵和生成的矩阵如上图所示。
注意，生成的矩阵中，每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。

示例 2：

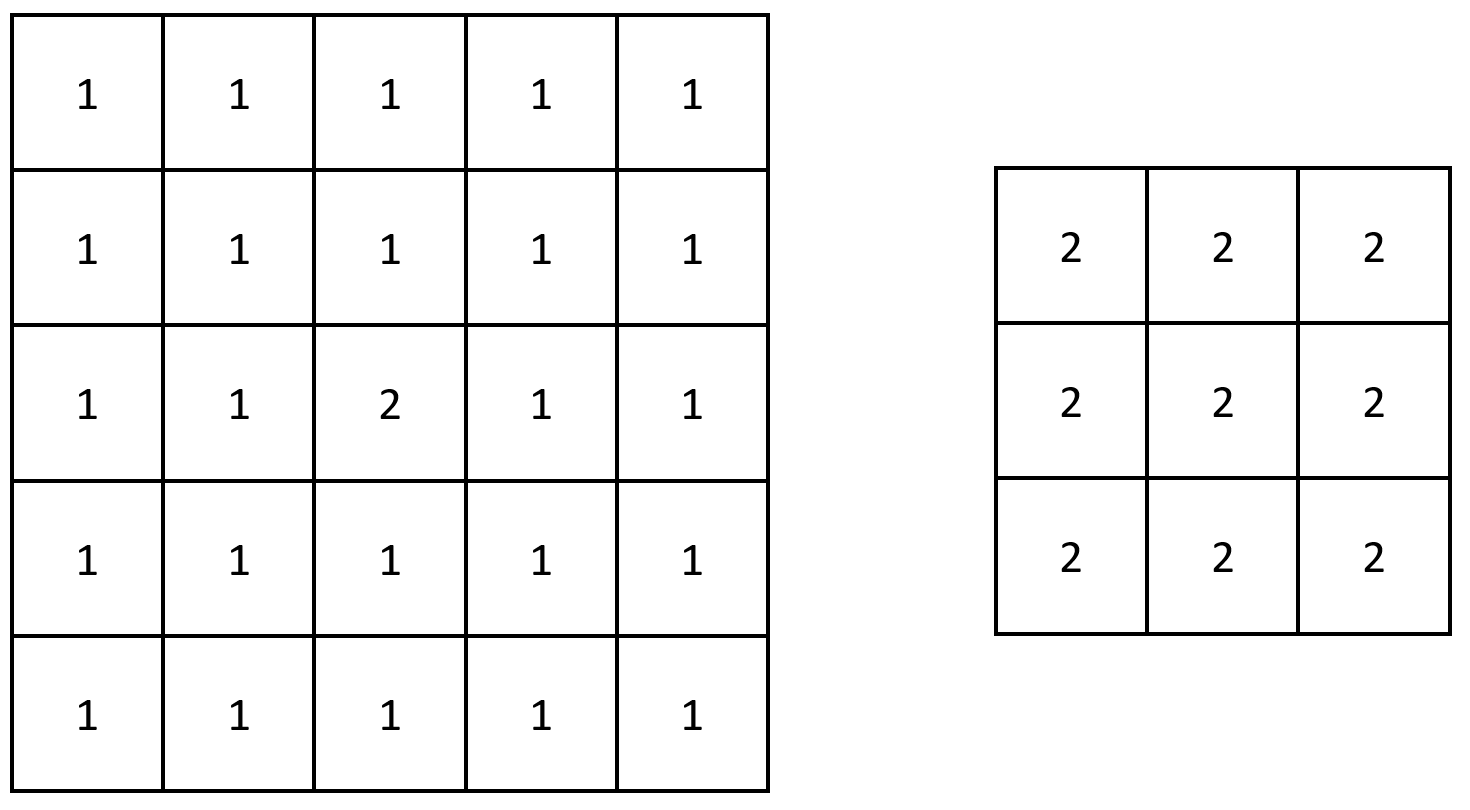
输入：grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
输出：[[2,2,2],[2,2,2],[2,2,2]]
解释：注意，2 包含在 grid 中每个 3 x 3 的矩阵中。

 

提示：

  • n == grid.length == grid[i].length
  • 3 <= n <= 100
  • 1 <= grid[i][j] <= 100

2、思路​

遍历矩阵 [1,n-2] 行列范围内的元素，该元素所在九宫格的最大整数作为最大值存入结果矩阵

3、代码​

function largestLocal(grid: number[][]): number[][] {
    const n = grid.length;
    const dirs = [[1, 0], [-1, 0], [0, 1], [0, -1], [1, -1], [-1, -1], [-1, 1], [1, 1]];
    const ans = Array.from({ length: n - 2 }, () => Array.from({ length: n - 2 }, () => 0));

    for (let i = 1; i < n - 1; i++) {
        for (let j = 1; j < n - 1; j++) {
            ans[i - 1][j - 1] = grid[i][j];
            
            for (let k = 0; k < dirs.length; k++) {
                ans[i - 1][j - 1] = Math.max(ans[i - 1][j - 1], grid[i + dirs[k][0]][j + dirs[k][1]]);
            }
        }
    }

    return ans;
};

4、复杂度​

  • 时间复杂度：O(n2)O(n^2)
  • 空间复杂度：O(1)O(1)

5、执行结果​

image.png