跳到主要内容

1145.二叉树着色游戏

· 阅读需 4 分钟

1、题干​

有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中，给出二叉树的根节点 root，树上总共有 n 个节点，且 n 为奇数，其中每个节点上的值从 1 到 n 各不相同。

最开始时：

  • 「一号」玩家从 [1, n] 中取一个值 x（1 <= x <= n）；
  • 「二号」玩家也从 [1, n] 中取一个值 y（1 <= y <= n）且 y != x。

「一号」玩家给值为 x 的节点染上红色，而「二号」玩家给值为 y 的节点染上蓝色。

之后两位玩家轮流进行操作，「一号」玩家先手。每一回合，玩家选择一个被他染过色的节点，将所选节点一个 未着色 的邻节点（即左右子节点、或父节点）进行染色（「一号」玩家染红色，「二号」玩家染蓝色）。

如果（且仅在此种情况下）当前玩家无法找到这样的节点来染色时，其回合就会被跳过。

若两个玩家都没有可以染色的节点时，游戏结束。着色节点最多的那位玩家获得胜利 ✌️。

现在，假设你是「二号」玩家，根据所给出的输入，假如存在一个 y 值可以确保你赢得这场游戏，则返回 true ；若无法获胜，就请返回 false 。

 

示例 1 ：

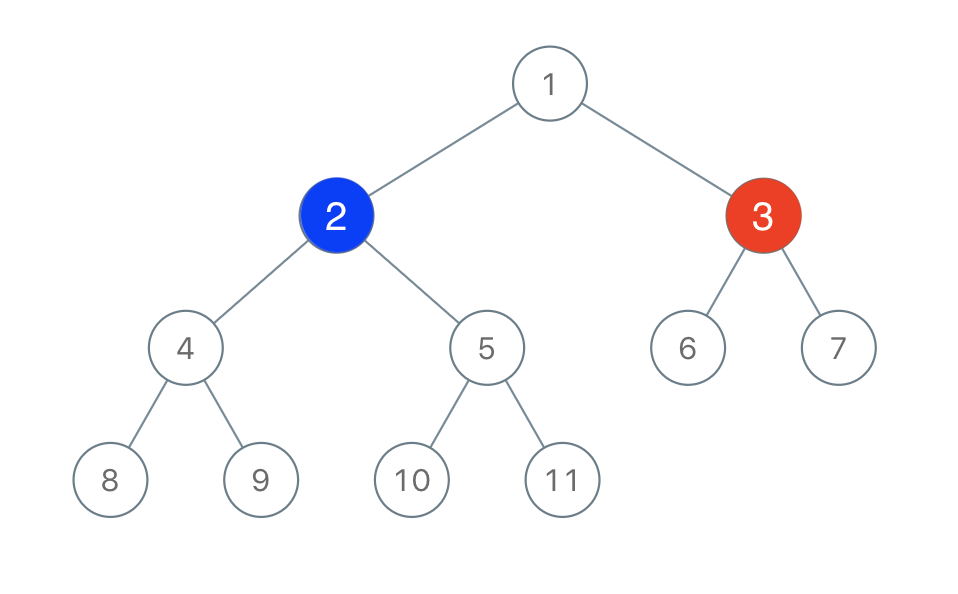
输入：root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
输出：true
解释：第二个玩家可以选择值为 2 的节点。

示例 2 ：

输入：root = [1,2,3], n = 3, x = 1
输出：false

 

提示：

  • 树中节点数目为 n
  • 1 <= x <= n <= 100
  • n 是奇数
  • 1 <= Node.val <= n
  • 树中所有值 互不相同

还好不是博弈论

2、思路​

DFS 求出整棵树的节点总数 c 和节点 x 的左右子树的节点总数 cl 、cr，继而可以求得 x 子树之外的节点总数 c - cl - cr - 1，3者中的最大值如果超过节点总数的一半 c/2，则必定存在必胜值 y

3、代码​

function btreeGameWinningMove(root: TreeNode | null, n: number, x: number): boolean {
    let cl = 0, cr = 0;

    function dfs(node: TreeNode) {
        if (!node) return 0;

        const c1 = dfs(node.left);
        const c2 = dfs(node.right);

        if (node.val === x) cl = c1, cr = c2;

        return c1 + c2 + 1;
    }

    const c = dfs(root);

    return Math.max(c - cl - cr - 1, cl, cr) > c / 2;
};

4、复杂度​

  • 时间复杂度：O(n)O(n)
  • 空间复杂度：O(1)O(1)

5、执行结果​

image.png