2293.极大极小游戏

1、题干

给你一个下标从 0 开始的整数数组 nums ，其长度是 2 的幂。

对 nums 执行下述算法：

1. 设 n 等于 nums 的长度，如果 n == 1 ，终止 算法过程。否则，创建 一个新的整数数组 newNums ，新数组长度为 n / 2 ，下标从 0 开始。
2. 对于满足 0 <= i < n / 2 的每个 偶数 下标 i ，将 newNums[i] 赋值 为 min(nums[2 * i], nums[2 * i + 1]) 。
3. 对于满足 0 <= i < n / 2 的每个 奇数 下标 i ，将 newNums[i] 赋值 为 max(nums[2 * i], nums[2 * i + 1]) 。
4. 用 newNums 替换 nums 。
5. 从步骤 1 开始 重复 整个过程。

执行算法后，返回 nums 中剩下的那个数字。

 

示例 1：

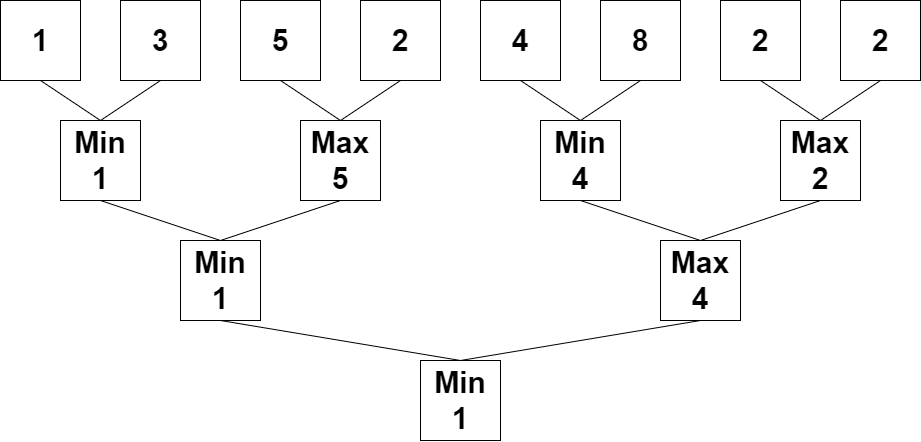
输入：nums = [1,3,5,2,4,8,2,2]
输出：1
解释：重复执行算法会得到下述数组。
第一轮：nums = [1,5,4,2]
第二轮：nums = [1,4]
第三轮：nums = [1]
1 是最后剩下的那个数字，返回 1 。

示例 2：

输入：nums = [3]
输出：3
解释：3 就是最后剩下的数字，返回 3 。

 

提示：

• 1 <= nums.length <= 1024
• 1 <= nums[i] <= 109
• nums.length 是 2 的幂

2、思路

递归模拟，思路和实现比其他方式相对简单点

3、代码

function minMaxGame(nums: number[]): number {
    if (nums.length === 1) return nums[0];

    nums = nums.slice(0, nums.length / 2).map((v, i) => {
        return (i % 2 ? Math.max : Math.min)(nums[2 * i], nums[2 * i + 1]);
    });

    return minMaxGame(nums);
};

4、复杂度

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

5、执行结果