跳到主要内容

1801.积压订单中的订单总数

· 阅读需 7 分钟

1、题干​

给你一个二维整数数组 orders ，其中每个 orders[i] = [pricei, amounti, orderTypei] 表示有 amounti 笔类型为 orderTypei 、价格为 pricei 的订单。

订单类型 orderTypei 可以分为两种：

  • 0 表示这是一批采购订单 buy
  • 1 表示这是一批销售订单 sell

注意，orders[i] 表示一批共计 amounti 笔的独立订单，这些订单的价格和类型相同。对于所有有效的 i ，由 orders[i] 表示的所有订单提交时间均早于 orders[i+1] 表示的所有订单。

存在由未执行订单组成的 积压订单 。积压订单最初是空的。提交订单时，会发生以下情况：

  • 如果该订单是一笔采购订单 buy ，则可以查看积压订单中价格 最低 的销售订单 sell 。如果该销售订单 sell 的价格 低于或等于 当前采购订单 buy 的价格，则匹配并执行这两笔订单，并将销售订单 sell 从积压订单中删除。否则，采购订单 buy 将会添加到积压订单中。
  • 反之亦然，如果该订单是一笔销售订单 sell ，则可以查看积压订单中价格 最高 的采购订单 buy 。如果该采购订单 buy 的价格 高于或等于 当前销售订单 sell 的价格，则匹配并执行这两笔订单，并将采购订单 buy 从积压订单中删除。否则，销售订单 sell 将会添加到积压订单中。

输入所有订单后，返回积压订单中的 订单总数 。由于数字可能很大，所以需要返回对 109 + 7 取余的结果。

 

示例 1：

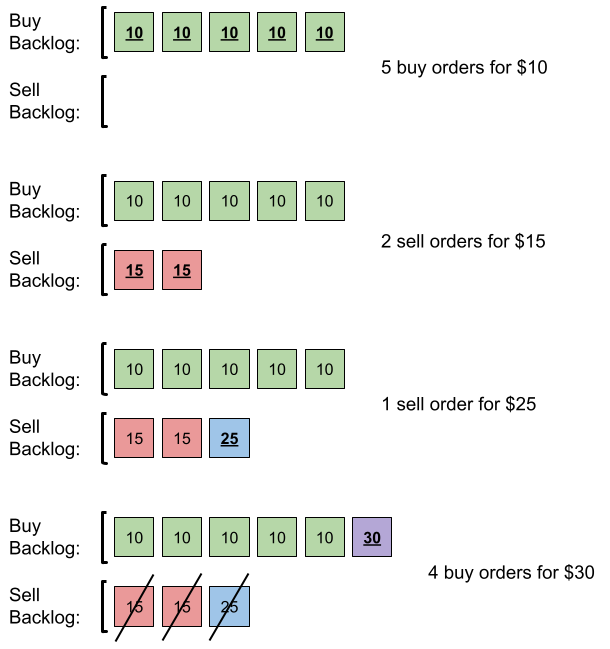
输入：orders = [[10,5,0],[15,2,1],[25,1,1],[30,4,0]]
输出：6
解释：输入订单后会发生下述情况：
- 提交 5 笔采购订单，价格为 10 。没有销售订单，所以这 5 笔订单添加到积压订单中。
- 提交 2 笔销售订单，价格为 15 。没有采购订单的价格大于或等于 15 ，所以这 2 笔订单添加到积压订单中。
- 提交 1 笔销售订单，价格为 25 。没有采购订单的价格大于或等于 25 ，所以这 1 笔订单添加到积压订单中。
- 提交 4 笔采购订单，价格为 30 。前 2 笔采购订单与价格最低（价格为 15）的 2 笔销售订单匹配，从积压订单中删除这 2 笔销售订单。第 3 笔采购订单与价格最低的 1 笔销售订单匹配，销售订单价格为 25 ，从积压订单中删除这 1 笔销售订单。积压订单中不存在更多销售订单，所以第 4 笔采购订单需要添加到积压订单中。
最终，积压订单中有 5 笔价格为 10 的采购订单，和 1 笔价格为 30 的采购订单。所以积压订单中的订单总数为 6 。

示例 2：

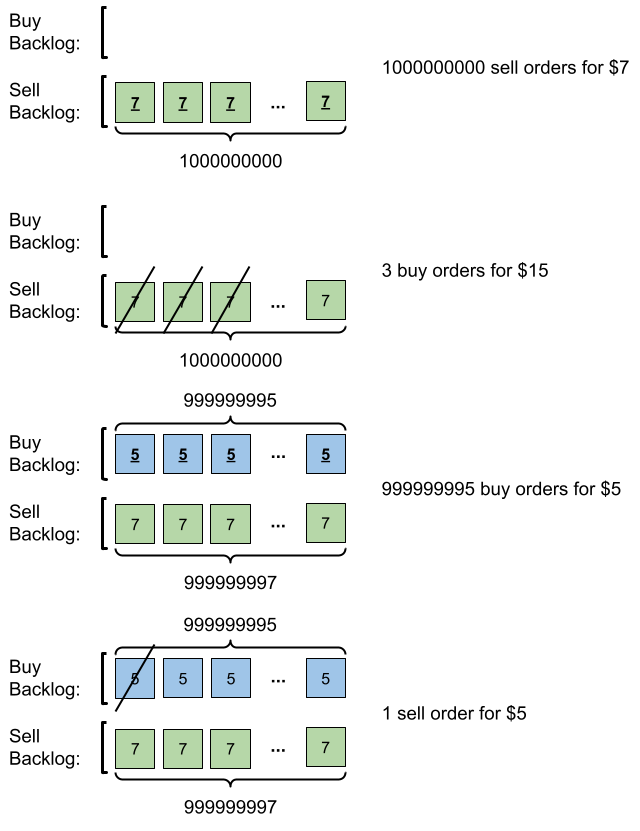
输入：orders = [[7,1000000000,1],[15,3,0],[5,999999995,0],[5,1,1]]
输出：999999984
解释：输入订单后会发生下述情况：
- 提交 109 笔销售订单，价格为 7 。没有采购订单，所以这 109 笔订单添加到积压订单中。
- 提交 3 笔采购订单，价格为 15 。这些采购订单与价格最低（价格为 7 ）的 3 笔销售订单匹配，从积压订单中删除这 3 笔销售订单。
- 提交 999999995 笔采购订单，价格为 5 。销售订单的最低价为 7 ，所以这 999999995 笔订单添加到积压订单中。
- 提交 1 笔销售订单，价格为 5 。这笔销售订单与价格最高（价格为 5 ）的 1 笔采购订单匹配，从积压订单中删除这 1 笔采购订单。
最终，积压订单中有 (1000000000-3) 笔价格为 7 的销售订单，和 (999999995-1) 笔价格为 5 的采购订单。所以积压订单中的订单总数为 1999999991 ，等于 999999984 % (109 + 7) 。

 

提示：

  • 1 <= orders.length <= 105
  • orders[i].length == 3
  • 1 <= pricei, amounti <= 109
  • orderTypei 为 0 或 1

2、思路​

根据题意模拟，使用优先队列存储销售订单和采购订单

3、代码​

function getNumberOfBacklogOrders(orders: number[][]): number {
    const bpq = new PriorityQueue({ compare: (a, b) => b.price - a.price });
    const spq = new PriorityQueue({ compare: (a, b) => a.price - b.price });

    for (let [price, amount, type] of orders) {
        if (type === 0) {
            while (spq.size() && amount > 0) {
                const o = spq.front();
                if (o.price > price) break;
                amount -= o.amount;
                if (amount >= 0) spq.dequeue();
                else o.amount = -amount;
            }

            if (amount > 0) bpq.enqueue({ price, amount });
        } else {
            while (bpq.size() && amount > 0) {
                const o = bpq.front();
                if (o.price < price) break;
                amount -= o.amount;
                if (amount >= 0) bpq.dequeue();
                else o.amount = -amount;
            }

            if (amount > 0) spq.enqueue({ price, amount });
        }
    }

    let ans = 0, M = 1e9 + 7;
    while (bpq.size()) {
        const o = bpq.dequeue();
        ans = (ans + o.amount) % M;
    }

    while (spq.size()) {
        const o = spq.dequeue();
        ans = (ans + o.amount) % M;
    }

    return ans;
};

4、复杂度​

  • 时间复杂度：o(n∗logn)o(n*logn)
  • 空间复杂度：o(n)o(n)

5、执行结果​

image.png