跳到主要内容

864.获取所有钥匙的最短路径

· 阅读需 5 分钟

1、题干​

给定一个二维网格 grid ，其中：

  • '.' 代表一个空房间
  • '#' 代表一堵墙
  • '@' 是起点
  • 小写字母代表钥匙
  • 大写字母代表锁

我们从起点开始出发，一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走，也无法穿过一堵墙。如果途经一个钥匙，我们就把它捡起来。除非我们手里有对应的钥匙，否则无法通过锁。

假设 k 为 钥匙/锁 的个数，且满足 1 <= k <= 6，字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之，每个锁有唯一对应的钥匙，每个钥匙也有唯一对应的锁。另外，代表钥匙和锁的字母互为大小写并按字母顺序排列。

返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙，返回 -1 。

 

示例 1：

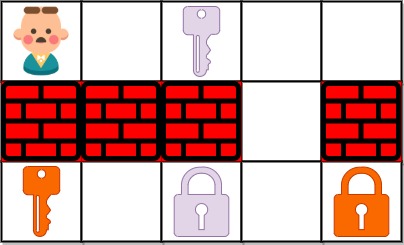
输入：grid = ["@.a..","###.#","b.A.B"]
输出：8
解释：目标是获得所有钥匙，而不是打开所有锁。

示例 2：

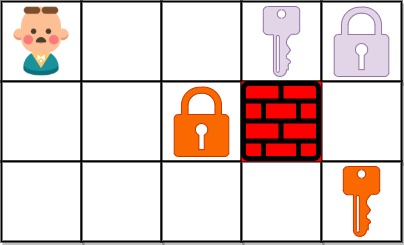
输入：grid = ["@..aA","..B#.","....b"]
输出：6

示例 3:

输入: grid = ["@Aa"]
输出: -1

 

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 30
  • grid[i][j] 只含有 '.', '#', '@', 'a'-'f' 以及 'A'-'F'
  • 钥匙的数目范围是 [1, 6] 
  • 每个钥匙都对应一个 不同 的字母
  • 每个钥匙正好打开一个对应的锁

Problem: 864. 获取所有钥匙的最短路径

2、思路​

写过最长的代码，心态崩了

思路：

  • 回溯，对所有钥匙进行排列组合，得到所有路径（不校验路径是否连通）
  • 遍历所有路径，累计从起点经过所有钥匙需要的步数，结果取最小步数
  • 广搜计算两把钥匙之间的最短路径（需要校验路径是否连通）

3、Code​

function shortestPathAllKeys(grid: string[]): number {
    const m = grid.length, n = grid[0].length;

    const M = 10007;
    const encode = (i: number, j: number) => i * M + j;
    const decode = (d: number) => [(d / M) >> 0, d % M];

    let start = 0;
    const keys: number[] = [];
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] === "@") start = encode(i, j);
            if (grid[i][j] >= "a" && grid[i][j] <= "f") keys.push(encode(i, j));
        }
    }

    // 寻找两把钥匙之间的最短路径
    function bfs(source: number, target: number, visited: Set<number>, foundKeys: Set<string>): number {
        let queue = [source];
        const [ti, tj] = decode(target);

        let step = 1;
        while (queue.length) {
            const nextQueue = new Set<number>();

            for (const q of queue) {
                if (visited.has(q)) continue;
                visited.add(q);

                const [qi, qj] = decode(q);
                const dirs = [[qi, qj + 1], [qi, qj - 1], [qi + 1, qj], [qi - 1, qj],];

                for (const [i, j] of dirs) {
                    if (!grid[i] || !grid[i][j] || grid[i][j] === "#") continue;
                    if (grid[i][j] >= "A" && grid[i][j] <= "F" && !foundKeys.has(grid[i][j].toLowerCase())) continue;
                    if (i === ti && j === tj) return step;

                    nextQueue.add(encode(i, j));
                }
            }

            step++;
            queue = [...nextQueue];
        }

        return 0;
    }

    // 遍历所有路径，累计从起点经过所有钥匙需要的步数，结果取最小步数
    let res = Infinity;
    function calcSteps(path: Set<number>) {
        let step = 0, source = start, foundKeys = new Set<string>();

        for (const p of path) {
            const st = bfs(source, p, new Set(), foundKeys);
            step += st;
            if (!st || step >= res) return;

            const [pi, pj] = decode(p);
            foundKeys.add(grid[pi][pj]);
            source = p;
        }

        if (step < res) res = step;
    }

    // 对钥匙进行排列组合
    function dfs(path: Set<number>) {
        for (const k of keys) {
            if (path.has(k)) continue;
            path.add(k);
            dfs(path);
            if (path.size === keys.length) calcSteps(path);
            path.delete(k);
        }
    }

    dfs(new Set());

    return res === Infinity ? -1 : res;
}

4、复杂度​

  • 时间复杂度：O(k!∗mn)O(k!*mn)
  • 空间复杂度：O(mn)O(mn)

5、执行结果​

image.png