跳到主要内容

1601.最多可达成的换楼请求数目

· 阅读需 5 分钟

1、题干​

我们有 n 栋楼，编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节，部分员工想要换一栋楼居住。

给你一个数组 requests ，其中 requests[i] = [fromi, toi] ，表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。

一开始 所有楼都是满的，所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ，一个员工要离开楼 1 ，一个员工要离开楼 2 ，如果该请求列表可行，应该要有两个员工搬入楼 0 ，一个员工搬入楼 1 ，一个员工搬入楼 2 。

请你从原请求列表中选出若干个请求，使得它们是一个可行的请求列表，并返回所有可行列表中最大请求数目。

 

示例 1：

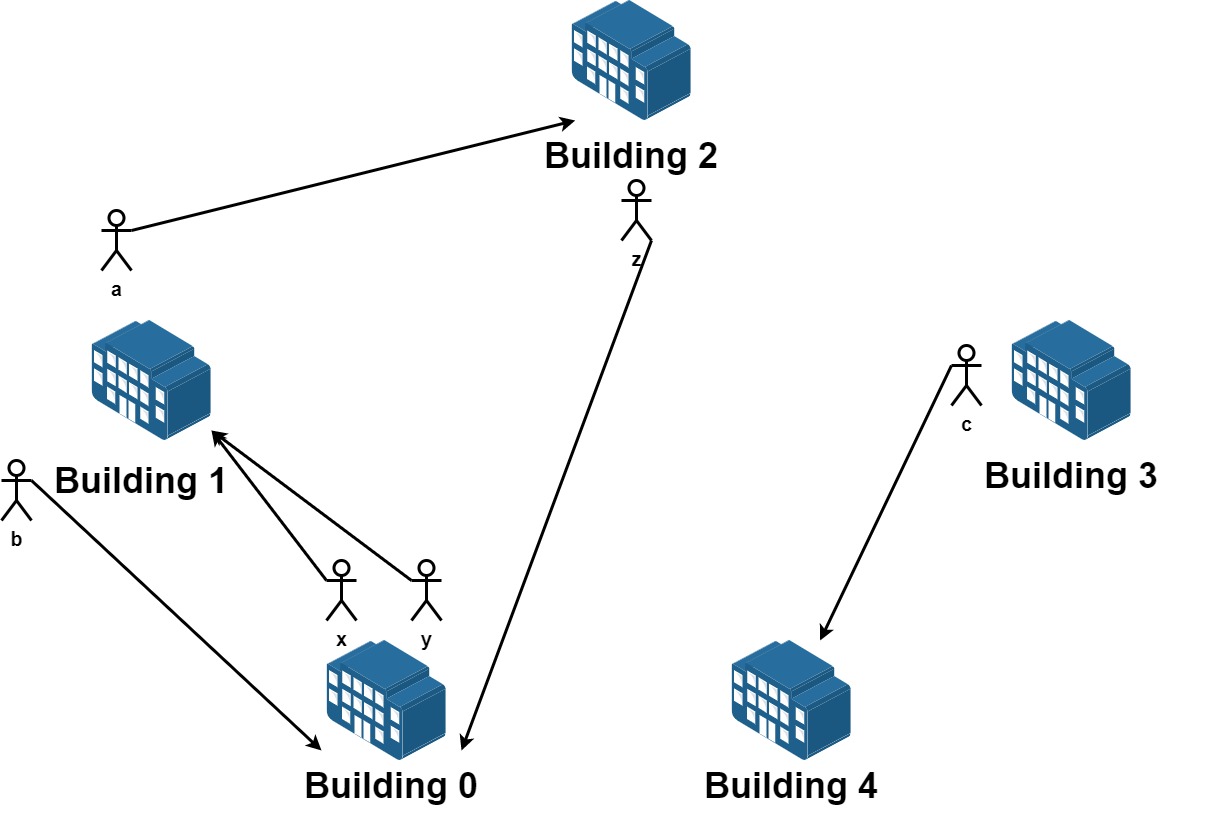
输入：n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出：5
解释：请求列表如下：
从楼 0 离开的员工为 x 和 y ，且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ，且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ，且他想要搬到楼 0 。
从楼 3 离开的员工为 c ，且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼，以满足他们的请求。
我们可以让 y，a 和 z 三人在三栋楼间交换位置，满足他们的要求。
所以最多可以满足 5 个请求。

示例 2：

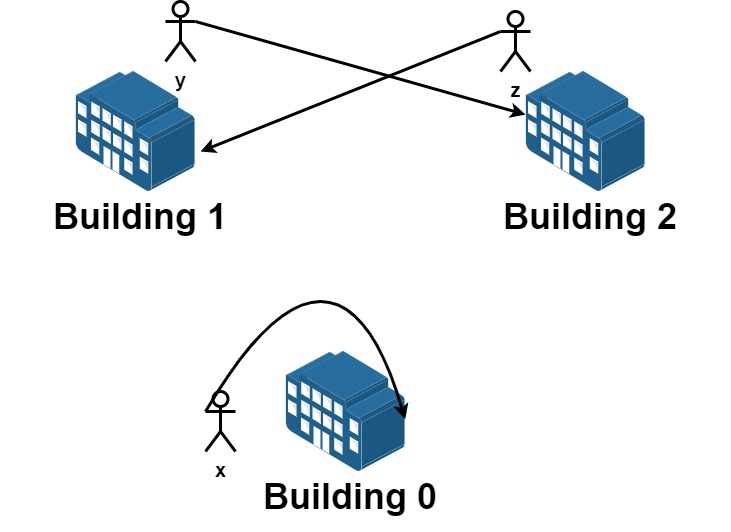
输入：n = 3, requests = [[0,0],[1,2],[2,1]]
输出：3
解释：请求列表如下：
从楼 0 离开的员工为 x ，且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ，且他想要搬到楼 2 。
从楼 2 离开的员工为 z ，且他想要搬到楼 1 。
我们可以满足所有的请求。

示例 3：

输入：n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
输出：4

 

提示：

  • 1 <= n <= 20
  • 1 <= requests.length <= 16
  • requests[i].length == 2
  • 0 <= fromi, toi < n

2、解法1-回溯​

回溯枚举 requests 所有子集，如果所有节点的出度和入度都为0则属于可行的请求列表，取所有可行请求列表的最大长度作为返回结果


3、代码​

var maximumRequests = function (n, requests) {
    let max = 0;
    function backtrace(i, path) {
        const sums = new Array(n).fill(0);
        for (const [f, t] of path) sums[f]--, sums[t]++;
        if (sums.every(s => !s)) max = Math.max(max, path.length);

        for (let j = i + 1; j < requests.length; j++) {
            path.push(requests[j]);
            backtrace(j, path);
            path.pop();
        }
    }

    for (let i = 0; i < requests.length; i++) backtrace(i, [requests[i]]);

    return max;
};

4、执行结果​

image.png


5、解法2-BFS​

BFS 枚举 requests 所有子集，如果所有节点的出度和入度都为0则属于可行的请求列表，取所有可行请求列表的最大长度作为返回结果


6、代码​

var maximumRequests = function (n, requests) {
    let max = 0, queue = requests.map((r) => [r]);
    while (queue.length) {
        const nextQueue = [];
        for (let i = 0; i < queue.length; i++) {
            const reqs = queue[i], sums = new Array(n).fill(0);

            for (const [f, t] of reqs) sums[f]--, sums[t]++;
            if (sums.every((s) => !s)) max = Math.max(max, reqs.length);

            const idx = requests.indexOf(reqs[reqs.length - 1]);
            for (let j = idx + 1; j < requests.length; j++) nextQueue.push([...reqs, requests[j]]);
        }
        queue = nextQueue;
    }
    return max;
};

7、执行结果​

  • 执行用时: 924 ms
  • 内存消耗: 68 MB