1、题干
给定三个字符串 s1、s2、s3,请判断 s3 能不能由 s1 和 s2 交织(交错) 组成。
两个字符串 s 和 t 交织 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
s = s1 + s2 + ... + snt = t1 + t2 + ... + tm|n - m| <= 1- 交织 是
s1 + t1 + s2 + t2 + s3 + t3 + ...或者t1 + s1 + t2 + s2 + t3 + s3 + ...
提示:a + b 意味着字符串 a 和 b 连接。
示例 1:
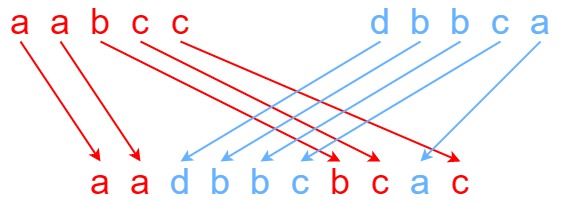
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出:true
示例 2:
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出:false
示例 3:
输入:s1 = "", s2 = "", s3 = ""
输出:true
提示:
0 <= s1.length, s2.length <= 1000 <= s3.length <= 200s1、s2、和s3都由小写英文字母组成
注意:本题与主站 97 题相同: https://leetcode-cn.com/problems/interleaving-string/
遍历解题需要用到3个指针,分别对应字符串
s1、s2、s3。官解说双指针不可行应该只考虑了s1、s2的指针且没有考虑指针重置的情况,实际可以借助指针重置进行解题,详情见解法2。
2、解法1-回溯+记忆化
回溯过程可以理解为同时按字符串 s1、s2、s3 步进,若 s1 当前字符与 s3 当前字符相等则 s1 和 s3 的下标同时加1,若 s2 当前字符与 s3 当前字符相等则 s2 和 s3 的下标同时加1,若最终3个字符串能走到字符串末尾说明结果为 true。
其中记忆化是将已访问过的路径使用哈希集合存储,若后续访问到已访问过的路径,则直接退出当前递归。
3、代码
var isInterleave = function (s1, s2, s3) {
if (s1.length + s2.length !== s3.length) return false;
const visited = new Set();
let res = false;
function backtrace(i1, i2, i3) {
if (i1 === s1.length && i2 === s2.length && i3 === s3.length) return res = true;
if (visited.has(`${i1}-${i2}-${i3}`)) return false;
visited.add(`${i1}-${i2}-${i3}`);
if (s1[i1] === s3[i3]) backtrace(i1 + 1, i2, i3 + 1);
if (s2[i2] === s3[i3]) backtrace(i1, i2 + 1, i3 + 1);
}
backtrace(0, 0, 0);
return res;
};
4、执行结果
5、解法2-三指针+模拟回溯+记忆化
本质上也是回溯+记忆化,只是使用三指针遍历模拟回溯过程,这是个非常规解法随便看看就好。
三指针遍历模拟回溯的大体方案是:遍历 s3,若遇到 s1、s2 都可选的情况则选择 s1,并使用栈存储当前3个指针作为快照;若后续遍历无法继续下去且栈不为空则弹出栈顶快照,重置3个指针并选择 s2 继续遍历;若后续遍历无法继续且栈为空,则结果为 false。
其中记忆化是将已访问过的路径使用哈希集合存储,若后续访问到已访问过的路径则看栈是否为空,栈为空则直接退出当前递归,栈不为空则弹出栈顶快照并重置指针。
6、代码
var isInterleave = function (s1, s2, s3) {
if (s1.length + s2.length !== s3.length) return false;
let i1 = -1, i2 = -1, useStack = false;
const stack = [], visited = new Set();
for (let i = 0; i < s3.length; i++) {
if (s1[i1 + 1] === s3[i] && s2[i2 + 1] === s3[i]) {
if (!useStack) stack.push([i, i1, i2]), i1 += 1;
else i2 += 1, useStack = false;
}
else if (s1[i1 + 1] === s3[i]) i1 += 1;
else if (s2[i2 + 1] === s3[i]) i2 += 1;
else {
if (!stack.length) return false;
[i, i1, i2] = stack.pop(), i -= 1, useStack = true;
continue;
}
if (visited.has(`${i}-${i1}-${i2}`)) {
if (!stack.length) return false;
[i, i1, i2] = stack.pop(), i -= 1, useStack = true;
}
else visited.add(`${i}-${i1}-${i2}`);
}
return true;
};
7、执行结果
- 执行用时: 72 ms
- 内存消耗: 45.4 MB
8、解法3-BFS+去重
这里使用非递归BFS解题,大体思路是:外层遍历字符串 s3,内层遍历当前可选择的所有 s1 和 s2 的下标组合,并且把下一层可选择的所有 s1 和 s2 的下标组合添加到下一层的队列中,如此遍历所有可行组合直至结束,若最终队列不为空则结果为 true。
其中添加下标组合到队列中时一定要去重,否则会超时或内存溢出,去重可以使用双层 map 或者字符串哈希集合。
9、代码
// BFS+双层map去重
var isInterleave = function (s1, s2, s3) {
if (s1.length + s2.length !== s3.length) return false;
let choices = [[-1, -1]];
for (let i = 0; i < s3.length; i++) {
const nextChoices = [], map = {};
for (const [i1, i2] of choices) {
if (s3[i] === s1[i1 + 1] && (!map[i1 + 1] || !map[i1 + 1][i2])) {
nextChoices.push([i1 + 1, i2]);
map[i1 + 1] ? (map[i1 + 1][i2] = 1) : (map[i1 + 1] = { [i2]: 1 });
}
if (s3[i] === s2[i2 + 1] && (!map[i1] || !map[i1][i2 + 1])) {
nextChoices.push([i1, i2 + 1]);
map[i1] ? (map[i1][i2 + 1] = 1) : (map[i1] = { [i2 + 1]: 1 });
}
}
choices = nextChoices;
}
return choices.length > 0;
};
// BFS+字符串哈希集合去重
var isInterleave = function (s1, s2, s3) {
if (s1.length + s2.length !== s3.length) return false;
let choices = [[-1, -1]];
for (let i = 0; i < s3.length; i++) {
const nextChoices = [], set = new Set();
for (const [i1, i2] of choices) {
if (s3[i] === s1[i1 + 1] && !set.has(`${i1 + 1},${i2}`)) {
nextChoices.push([i1 + 1, i2]);
set.add(`${i1 + 1},${i2}`);
}
if (s3[i] === s2[i2 + 1] && !set.has(`${i1},${i2 + 1}`)) {
nextChoices.push([i1, i2 + 1]);
set.add(`${i1},${i2 + 1}`);
}
}
choices = nextChoices;
}
return choices.length > 0;
};
10、执行结果
- 执行用时: 72 ms
- 内存消耗: 48.3 MB
11、解法4-动态规划
官解和其他优秀题解对于动态规划解法已经说得很清楚了,这里就贴下代码和执行结果
12、代码
var isInterleave = function (s1, s2, s3) {
if (s1.length + s2.length !== s3.length) return false;
const dp = new Array(s1.length + 1).fill(0).map(() => new Array(s2.length + 1).fill(true));
for (let i = 1; i < dp.length; i++) dp[i][0] = dp[i - 1][0] && s3[i - 1] === s1[i - 1];
for (let j = 1; j < dp[0].length; j++) dp[0][j] = dp[0][j - 1] && s3[j - 1] === s2[j - 1];
for (let i = 1; i < dp.length; i++) {
for (let j = 1; j < dp[i].length; j++) {
dp[i][j] = (dp[i - 1][j] && s3[i + j - 1] === s1[i - 1]) || (dp[i][j - 1] && s3[i + j - 1] === s2[j - 1]);
}
}
return dp[s1.length][s2.length];
};
13、执行结果
- 执行用时: 92 ms
- 内存消耗: 47.7 MB