1、题干
给你一个数组 pairs ,其中 pairs[i] = [xi, yi] ,并且满足:
pairs中没有重复元素xi < yi
令 ways 为满足下面条件的有根树的方案数:
- 树所包含的所有节点值都在
pairs中。 - 一个数对
[xi, yi]出现在pairs中 当且仅当xi是yi的祖先或者yi是xi的祖先。 - 注意:构造出来的树不一定是二叉树。
两棵树被视为不同的方案当存在至少一个节点在两棵树中有不同的父节点。
请你返回:
- 如果
ways == 0,返回0。 - 如果
ways == 1,返回1。 - 如果
ways > 1,返回2。
一棵 有根树 指的是只有一个根节点的树,所有边都是从根往外的方向。
我们称从根到一个节点路径上的任意一个节点(除去节点本身)都是该节点的 祖先 。根节点没有祖先。
示例 1:
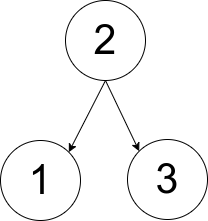
输入:pairs = [[1,2],[2,3]]
输出:1
解释:如上图所示,有且只有一个符合规定的有根树。
示例 2:

输入:pairs = [[1,2],[2,3],[1,3]]
输出:2
解释:有多个符合规定的有根树,其中三个如上图所示。
示例 3:
输入:pairs = [[1,2],[2,3],[2,4],[1,5]]
输出:0
解释:没有符合规定的有根树。
提示:
1 <= pairs.length <= 1051 <= xi < yi <= 500pairs中的元素互不相同。
尽力了,磨了大半天,只想出这么个方法。思路还算清晰,但无法证明解法的正确性,能AC纯粹靠运气。。。
2、解题思路
- 先排除
ways = 0不存在根节点的情况 - 再排除
ways = 0存在互为祖先节点的情况- 如果任意两个节点
a和b不存在祖孙关系,但二者祖孙链上有共同的节点c,则c是a和b的共同祖先 - 若后续能推出
a或b是c的祖先,则说明存在矛盾无法构建树
- 如果任意两个节点
- 再排除
ways = 2的情况:节点存在祖孙关系,且祖孙链长度相同- 补充:任意父节点只有1个子节点都会造成这种情况,此时父子节点可以互换位置构成多棵树
- 剩余情况
ways = 1- 补充:所有父节点都有2个以上子节点才能保证唯一
3、代码
var checkWays = function (pairs) {
const linkDict = [];
const add = (i, j) => {
if (!linkDict[i]) linkDict[i] = new Set();
linkDict[i].add(j);
};
for (const [i, j] of pairs) add(i, j), add(j, i);
const keys = linkDict.map((v, i) => i).filter((v) => v > -1);
keys.sort((a, b) => linkDict[b].size - linkDict[a].size);
// 排除 ways = 0: 不存在根节点
if (linkDict[keys[0]].size !== keys.length - 1) return 0;
// 排除 ways = 0: 存在互为祖先的节点
const ancestorDict = keys.reduce((a, c) => (a[c] = new Set(), a), []);
for (let i = 1; i < keys.length; i++) {
for (let j = i + 1; j < keys.length; j++) {
if (linkDict[keys[i]].has(keys[j])) continue;
for (const li of linkDict[keys[i]]) {
if (li === keys[0] || !linkDict[keys[j]].has(li)) continue;
if (ancestorDict[keys[i]].has(li) || ancestorDict[keys[j]].has(li)) return 0;
ancestorDict[li].add(keys[i]), ancestorDict[li].add(keys[j]);
}
}
}
// 排除 ways = 2: 节点存在祖孙关系,且祖孙链长度相同
for (const [i, j] of pairs) if (linkDict[i].size === linkDict[j].size) return 2;
return 1;
};
4、复杂度
- 时间复杂度:,其中 为节点数
- 空间复杂度:
5、执行结果
