1、题干
如果一棵二叉树满足下述几个条件,则可以称为 奇偶树 :
- 二叉树根节点所在层下标为
0,根的子节点所在层下标为1,根的孙节点所在层下标为2,依此类推。 - 偶数下标 层上的所有节点的值都是 奇 整数,从左到右按顺序 严格递增
- 奇数下标 层上的所有节点的值都是 偶 整数,从左到右按顺序 严格递减
给你二叉树的根节点,如果二叉树为 奇偶树 ,则返回 true ,否则返回 false 。
示例 1:
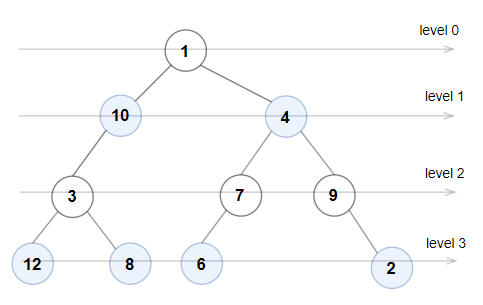
输入:root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
输出:true
解释:每一层的节点值分别是:
0 层:[1]
1 层:[10,4]
2 层:[3,7,9]
3 层:[12,8,6,2]
由于 0 层和 2 层上的节点值都是奇数且严格递增,而 1 层和 3 层上的节点值都是偶数且严格递减,因此这是一棵奇偶树。
示例 2:
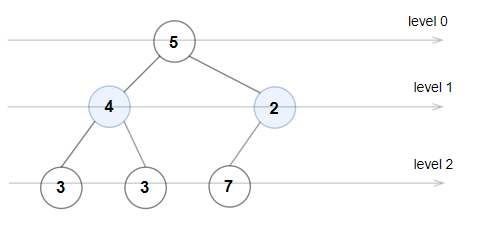
输入:root = [5,4,2,3,3,7]
输出:false
解释:每一层的节点值分别是:
0 层:[5]
1 层:[4,2]
2 层:[3,3,7]
2 层上的节点值不满足严格递增的条件,所以这不是一棵奇偶树。
示例 3:
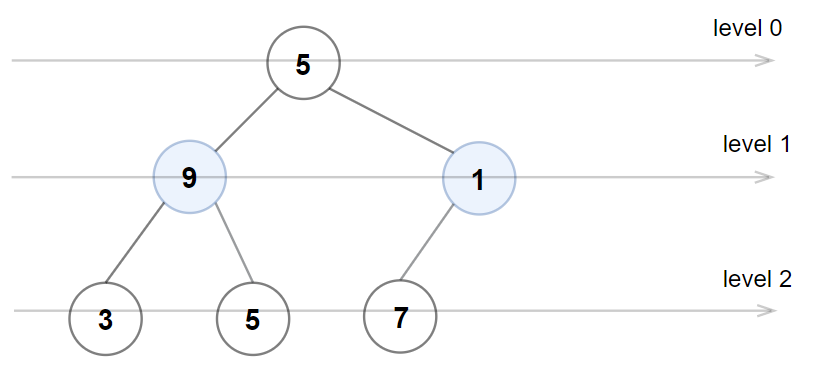
输入:root = [5,9,1,3,5,7]
输出:false
解释:1 层上的节点值应为偶数。
示例 4:
输入:root = [1]
输出:true
示例 5:
输入:root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17]
输出:true
提示:
- 树中节点数在范围
[1, 105]内 1 <= Node.val <= 106
2、解题思路
使用广度优先遍历(BFS)或深度优先遍历(DFS),遍历树上所有节点并判断其是否符合奇偶树的特性。
- 使用广度优先遍历(BFS)时,比较方便做到按层遍历、获取层级和兄弟节点
- 使用深度优先遍历(DFS)时,需要另外使用一个数组存储每层上一次遍历到的节点,用于判断兄弟节点的单调性
3、代码1-DFS递归实现
执行用时:212 ms 内存消耗:82.4 MB
var isEvenOddTree = function (root) {
const nums = [];
function dfs(node, i) {
if (!node) return true;
if (i % 2 && (node.val % 2 || node.val >= nums[i])) return false;
if (!(i % 2) && (!(node.val % 2) || node.val <= nums[i])) return false;
nums[i] = node.val;
return dfs(node.left, i + 1) && dfs(node.right, i + 1);
}
return dfs(root, 0);
};
4、代码2-BFS递归实现
执行用时:308 ms 内存消耗:98 MB
var isEvenOddTree = function (root) {
function bfs(nodes, i) {
const nextArr = [];
for (let j = 0; j < nodes.length; j++) {
if (nodes[j].left) nextArr.push(nodes[j].left);
if (nodes[j].right) nextArr.push(nodes[j].right);
const m1 = i % 2, m2 = nodes[j].val % 2;
if (m1 && (m2 || (j && nodes[j].val >= nodes[j - 1].val))) return false;
if (!m1 && (!m2 || (j && nodes[j].val <= nodes[j - 1].val))) return false;
}
return !nextArr.length ? true : bfs(nextArr, i + 1);
}
return bfs([root], 0);
};
5、代码3-BFS非递归实现
执行用时:276 ms 内存消耗:91.5 MB
var isEvenOddTree = function (root) {
const queue = [[root]];
for (let i = 0; i < queue.length; i++) {
const nextArr = [];
for (let j = 0; j < queue[i].length; j++) {
if (queue[i][j].left) nextArr.push(queue[i][j].left);
if (queue[i][j].right) nextArr.push(queue[i][j].right);
const m1 = i % 2, m2 = queue[i][j].val % 2;
if (m1 && (m2 || (j && queue[i][j].val >= queue[i][j - 1].val))) return false;
if (!m1 && (!m2 || (j && queue[i][j].val <= queue[i][j - 1].val))) return false;
}
if (nextArr.length) queue.push(nextArr);
}
return true;
};
6、执行结果
